基于伏秒平衡原理的Buck－Boost变换器分析

2012-04-26王学梅易根云丘东元

电气电子教学学报 2012年2期

王学梅，易根云，丘东元，张波

(华南理工大学电力学院，广东广州 510640)

Buck-Boost变换器的原理图如图1所示。假设电感电流在整个周期内连续，负载电压Vo的波动忽略不计，视为恒定直流电压。当开关S1导通时，电源Vg向电感供电;当S1关断时，电感电流iL通过D1续流，并向负载供电［7］。

0 引言

Buck-Boost变换器是一种基本的DC-DC变换器，可以实现直流升压和降压功能，在新能源发电领域具有重要的作用。但是现有教材对Buck-Boost变换器分析普遍存在以下不足:①分析方法不统一，只是简单介绍Buck-Boost变换器的工作原理;②只给出电流连续工作模式下输入输出电压关系，未对电流断续工作模式进行分析;③缺乏对Buck-Boost变换器中电量参数的讨论，如未分析电感大小与电流纹波、电容大小与电压纹波之间的关系［1-6］。

为此，本文基于伏秒平衡原理对Buck-Boost变换器进行分析。主要内容包括:①利用伏秒平衡原理及能量守恒原理，分别计算出Buck-Boost变换器在电流连续和电流断续模式下输入输出电压关系;②在此基础上计算电流纹波、电压纹波与电路各参数的关系;③推导电流连续和断续的临界条件，给出整个工作范围内输出电压的定义;④用仿真结果验证了本文分析结果的正确性。

1 伏秒平衡原理

在稳定的Buck-Boost电路中，电感只是储能元件，实现能量的传递，而不消耗能量。在一个电源开关周期T中，电感吸收的能量和放出的能量相等:iL(0)=iL(T)。电感两端电压为

在一个周期T内，电感电压对时间的积分为0，称为伏秒平衡原理。任何稳定拓扑中的电感都是传递能量而不消耗能量，都会满足伏秒平衡原理，Buck-Boost电路中的电感也不例外。

2 变换器的电流连续工作

图1 Buck-Boost变换器的原理图

1) 负载电压的大小

当Buck-Boost变换器工作在电流连续模式(CCM)下，根据伏秒平衡原理，在一个周期内的电感电压平均值为0，则有

由于电感电流在开关管导通期间线性增加，在开关管关断期间线性递减，故电感电流的最大值为IL20，最小值为IL10。则电感电流的纹波大小为

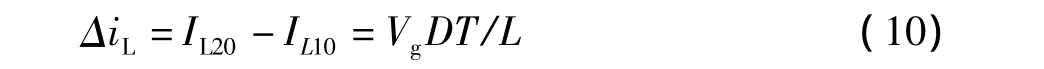
根据能量守恒定律，一个周期内电源向负载提供的能量等于负载在一个周期内消耗的能量，可得

3)电容电流分析

开关管S1导通期间，电源向电感充电，电容C作为恒定电压源为负载R供电，供电电流为ic1。开关管S1关断期间，电感储存的能量释放到负载，一部分用于负载供电，一部分用于电容充电，此阶段电容电流为ic2，其表达式为

4)电容纹波电压分析

由于电容C值有限，负载电压不可能为恒定直流电压，电容两端电压会有微小波动△V，如图2所示［8］。在一个周期内，电容C电荷量最大变化值为

另一方面，电荷量的变化值由电流随时间的积累决定。因此，在Buck-Boost变换器开关管导通期间，电容向负载供电，故电容上的电荷量变化为

图2 电感电流、电容电流及负载电压的波形

3 变换器的电流断续工作情况

1)电感电流分析

当Buck-Boost变换器的电感电流在一个工作周期内出现不连续情况时，被认为工作在断续模式(DCM)。即开关管S1开通前，电感电流已经降为0。即在S1导通期间，电感电流的初始值IL10=0，电感电流的表达式为

其中，tx表示电感电流下降到零的时刻，断续工作模式下电感电流如图3所示。

图3 电流断续工作模式下电感电流的波形

2)负载电压的大小

按照伏秒平衡法则，在一个周期内电感两个端电压平均值为0，故在电流断续工作模式下有

3)临界工作的条件

当tx=T时，Buck-Boost变换器刚好处于电流断续与电流连续之间的临界模式。当tx＜T时，变换器工作在电流断续模式，由式(23)可推出电流断续的工作条件为(2L/RT)＜(1－D)2。

若电路工作的占空比不变，那么增大电感值，可以使电路工作在连续模态;在电路参数不变的情况下，增大占空比也可以使电路工作在连续模态。上述两种措施都是设法增加开关导通期间电感储存的能量。

4 变换器全范围输入输出电压关系

综合以上两种工作模式的分析，可以列出Buck-Boost变换器的全范围输入输出电压关系:

Vo/Vg与D、K的关系如图4所示。其中图4(a)为整个范围内的关系曲线。图4(b)为图4(a)在0≤(Vo/Vg)≤10范围内的放大图，其中的四条曲线分别表示K=0.01，K=0.09，K=0.25 和K≥1的关系曲线。当K≥1时，不管D如何变化，变换器总是工作在电流连续模式。Vo/Vg只与占空比D有关，其大小由式(26a)决定;当K＜1且K＜(1－D)2时，变换器工作在电流断续模式，Vo/Vg由式(26b)决定;当K＜1但K≥(1－D)2时，变换器仍工作在电流连续模式，Vo/Vg由式(26a)决定。以K=0.25为例，当D＜0.5时，K＜(1－D)2，变换器工作在电流断续模式，Vo/Vg=D/;当D≥0.5 时，K≥(1 －D)2，变换器工作在电流连续模式，Vo/Vg=(D/1－D)。