基于AP密度聚类方法的雷达辐射源信号识别

王美玲，张复春，杨承志

（空军航空大学，长春 130022）

0 引 言

雷达辐射源识别是雷达侦察设备的一项基本功能，无论是对战时的敌我识别还是和平时期的电子侦察都起着重要作用，也是实施雷达干扰的基础和前提。随着雷达技术的迅猛发展以及新体制雷达的应用，雷达信号的密度、复杂程度都大幅度提高，传统的识别方法如模式匹配法等对先验知识未知的雷达辐射源无法进行识别，不能适应日益复杂的电磁信号。雷达辐射源信号通常是未知的，而无监督聚类是解决这类问题的有效方法。DBSCAN聚类算法［1］是目前机器学习领域的热点。但是，DBSCAN在处理分布复杂、样本不均匀分布时的识别率较低。其主要原因是该算法在聚类时采用了全局变量，影响了聚类质量。针对DBSCAN算法在处理不均匀样本时识别率较低的缺陷，本文引入亲和传递（AP）算法［2－4］，并将该算法与 DBSCAN 算法结合，以期达到提高识别率的目的。实验表明，新的算法能有效处理不均匀样本，获得较高的正确识别率。

1 DBSCAN算法分析

DBSCAN算法是由Ester Martin等人提出的一种基于密度的空间聚类算法。该算法利用基于密度的聚类概念，即要求聚类空间中一定区域内包含对象（点或其他空间对象）的数目不小于某一给定的阈值。DBSCAN算法具有聚类速度快、有效处理噪声点和发现任意形状空间聚类的优点。

DBSCAN算法的中心思想是：对于某一聚类中的每个对象，在给定半径（文中用Eps表示）的邻域内数据对象个数必须大于某个给定值，也就是说，邻域密度必须超过某一阈值（文中用Minpts表示）。DBSCAN算法的聚类过程基于如下事实：任意两核心点，如它们之间的距离在Eps内，则将它们放入一类中；类似地，与核心点的距离足够近的边界点也放入核心点相同的类中，丢弃噪音点。

1.1 相关概念

DBSCAN相关的一些定义：

定义1：x是给定数据集D中的一个对象，x的Eps邻域定义为：NEps＝ ｛y∈D｜d（x，y）≤Eps｝。

定义2：如果一个对象的邻域中至少包含Minpts个对象，就称这个对象为核心对象。

定义3：对于一个给定对象，如果它属于某个核心点的近邻而自己本身不是核心点，那么称它为边界点，如图1所示。

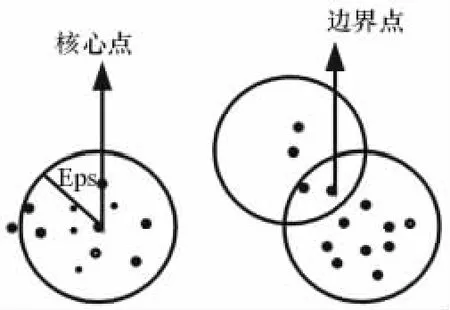
图1 核心点和边界点

定义4：如果p是一个核心对象，p在q的邻域Eps中，称p是从直接密度可达的。

定义5：如果存在一个对象链p1，p2，…，p n，其中p1＝p，p n＝q，且满足p i从p i＋1直接密度可达，则称对象p是从对象q关于Eps和Minpts密度可达。

定义6：如果对象集合D中存在一个对象o，使得对象p和q是从关于Eps和Minpts密度可达的，那么对象p和q是关于Eps和Minpts密度相连的。

1.2 聚类过程

DBSCAN算法的详细步骤：

（1）将所有点分类，分别标记为核心点、边界点或噪音点；

（2）删除噪音点；

（3）连接距离在Eps内的所有核心点；

（4）将之间存在的连接的核心点放入同一类中；

（5）将边界点分入与之相应的核心点所在类中。

虽然DBSCAN算法有聚类速度快、能够有效处理噪声点和发现任意形状的空间聚类的优点，但是该算法无法同时聚类不同密度的簇，这是因为它对于一个数据集只选取统一的Eps和Minpts。在实际情况下，簇的密度虽然不同，但具有一定的相同意义，这种情况在辐射源识别问题中很容易造成增批现象。

2 AP聚类算法分析

2.1 算法思想

亲和传递（AP）聚类是由Frey等人于2007年在Science上提出的一种新的无监督聚类算法。亲和传递聚类算法的快速、有效性体现在处理大数据集的聚类问题上，例如对数千个手写邮政编码的图片，该算法只花费了5 min就可以找出能准确解释各种笔迹类型的少量图片，而K均值算法在同样的时间内达到的精度却很低。

AP算法将所有的数据点看成潜在的聚类中心点，这样就避免了聚类结果受限于初始类代表点的选择。在AP聚类中，假设把每个数据点都看作是有向图中的一个节点，任意节点之间传递责任度和可用度2种信息，在该图的有向途径上不断递归地传送这2种信息并修改它们的值，直到一个适合的类代表点和相应的聚类出现，如图2所示。

2.2 AP算法的过程

AP算法首先建立一个N×N相似度关系矩阵S作为工作基础，此相似度矩阵是由N个数据点之间的相似度组成的。本文使用负的欧氏距离平方来计算任意两点之间的相似度，如S（i，j）＝－｜｜x iy j｜｜2，其范围在（－∞，0］。相似度矩阵S就是由这些相似度组成的N×N阶矩阵。在循环迭代过程中，各样本点竞争最终的聚类中心。

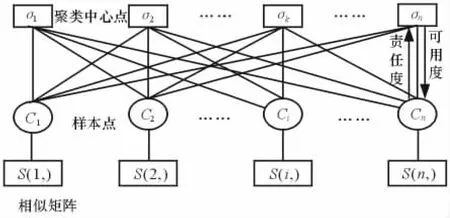
图2 AP算法主要思想

在循环迭代中，若一个数据点x k处于其相邻数据点的中心位置上，则该点与其它数据点的相似度之和较大，即s（i，k）之和较大，将它作为类代表点的可能性也就较大。反之，处于聚类边缘的数据点与其它数据点的相似度之和）较小，成为聚类中心的可能性也越小。聚类之前，AP算法中需预先设定的偏向参数p（k）作为样本点k被选作聚类中心的倾向性。

通常在没有先验知识的情况下，笔者认为每个数据点的偏向参数都应取相同的值，一般取相似度矩阵S的中值作为偏向参数p的初始值，即设定所有偏向参数p（k）为相同值p。同样，p值的大小也影响到最终得到聚类的类的个数。AP算法可以通过改变p值来寻找合适的类的数目，一般情况下，减小p值可以减少类的个数，增大p值可以增加类的个数，p是AP算法的一个重要参数。

AP算法任意2个数据点之间传递着2种类型的消息，分别为责任度矩阵R＝［r（i，k）］n×n和可用度矩阵A＝［a（i，k）］n×n。这2个信息量代表了不同的竞争目的，r（i，k）是从点x i指向点x k，它代表点x k积累的能量，用来表示数据点x k适合作为数据点x i的类代表点的代表程度。

a（i，k）是从点x k指向点x i，它代表点x i积累的能量，用来表示数据点x i选择数据点x k作为类代表点的合适程度。对于任何数据点x i，计算所有数据点的代表程度r（i，k）和a（i，k）之和。r（i，k）与a（i，k）的和越大，则k点作为聚类中心的可能性就越大。AP算法的核心步骤为2个信息量的迭代更新过程。下面是责任度R与可用度A的计算公式［6］：

AP算法在信息更新这一步骤引入了另外一个重要的参数λ，即阻尼因子。它作为平衡因子，对上一次迭代和本次迭代的责任度和可用度进行加权计算，得到本次迭代最终的相似度和可用度。平衡因子主要有2个作用：影响AP聚类迭代的平稳性；当迭代的次数一定时，迭代循环发生振荡不能收敛，可以增大阻尼因子使算法收敛。另外，当算法产生的类数过多时，也可以增大阻尼因子。设当前迭代次数为i，加权公式为：

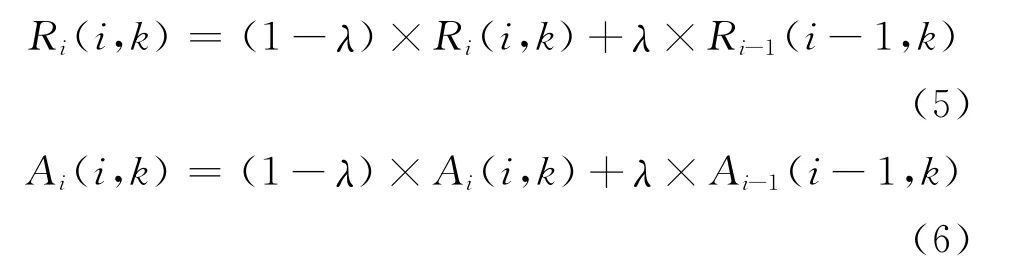
其中λ∈［0，1）阻尼因子的作用是避免AP算法发生振荡，增大阻尼因子可以消除振荡。在本文的实验中，为了避免振荡的发生，设置阻尼因子为0.9。

AP聚类相对K－Means聚类的改进之处在于：AP聚类克服了K－Means聚类方法的一些缺点：对初始聚类中心的选择极为敏感且容易陷入局部极值。在其迭代过程中不断地搜索适合的聚类中心，使得聚类目标函数最大化。

经过聚类后的数据变成了小样本，减少了计算量，保证了系统实验具有可行性。所以该算法可以不必事先指定聚类的数据，有助于解决未知雷达辐射源信号的识别处理问题。

但是由于AP算法也是基于中心的聚类算法，因此它也像其它中心算法一样，不适应非凸形分布的数据聚类，且由于它的聚类中心是实际数据，并非可移动的虚拟中心，因此只能实现小范围聚类。实验证明，将AP聚类算法用于信号识别会产生较严重的增批现象，因此需要对AP算法聚类结果再进行聚类处理，以达到更理想的效果。

3 基于AP密度聚类的雷达辐射源信号识别算法

3.1 基于AP密度聚类算法流程

本文将AP聚类与改进后的DBSCAN算法结合，设计了适合未知雷达辐射源信号的识别算法，即基于AP密度算法。具体实现流程如图3所示。

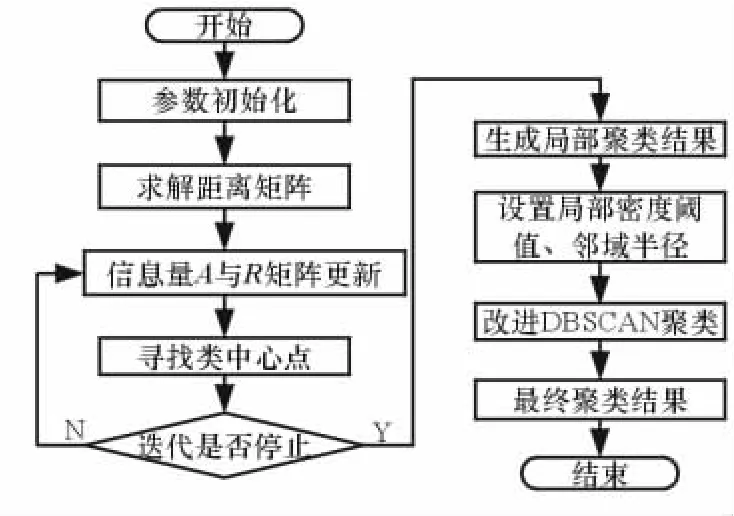
图3 基于AP密度算法流程图

3.2 基于AP密度聚类分选实现步骤

基于AP密度聚类分选的输入是归一化之后的脉冲描述字（PDW）特征参数，对PDW的信号分选处理过程如下：

（1）设置初始聚类参数。初始聚类参数有迭代数目、代表矩阵、适应矩阵、阻尼因子和噪声阈值。

（2）设输入的归一化［7］PDW 特征参数矩阵含有n条待聚类的PDW特征参数（称为样本），即：

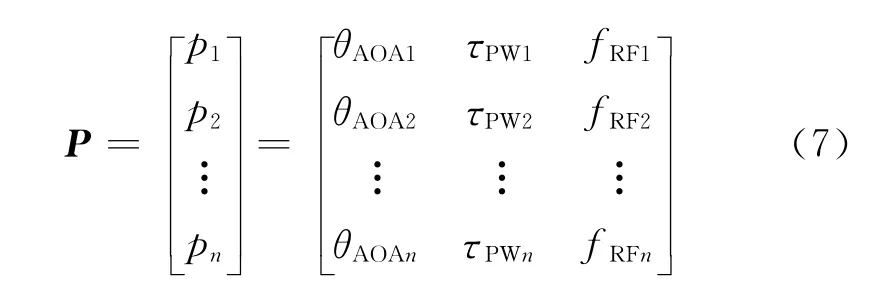
式中：P为待分选的雷达信号特征参数矩阵；p i为一条PDW数据；θAOAi为第i个脉冲的到达角；τPWi为第i个脉冲的脉宽；fRFi为第i个脉冲的载频。

（3）求解距离矩阵，得出相似矩阵，设置相似度矩阵对角线元素s（k，k）为矩阵的中值。

（4）进行信息更新，找到每个数据点的类中心点，若满足以下迭代条件中任意一个，迭代过程则结束：

（a）满足迭代次数；

（b）信息改变量低于阈值；

（c）选择的类中心值在连续几次迭代中保持稳定。

（5）生成局部聚类结果，获得聚类与类代表点。（6）设置局部密度聚类阈值、邻域半径。

（7）运用DBSCAN算法对AP聚类结果进行再次聚类。

（8）输出最终聚类结果。

3.3 识别算法仿真实验及性能分析

为了验证基于AP密度聚类算法对未知雷达辐射源信号识别的有效性，本节利用生成的PDW信号进行基于AP密度聚类算法的仿真实验。

为了验证本文算法的准确性，对算法进行了仿真试验，并将本算法与文献［8］中提出的基于KMeans的改进算法及DBSCAN算法进行了比较。

为了体现雷达信号环境的复杂性、交错性与数据真实性，本实验查阅了机载和舰船雷达手册，并结合前线真实数据，模拟了6部雷达信号数据，并设置了贴近实际的信号参数。雷达信号的频域、时域、空域参数的变化形式是影响信号分选算法的主要因素，依据雷达手册对相应雷达辐射源的PDW参数变化形式进行典型设置，如表1所示。

表1 仿真雷达辐射源参数信息表

从图4～图6和表2中可以看出，本文提出的基于AP密度算法成功将所有雷达信号识别出来，体现了较高的准确性。

改进的K－Means方法对第1部雷达进行识别时产生了增批现象，这说明虽然对原算法进行了改进，但是由于算法本身的限制，对于非凸形的信号分布仍然不能很好地进行正确分选；基于密度的聚类算法由于采用全局性参数，对第2部雷达进行识别时出现了漏选情况。

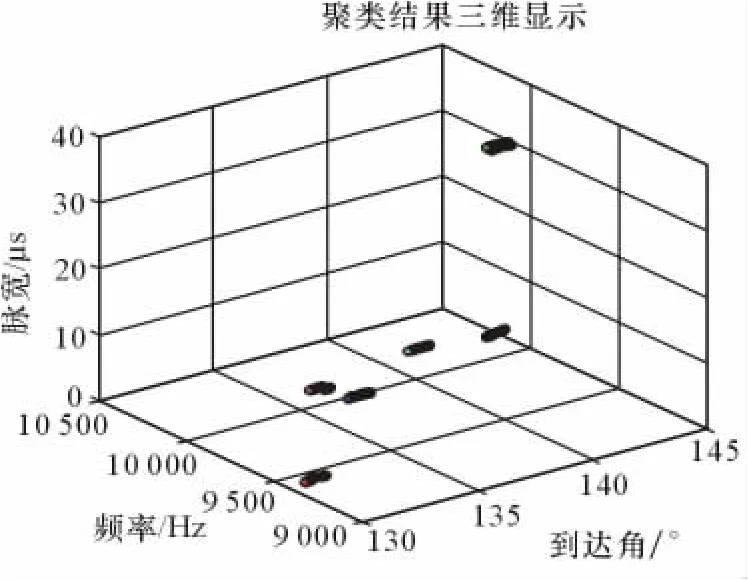
图4 改进K－Means聚类结果

图5 DBSCAN聚类结果

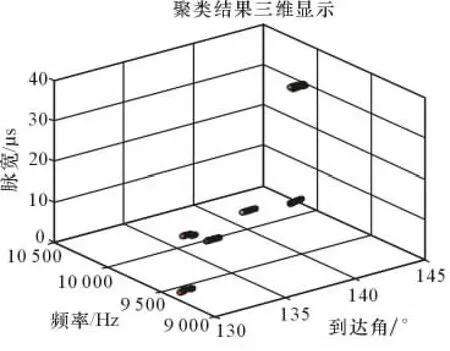
图6 基于AP密度聚类结果

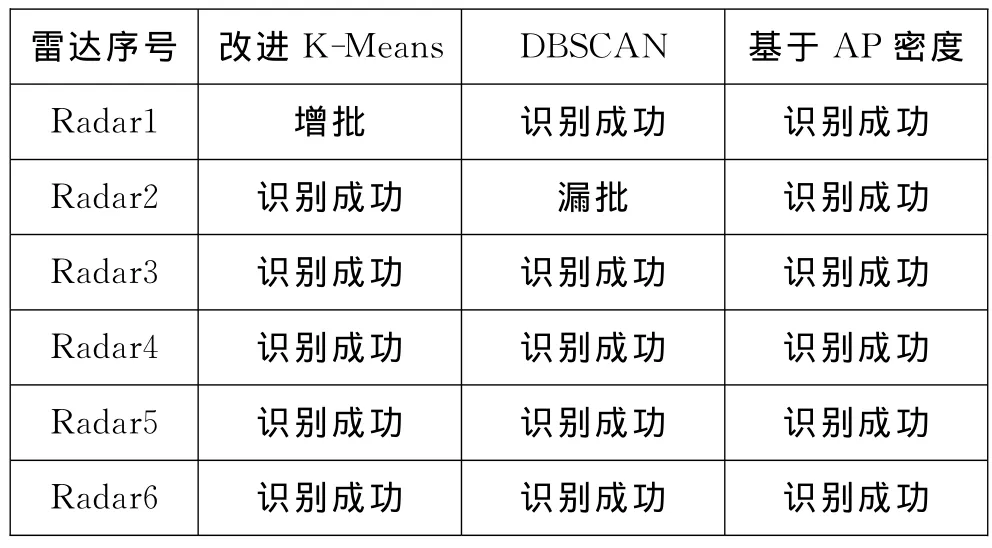
表2 算法结果比较

4 结束语

本文在分析了AP聚类及DBSCAN聚类的基础上，提出了一种基于基于AP密度聚类的未知雷达辐射源信号识别算法。该方法在一定程度上克服了AP聚类及DBSCAN聚类的局限，提高了算法的识别率，具有一定的推广价值。

［1］陈峰.基于聚类的增量数据挖掘研究［D］.大连：大连海事大学，2007：27－34.

［2］Frey B J，Delbert Dueck.Clustering by passing messages between data points［J］.Science，2007（315）：972－976.

［3］Givoni I E，Frey B J.A binary variable model for affinity propagation［J］.Neural Computation，2009，21（6）：1589－1600.

［4］Dueck D，Frey B J，Jojic N.Constructing treatment portfolios using affinity propagation［A］.Proceeding of 12th Annual International Conference，RECOMB 2008［C］.Singapore，2008：360－371.

［5］肖宇，于剑.基于近邻传播算法的半监督聚类［J］.软件学报，2007，19（11）：197－199.

［6］王慧，申石磊.一种改进的特征加权K－means聚类算法［J］.微电子学与计算机，2010，27（7）：161－163.

［7］孙鑫，侯慧群，杨承志.基于改进K－均值分类的未知信号分选方法［J］.现代电子技术，2010，17（2）：91－93.