渡河问题的图解分析
2012-04-24温鸿航温鸿翔任晓莉
温鸿航,温鸿翔,任晓莉
(1.西安电子科技大学通信工程学院,陕西西安 710071;2.陕西广电网络(集团)有限公司,陕西西安 710075;3.西安交通大学城市学院,陕西西安 710018)
“渡河问题”作为人们熟知的经典趣味性智力题目之一,在各种智能训练、测试和数学建模比赛中常会遇到[1]。而对其进行较为深入的一般性系统讨论尚不多见。文献[2]虽对此作了较详细的讨论,给出了应用计算机进行智能求解的方法;但该方法对数学要求较高,不利于教学普及。见于此,文中在文献[1]的启发下,应用简单直观的图解法对渡河问题作初步探讨,以期为编拟该类智能题目提供参考依据以及求解的思路。
1 渡河问题两种常见的描述
为利于今后讨论的一致性,先将渡河问题简述如下(括号内的“或m”、”或n”用于作一般性讨论时来替代前面的具体数字):
问题1 传教士与食人族渡河问题。
在河流的左岸现有3位(或m位)传教士和3个(或m个)食人族,他们欲利用左岸边最多可乘坐2人(或n人)的小舟渡到河右岸去。假设每个人都会划船;其限制是:无论是在左岸、船上还是右岸的场合下,都不得出现食人族人数多于传教士数目的不安全情况,因这样可能发生食人族攻击传教士的危险。
问题2 阿拉伯夫妇渡河问题。
即有3对阿拉伯夫妇欲利用能载客2人的小船从河左岸过渡到右岸去,已知每个人都会划船。其限制是:按照习俗任一位妻子都不得在其丈夫不在场陪伴的场合下与别的男子碰面。
上述表述中各有两个限制(约束条件):
(1)小船的载运能力n(运能约束),即在往返摆渡过程中船上乘员最多不超过n;(2)两岸三处人员组成的限制(组合约束)。下面就约束条件进行讨论。
前述对渡河问题的两种表述,其约束条件(1)相同;而从字面看似乎两种表述的约束条件(2)不同;但实际上,问题2的限制与问题1并无较大差异,对于2中的人员组合的限制,可以理解为:在各种场合下都不能出现女子人数多于男子数的情况。假如在某一侧岸边出现了女多于男的情形,则必然有一位女性的丈夫是不在现场、而现场又是有别的男性在场的,这当然是不合礼俗规定的。对渡河问题的以上两种表述其唯一差异点在于:问题1中的2 m个两类元素传教士与食人族之间不存在任何对应关系,若设过渡过程中某个时刻在两岸中任一场合的人员组合状态是由x个传教士与y个食人族组成的,那么只要在人数上符合人员组合约束条件(2),即

则不论是哪位(或哪几位)传教士与哪(几)位食人族在一起都是合法的,即其组合对于两种元素成分没有选择匹配的要求,在同一类成员中的各个元素是没有区别而平等存在的;这样在构成某种状态组合时只需注意满足组成人员数目上的限制即可,而无需对同类元素的个体进行选择,故约束条件是较为宽松的。而问题2的约束(2)显然要更为严苛一些,因为男子集合中每一个个体与女性集合中的某个指定个体有着对偶匹配关系,故在渡河过程的每个状态下除了需满足前述对于任一组合中两类人员人数的约束(2)之外,还须在两岸三处的人员组合中进行指定性的选择安排,即考虑两类成员男女之间的配偶对应关系。不过这种礼俗上的约束符合人之常情,在具体实施中稍加注意即可满足;为简单起见,文中略去了问题2中两类元素集合中个体的差异性,将问题2合并于问题1一起进行讨论。此后的论述中若无特别说明时将只就问题1展开,并认为其中亦包括了对问题2的讨论与求解。
2 状态坐标点及其迁移
仿照整数(二元)规划的图示方法,因构成渡河问题的元素只有两种——传教士与食人族,即在问题求解过程中某一时刻河岸上的人员组合状态Sk,包含初始状态S0与最终状态SK=G,都可以用二维坐标点Sk(x,y)来表示;这里x和y分别为河岸某一侧传教士和食人族的人数。显然x、y均为整数且有0≤x,y≤m;具体在m=3,n=2的问题中应是0≤x,y≤3。下标k=0,1,2,…,K,表示经过K次摆渡后问题获得解决,亦即实现了“始点S0→目标G(=SK)”的状态迁移。摆渡次序k的计算是按照每个单趟运载算作一次,即小船往返一个来回按两次计。对于同一题目,在有多种解法时,当然总步数K应为所有可行路径中的最短路径,且K必为奇数。
2.1 滞留左岸的人员组合状态
滞留左岸的人员组合状态,如图1(a)所示,设置直角坐标系O—xy;在m=3时共有(m+1)2=42=16个交点:(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),…,(3,3),亦即16个可能状态点。若着眼于用左岸(即出发一侧)滞留人员的组合来表征问题求解过程中人员变动的态势时,那么渡河问题的解决就是使得滞留于左岸的人员组合——(传教士人数x,食人族人数y)=Sk(x,y),由始点 S0=(3,3)出发,在约束条件下经K次摆渡后迁移至目标点SK=(0,0)=G(与坐标原点O重合)。其求解过程如图1(a)所示。显然,凡是使得Sk(x,y)的坐标值下降的坐标点迁移,即表示由左岸的初始状态 S0(3,3)向着最终的目标点G(xK,yK)=O(0,0)前进,亦即代表从左岸向右岸渡去的行程;文中把这种使问题趋于解决的行程(左岸→右岸)称之为“正行程”,包括使x减小、或使y减小、或者x和y同时减小的坐标迁移。而在每次正行程之后(除最后一次正行程已经达到目标状态),紧接着必然有一次使小船返回左岸的“回程”(使x增大、或使y增大、或者使x和y同时增大的坐标迁移,图中用虚线箭头表示),以便继续实施下一次“左岸→右岸”的正行程摆渡,直到K=11时完成全部摆渡任务。图1(a)的解路径可简单表示为(实线箭头表示正行程,虚线表示回程)
左岸 S0=(3,3)→(3,1)﹍(3,2)→(3,0)﹍(3,1)→(1,1)﹍(2,2)→(0,2)﹍(0,3)→(0,1)﹍(0,2)→(0,0)=G
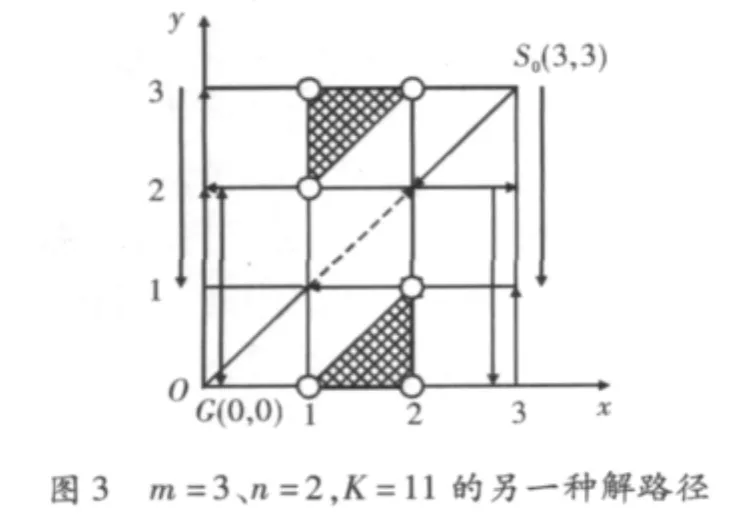
若从提高完成任务的运载效率考虑,由常识可以定性地认为:在每一次正行程中应尽量增大乘船人数,充分利用运载能力n,以图用尽量少的摆渡次数K达成目标;而在回程则应尽量减少船上的乘员数目,以减小无谓的消耗。特别是在运载成本极其重要的情况下,或是在一题多解(即对于相同的m和n,有一个以上总摆渡次数同为K而路径不同的解决方案,如图3所示,时需要对不同的解路径作出评价比较的场合下,当然就需要对运载效率或者解路径的经济性作定量的分析计算。

图1 坐标迁移解路径
2.2 右岸的人员组合状态
图1(a)是以滞留于左岸的人员组合状态Sk(x,y)为对象来进行求解的;当然也可以以到达右岸的人员组合状态为对象进行求解。为与左岸相区别,这时将坐标系设为O'—x'y',右岸的初始状态为S'0(0,0),目标状态为S'K'(x',y')=G'(3,3)。由于此时的始点S'0与坐标原点O'重合,而目标点G'则在距离原点最远处;故与前述左岸的情形恰好相反,这时的“正行程”应为坐标值增大的方向,“回程”则在向坐标原点收缩靠拢的方向上。为方便后面对坐标点的分类分析中与图1(a)相对照,这里将O'—x'y'坐标系作了逆时针180°旋转,这并不影响问题的求解过程。由图1(b)可知,经过K'=11次的坐标迁移后,右岸将达到目标状态G'(3,3);这一结果与前述关注左岸滞留人员组合状态(图1(a))时的结果K=11相一致,这是预料之中的,因为二者仅仅是对河岸上人员状态的着眼点由左岸变换为右岸而已,并未对其路径或过程作任何变化。同样可将关注右岸人员组合时的解路径(图1(b))简记为
右岸 S0'=(0,0)→(0,2)﹍(0,1)→(0,3)﹍(0,2)→(2,2)﹍(1,1)→(3,1)﹍(3,0)→(3,2)﹍(3,1)→(3,3)=G
3 状态坐标点的分类
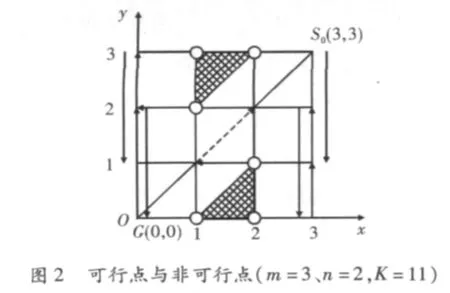
在图1(a)中,当从始点S0(3,3)出发,在探寻逐步趋向目标点G(0,0)的最短路径的过程中,必须对每一个正行程的落脚点和随后的回程落脚点其坐标是否满足组合约束条件(2)进行判断。为此,这里试图在搜索求解之前就对所有的(m+1)2个可能状态点进行分析归类,标出那些不符合约束条件的状态点——称作“非可行点”,从而使得搜索求解中能够避免误入这些违反约束的“禁区”。
由图1(a)可知,点(1,2)、(1,3)、(2,3)显然是非可行点(用⊙表示),因为这些点所表示的左岸滞留人员组合都是x(传教士人数)<y(食人族人数)的状态,是不符合约束条件(2)的。
为便于解释另外3个非可行点(图1(a)中用*标示)——(2,1)、(2,0)、(1,0),需要与图 1(b)相对照;因为这3个点表面上似乎是满足组合约束条件(2)的,即符合0<x≤3且x≥y;但是实际上它们是非可行点。因为组合约束条件(2)是要求在两岸三处都得到满足。而此3个状态点虽然在左岸满足了组合约束,但在对应的右岸却是不满足组合约束的。这一点只要对照图1(a)和图1(b)即可知道。图1(b)所示的右岸状态迁移过程中,在点 S'(x',y')=(1,2)、(1,3)、(2,3)处显然不满足x'≥y',即为非可行点(同样用⊙表示)。假想图1(b)是绘制在透明胶片上的,就可以将其移动到与图1(a)相重叠的位置,使得两个图上左右两岸的始点 S0(3,3)→S0'(0,0)、目标点 G(0,0)→G'(3,3)分别对准,成为相互影射关系;则易于发现图1(a)与图1(b)上的求解路径确是相互重合的。这意味着不论关注的是左岸还是右岸现有人员的组合态势,这时其求解路径是相同的(这是就此实例所作的推断,而在一题多解的场合则不能这么简单地推断。为说明这一点,对于m=3、n=2给出了不同于图1(a),图1(b)的另一条解路径如图3所示,其求解步数则与图1相同,仍为K=11)。那么与右岸的3个非可行点(x',y')=(1,2)、(1,3)、(2,3)相对应的左图 1(a)中的影射点(x,y)=(2,1)、(2,0)(1,0)也应是非可行点。同样地可以判定,与图1(a)中3个非可行点(x,y)=(1,2)、(1,3)、(2,3)相对应的图 1(b)中 3 个影射点(x',y')=(2,1)、(2,0)、(1,0)也是非可行点。据此可知,无论是着眼于左岸状态还是右岸状态,都有着6个非可行点;现将这6个非可行点合并表示于图2中。为给后续求解过程中的图搜索提供导引信息,文中将对角线以上的非可行点所构成的三角形区域称作“上禁区”(图中网格部分,下同),对角线以下的非可行点三角形区域称作“下禁区”,即在坐标迁移(或图搜索)过程中应避免在该区域停留,但可以飞越。
在剔除了上述非可行点之后,当然余下的就是可行点。具体来说,这里共有10个可行点:
(1)直线 x=m=3 上的(3,0)、(3,1)(3,2)及S0(3,3),共4 个点;
(2)直线 x=0(即 y轴)上的 G(0,0)、(0,1)、(0,2)、(0,3),共4 个点;
(3)过原点的 45°对角线上的点(1,1)、(2,2),共2个点;始点S0(3,3)和目标点G(0,0)已包括在上两项中,故不再重复计入;以上3项总计10个可行点。
若进一步细分,还可以在这些可行点的集合中把对角线上的点特别地称作“平衡点”,因为在这些点上始终满足x=y(或者x'=y'),亦即两类构成元素——传教士与食人族是势均力敌的,这种场合下便不会发生在此岸可行而在彼岸不可行的矛盾。平衡点的引入对于应用计算机图搜索技术将是有益的。
以上是就m=3、n=2的具体事例的分析。推广到一般情况下(即:有m个传教士与m个食人族利用最多能载n个人的小船欲从河流左岸过渡到右岸去),这时可以在求解问题之前由如下各式对图搜索的范围做到心中有数。
(1)可能状态点数

(2)可行点数:直线x=0和x=m上各有(m+1)个,对角线上有[(m+1)-2]个,故可行点总数为

(3)非可行点数

依据上述各式,表1中列举出一些简单m时的各类对应点数,以及使问题得以成立而所需nmin、对应的K值,以供参考。

表1 可行点数、不可行点数以及最小运能nmin
以上各式中均未出现小船运载能力参数n,即表明可行点数(或非可行点数)仅仅取决于欲渡人员数m(双)而与n无关。但n的大小显然会影响到完成任务的摆渡总次数K,亦即问题求解的难易程度;对于相同的m值,若n越大则所需的摆渡次数K越小(例如对于m=3而言,当n=2时K=11,当n=3时K=5),问题求解就愈简单;反之亦然。本文认为,一般在编拟此类智力题目时应有限制nmax=m,因为这种情况下总有K=5的最短求解路径存在,问题求解已经变得很简单了,进一步的简单化(即继续增大运能n)也就失去了智力训练和测试的意义了。至于运载能力的下限nmin的存在是显而易见的,至少也应有n≥2,才有可能使得往返摆渡(即正行程+回程+正行程+…)能够连续进展下去,否则将无解(若运载能力n=1,则正行程与随后的回程在小船上最多和最少都只有一人,一个往返航程的实际摆渡效果为0人,即不可能完成渡河任务);但由于nmin是与m值有关的,要比nmax复杂些,故此处仅作提示而留待后续再作进一步讨论。
4 结束语
作为趣味智力训练和测试的经典题目,在以往的求解中多是用脑体操的逻辑推理方式来解决的,系统深入的探讨较少。这在所处理的数值较小、问题较简单时是能解决问题的。但考虑到此类问题在规划、管理等领域可能存在的潜在应用及在较大数值条件下求解的复杂性,文中尝试用图解法来表示问题求解路径中状态点的变迁,并对状态坐标点作了分类分析,对此类题目的编拟给出了一些初步建议;以期为探寻此类问题的简便求解思路创造条件。
[1] 周义仓,赫孝良.数学建模实验[M].西安:西安交通大学出版社,1999.
[2] 武藤佳恭,ニュ-ラル コンビュ-ティンゲ[M].東京,コロナ社,1996.
[3] 邓兴无.滑动摩擦平衡问题的图解分析法[J].电子科技大学学报,1997(S1):281-284.
[4] 田社平,陈洪亮.含运算放大器电路的图解分析[J].电气电子教学学报,2012(2):92-94,106.
