日晕轨道卫星的转移轨道中途修正研究
2012-04-17胡少春孙承启刘一武
胡少春,孙承启,刘一武
(1.北京控制工程研究所,北京 100190;2.空间智能控制技术重点实验室,北京 100190)
由于平动点任务探测器对转移轨道初始误差(指离开地球停泊轨道)的敏感性、发射过程中不可避免地存在误差以及各种摄动因素的影响,因此必须考虑转移轨道的中途修正问题.通常,向晕轨道的转移时间较长,必须进行多次中途修正.文献[1-2]考虑误差过于简单,假设只存在初始发射偏差,而忽略了导航误差和中途修正引入的修正偏差等.文献[3]给出了一种定时闭环修正策略,但其忽略了导航误差和初始发射时间误差.文献[4]给出的算法修正次数多,且忽略了初始发射位置误差和时间误差.此外,现有平动点转移轨道中途修正的文献并未研究地球引力摄动、月球引力摄动和太阳光压摄动等摄动因素对修正代价和修正效果的影响.
本文主要进行初始发射误差的灵敏度分析,讨论误差源和摄动因素对转移轨道修正代价和修正效果的影响,研究考虑多种误差源和摄动因素的中途修正策略.本文选择Az振幅为120000km的目标晕轨道,以晕轨道近地点入轨的转移轨道为例进行中途修正的研究.
1 初始发射误差的灵敏度分析
由于卫星从地球飞向日晕轨道需要100多天,因此,即便是很小的误差,如不进行修正,卫星也不能正确进入晕轨道.
1.1 初始发射位置误差
若初始发射位置误差为1km,则转移轨道如图1所示.可见,尽管初始误差很小,但不加控制的转移轨道会逐渐偏离标称转移轨道.
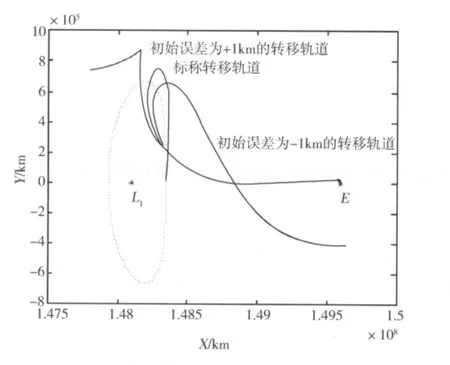
图1 标称转移轨道与存在初始位置误差的转移轨道Fig.1 Nominal transfer trajectory and transfer trajectory with initial launch position error
初始发射误差为1km时,在发射后不同时刻修正所需要的修正量如图2所示.可以看出,在初始发射误差给定的情况下,修正时刻越晚,所需的修正量越大.由此可见,第一次修正越早越好.

图2 修正量与修正时刻的关系Fig.2 Relation between correction maneuvers and correction times
不同初始发射位置误差在发射后1天末修正所需的修正量如图3所示.由图可见,修正量和误差量成正比.

图3 修正量与初始发射位置误差的关系Fig.3 Relation between correction maneuvers and initial launch position errors
1.2 初始发射速度误差
假设初始发射速度误差沿卫星实际运动方向,若初始发射速度误差为1m/s,则转移轨道如图4所示.可见,初始速度误差对转移轨道的影响也很大.

图4 标称转移轨道与存在初始速度误差的转移轨道Fig.4 Nominal transfer trajectory and transfer trajectory with initial launch velocity error
初始发射速度误差为1m/s时,在发射后不同时刻修正所需要的速度增量如图5所示.可以看出,在初始发射误差给定的情况下,修正时刻越晚,所需的修正量越大.可见,第一次修正越早越好.
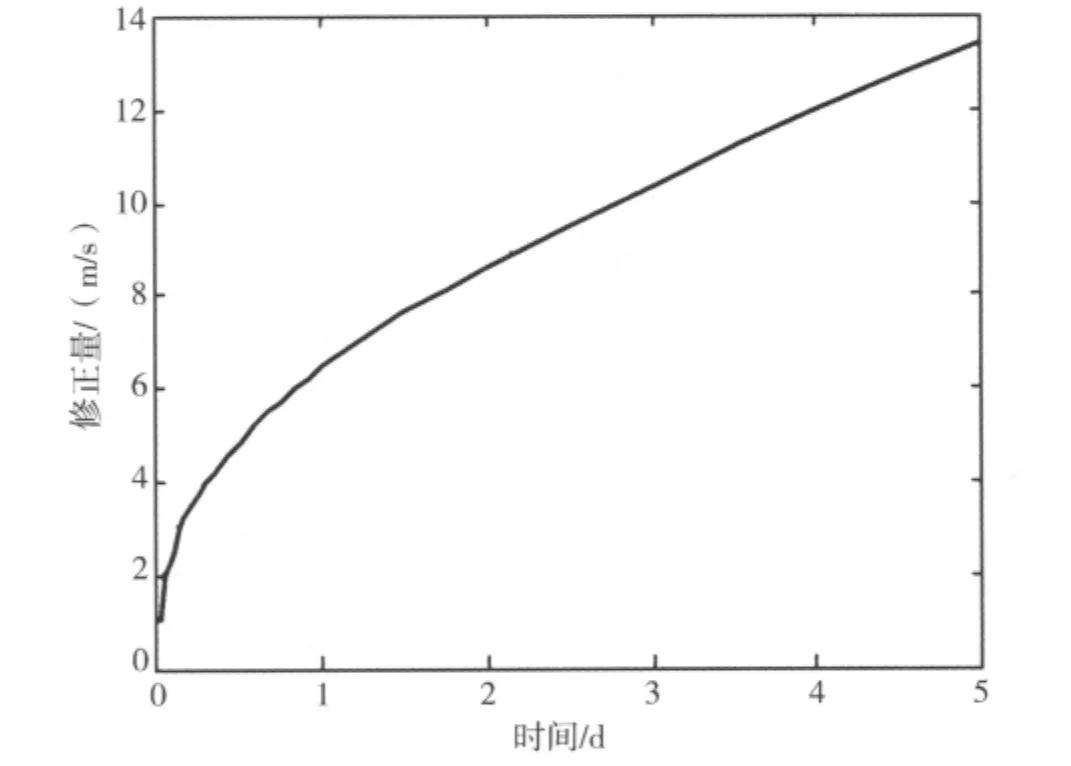
图5 修正量与修正时刻的关系Fig.5 Relation between correction maneuvers and correction time
不同初始发射速度误差在发射后1天末修正所需的修正量如图6所示.由图可见,修正量和误差量成正比.

图6 修正量与初始发射速度误差的关系Fig.6 Relation between correction maneuvers and initial launch velocity errors
2 误差源和摄动因素
在实际转移过程中,由于各种误差源和摄动因素的影响,探测器实际到达的转移轨道终点与期望的晕轨道入轨点往往存在偏差.本文考虑的误差源主要包括转移轨道初始发射误差、导航误差和中途修正引入的误差,摄动因素主要包括地球引力摄动、月球引力摄动和太阳光压摄动.
2.1 误差源
由于存在导航误差(E1)和转移轨道初始发射误差(E2),将会使得探测器的实际飞行轨道偏离标称轨道,因此必须进行中途修正,而中途修正又会引入修正速度误差(E3).
假定几个误差源均服从Gauss分布,均值都为零,方差各为(误差源方差取值与文献[4]相同,且增加了初始发射位置误差和时间误差):
E1:位置偏差为 10km(1σ),速度偏差为0.01m/s(1σ);
E2:位置偏差为 5.6km(3σ),时间偏差为 1s(3σ),速度大小偏差为0.36%(3σ),速度方向偏差为1.50°(3σ);
E3:速度大小偏差为3.00%(3σ),速度方向偏差为 2.06°(3σ).
2.2 摄动因素
在实际转移轨道修正过程中,除了上述3种误差源外,还应考虑地球非球形摄动、月球引力摄动以及太阳光压摄动等摄动因素.
(1)地球引力摄动
地球引力摄动中主要考虑J2项摄动的影响.仿真表明,J2项摄动对转移轨道影响较大.这主要是由于当卫星进入转移轨道后,需要在地球附近运行一段时间,J2项摄动将影响地球附近的转移轨道,由于转移轨道的敏感性,在晕轨道入轨点处将产生较大偏差.
(2)月球引力摄动
由于圆型限制性三体模型(CRTBP)将地球和月球看作位于地月公共质心的质点来处理,因此与实际模型有较大差异.仿真表明,月球引力摄动对转移轨道影响很大,将会大大增加修正量,并带来很大的末端误差.然而,若直接调整转移轨道入轨机动,使得受月球引力摄动影响的转移轨道能够到达晕轨道入轨点附近,则可大大降低中途修正代价.这样做尽管可以降低修正量,但末端误差仍然很大,对晕轨道的轨道保持造成负担.因此,适宜在标称转移轨道设计中考虑月球引力摄动.
(3)太阳光压摄动
仿真表明,太阳光压摄动对地球影响球内的转移轨道段影响非常小,而对晕轨道附近的转移轨道段影响较大,且卫星在晕轨道附近运行时间越长,所产生的位置误差越大.因此,太阳光压摄动对从地球停泊轨道到晕轨道近地点入轨的转移轨道影响很小,而对晕轨道远地点入轨的转移轨道影响较大,这主要是由于和近地点入轨相比,远地点入轨需要在晕轨道附近运行更长时间.
3 中途修正策略
本节主要采用分段式修正策略来进行转移轨道的中途修正研究,即当探测器到达预定的修正时刻,根据当前的测量值计算所需的修正量.
3.1 中途修正方案
确定中途最优修正次数和最佳修正时刻是中途制导策略问题.应用最广的是间距比(spacing ratio)策略[5],间距比策略的思想是尽快进行首次修正,以后每次修正时间间隔与前一时间间隔之比为常数,直至误差满足要求.在平动点转移轨道中途修正中,有文献根据转移轨道的几何特征来选取修正点[3-4],也有根据以往平动点任务的中途修正经验来确定修正序列[6].
由于飞向晕轨道的转移时间较长,必须进行多次中途修正机动(TCM).前期的研究表明,为了减少中途修正速度增量,宜尽早进行首次修正.但是,如果第一次修正时刻太早,残余误差被更多地放大,会加重以后的修正任务.另外,进入转移轨道后,地面对探测器的跟踪定轨还需要一段时间,因此第一次修正时刻不能太早.综合考虑,选择第一次修正时刻为发射后1天末.类似地,由于第一次修正机动主要用来修正初始发射误差,所需的修正量很大,将产生较大的中途修正执行误差,第二次修正时刻太早,残余误差会被更多地放大,因此,第二次修正时刻一般选择在发射后20天~30天末.其他修正时刻根据大量仿真得到.
为了研究修正时刻和修正次数对修正量和末端状态误差的影响,以晕轨道近地点入轨的转移轨道为例,制定如下2种修正方案,如图7和表1所示.

图7 晕轨道近地点入轨的转移轨道中途修正方案Fig.7 Trajectory correction maneuver schemes

表1 晕轨道近地点入轨的修正机动(TCM)方案Tab.1 Trajectory correction maneuver schemes
3.2 中途修正策略
设探测器的初始状态Ji和末端状态Ji+1之间的关系为

两状态之间的误差关系可线性化表示为

若初始状态Ji对应的末端状态Ji+1与标称末端状态存在一定偏差,则利用该式,通过迭代可计算出修正末端状态偏差所需的初始状态修正量δJi.初始状态取 Ji= [RiVi]T,由于修正时刻选定后,位置Ri是不可改变的,只能对速度Vi加以修正,则表达式(2)可进一步表示为

式中Ri+1和Vi+1为末端时刻的位置和速度.选择末端状态Ji+1=[H],H为实际末端状态Ji+1与标称末端状态之间的距离.

则由式(3)可得

式中δH=H*-H,由于期望的H*=0,因此有δH=-H.则修正量为

预先设定中途修正次数为N次,对应的修正时刻为ti,其中i=1,…,N,每一次修正均以下一次修正时刻卫星在标称轨道上的位置为目标,称为分段式修正策略,本文采用Matlab自带的ode45进行数值积分,仿真中末端位置误差小于10km.
4 Monte Carlo仿真及分析
Monte Carlo(蒙特-卡罗)方法,又称为随机抽样模拟方法或统计试验方法,其基本思想是通过对模型或过程的观察、抽样,利用统计信息给出解的近似值,而解的精度可用估计值的标准误差等形式表示.由于导致轨道产生偏差的因素很多,各种误差对轨道的影响程度不一,为了研究各种误差源和摄动因素对中途修正代价和入轨精度的综合影响,采用Monte Carlo方法仿真研究给出的中途修正方案和修正策略的效果.
4.1 未考虑摄动因素
采用3.1节给出的两种中途修正方案,利用分段式修正策略,按照2.1节给出的误差源进行1000次仿真,给出修正结果的统计分布如图8所示,置信水平如表2所示.

表2 未考虑摄动因素的置信水平(方案1方案2)Tab.2 Confidence levels of no perturbation factors(scheme 1scheme 2)
由上可见,合理增加修正次数将会大大减小末端位置误差和速度误差,修正消耗也相差不大.
4.2 考虑地球引力摄动
考虑地球引力摄动后,采用同样的修正方案、修正策略以及误差源,进行1000次仿真,置信水平如表3所示.

图8 转移轨道中途修正结果的统计分布(方案1方案2)Fig.8 Distribution of correction results(scheme1scheme2)

表3 考虑地球引力摄动的置信水平(方案1方案2)Tab.3 Confidence levels of considering earth gravitational perturbation(scheme 1scheme 2)
比较表3和表2可知,考虑地球引力摄动J2项后,修正量略有变化,对末端误差影响也较小.
4.3 考虑月球引力摄动
考虑月球引力摄动后,采用同样的修正方案、修正策略以及误差源,进行1000次仿真,置信水平如表4所示.

表4 考虑月球引力摄动的置信水平(方案1方案2)Tab.4 Confidence levels of considering moon gravitational perturbation(scheme 1scheme 2)
比较表4和表2可知,月球引力摄动对修正量影响很大,而且大幅度增加了末端位置误差和速度误差.
4.4 考虑太阳光压摄动
考虑太阳光压摄动后,采用同样的修正方案、修正策略以及误差源,进行1000次仿真,置信水平如表5所示.

表5 考虑太阳光压摄动的置信水平(方案1方案2)Tab.5 Confidence levels of considering sunlight pressure perturbation(scheme 1scheme 2)
比较表5和表2可知,太阳光压摄动对修正量影响不大,主要是增大了末端位置误差,末端速度误差也略有增加.
4.5 考虑地球摄动、月球摄动和太阳光压摄动
由上可知,修正方案2明显优于方案1,因此,在考虑地球引力摄动、月球引力摄动和太阳光压摄动后,采用修正方案2,进行1000次仿真,置信水平如表6所示.

表6 考虑3种摄动因素的置信水平(方案2)Tab.6 Confidence levels of considering three kinds of perturbation factors(scheme 2)
比较表6和表2可知,考虑3种摄动因素后,所需的修正量和末端误差都会增加,这主要是由月球引力摄动引起的.
5 结论
本文主要研究了误差源和摄动因素对修正量和修正效果的影响,以及转移轨道的中途修正问题.首先进行了初始发射误差的灵敏度分析,研究了存在初始发射位置误差和速度误差时,修正时刻与修正量之间的关系以及误差量与修正量之间的关系;然后分析了中途修正过程中需要考虑的转移轨道初始发射误差、导航误差和中途修正引入的执行误差等几种误差源以及地球引力摄动、月球引力摄动和太阳光压摄动等摄动因素;给出了分段式中途修正策略.以晕轨道近地点入轨的转移轨道为例,分析了几种误差源和摄动因素对转移轨道修正量和修正效果的影响,最后经Monte Carlo模拟给出了修正结果的统计信息.
[1] Serban R,Koon W S,Lo M W.Halo orbit mission correction maneuvers using optimal control[J].Automatica,2002,38(4):571-583
[2] Gómez G,Marcote M,Masdemont J J.Trajectory correction manoeuvres in the transfer to libration point orbits[J].Acta Astronautica,2005,56(7):652-669
[3] Jenkin A B,Campbell E T.Generic Halo orbit insertion and dispersion error analysis[C].AIAA/AAS Astrodynamics Specialist Conference and Exhibit,Monterey,California,August 5-8,2002
[4] Xu M,Xu S J.Trajectory and correction maneuver during the transfer from earth to Halo orbit[J].Chinese Journal of Aeronautics,2008,21(3):200-206
[5] 郗晓宁,曾国强,任萱,等.月球探测器轨道设计[M].北京:国防工业出版社,2001 Xi X N,Zeng G Q,Ren X,et al.Orbit design of lunar probe[M].Beijing:National Defence Industry Press,2001
[6] 李明涛,郑建华.平动点任务转移轨道中途修正研究[J].空间科学学报,2010,30(6):540-546 Li M T,Zheng J H.Research on transfer trajectory correction maneuvers for libration point missions[J].Chinese Journal of Space Science,2010,30(6):540-546
