灰色与线性回归组合模型在变形预测中的应用研究
2012-04-16郑伟涛丁啸
郑伟涛丁啸
(1.东华理工大学测绘工程学院,江西南昌330013;2.抚州市广播电视局,江西抚州344000)
1.引言
由于多种因素的影响,建构筑物在建设和使用的过程中,发生一定限差范围内的沉降均被视为正常现象,但如果超出限差范围,势必会对建构筑物的安全和稳定性造成影响。所以,对这些重要建筑物进行定期监测,并且根据监测数据对建筑物的沉降趋势做出准确的判断和预测,及时将沉降有关的信息和变形情况提供给项目相关人员以提高施工的效率和精度,从而为整个工程建设提供有力的技术支持和决策依据,是表达沉降监测成果的有效方法[1]。
回归分析法、时间序列方法、灰色模型法、人工神经网络法、遗传算法等都是预测建构筑物沉降的方法[2],这些方法都有大量的成果和实例。由于影响建构筑物沉降量的因素[3]多而杂,至今还没有一种预测方法能对其进行准确的预报。用不同的预测方法得出的结果可能会相差很大,这给实际应用中的模型选择和精度预测带来了很多不便。针对这些实际情况,我们引入了组合预测的思想,将灰色模型(GM(1,1))法、线性回归模型进行组合,与单一的灰色模型和简单的滑动平均做出对比,得出组合模型计算较准确,精度较高,并通过实例加以验证。
2.GM(1,1)模型原理
记原始序列为X0[4]:
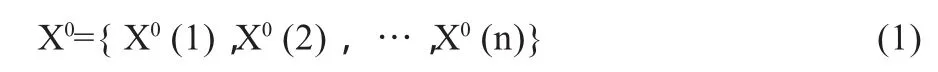
根据灰色系统理论对原始序列做1次累加生成后,得到生成序列X1(1),即:
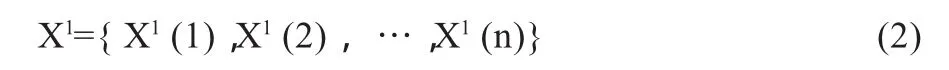
其中X1(t)可用下式进行计算:

系统预测模型GM(1,1)的白化形式的微分方程表示为:

对微分方程求解,得到其离散的通解为:
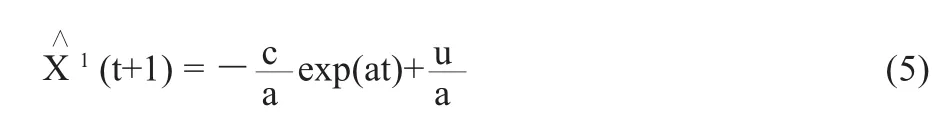
式中,c为积分常数,需要通过一个边界条件来确定。在目前所采用的预测模型中,都是假定:

式(4)在式(5)条件下的特解为:
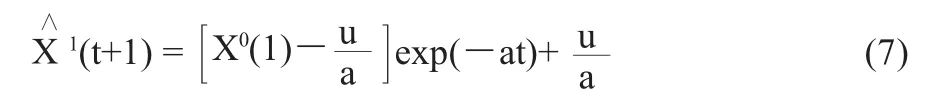

式中,B以及y用式(9)计算:
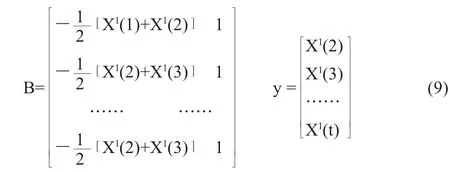
预测公式为:
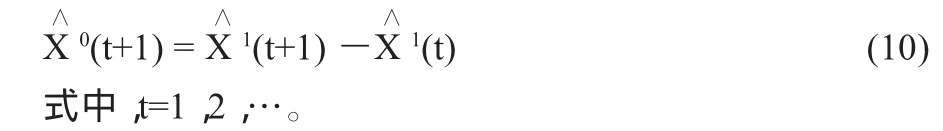
3.组合模型
由(4)可以将微分方程解为:
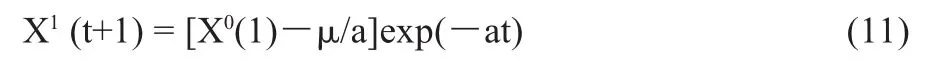
对X1(t+1)求导或做累减还原,得到原始系列的预测公式为:
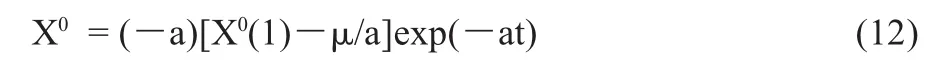
分析微分方程的解式(11),可以看出它的形式如下式:

用线性回归方程Y=aX+b及指数方程Y=a·exp(p)的和来拟合[5]累加生成X1(t),因此可将生成序列写成:
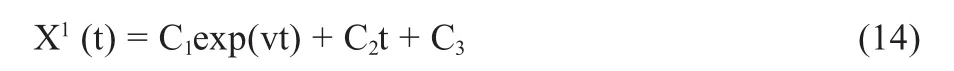
在上式中,参数v及C1,C2,C3需要确定。

并设:

同样有:
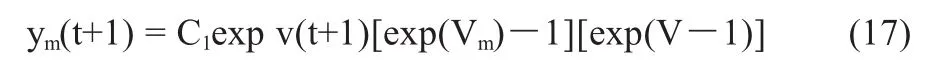
则上面两式相比为:

因此得到V的解为:



利用最小二乘法求得的C1,C2,C3估计值。
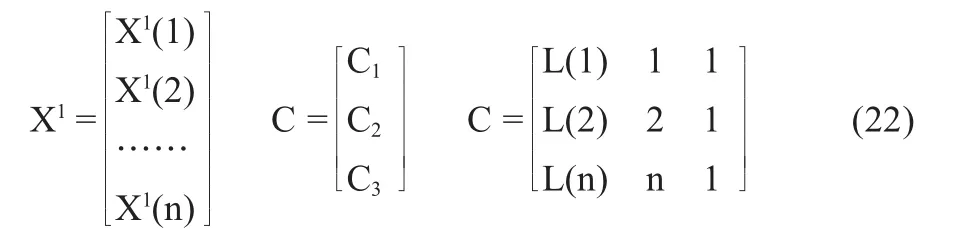
则有:X1=AC,从而:

得到生成序列的预测值为:

将上式的计算结果用一次累减[6]生成即可得到原序列X0的预测值。
4.模型的应用
江西省井冈山市某村滑坡隐患灾害防治工程主山体A号钻孔变形监测数据(孔底深度23.5M,时间2011年4月)如表1所示:
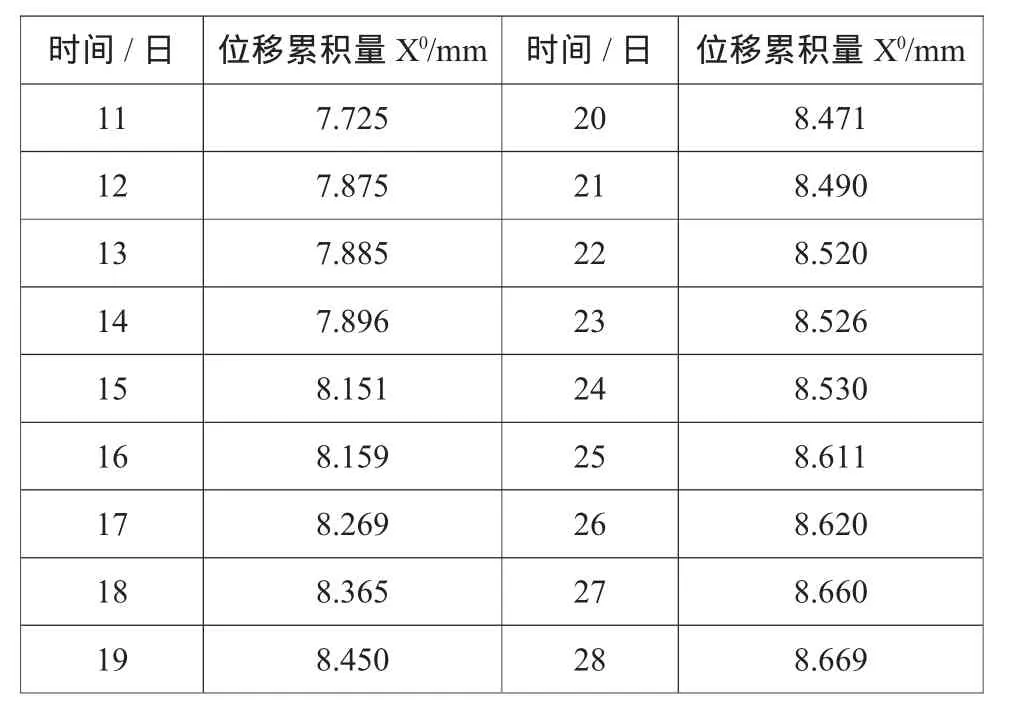
表1 主山体A号钻孔变形监测数据
用式(3),式(7),式(8),式(9)可以得到生成系列X1的时间相应函数为:
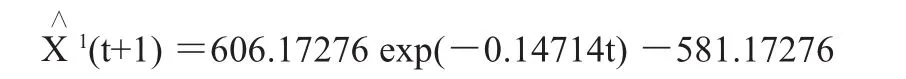
利用上式计算出各期模拟和预测值后,通过式(10)一次累减生成,求得各期的预测值、残差和相对误差如表2所示,预测值的平均相对误差为12.42%,预测29日沉降量的相对误差为12.39%,预测30日沉降量的相对误差为21.14%。
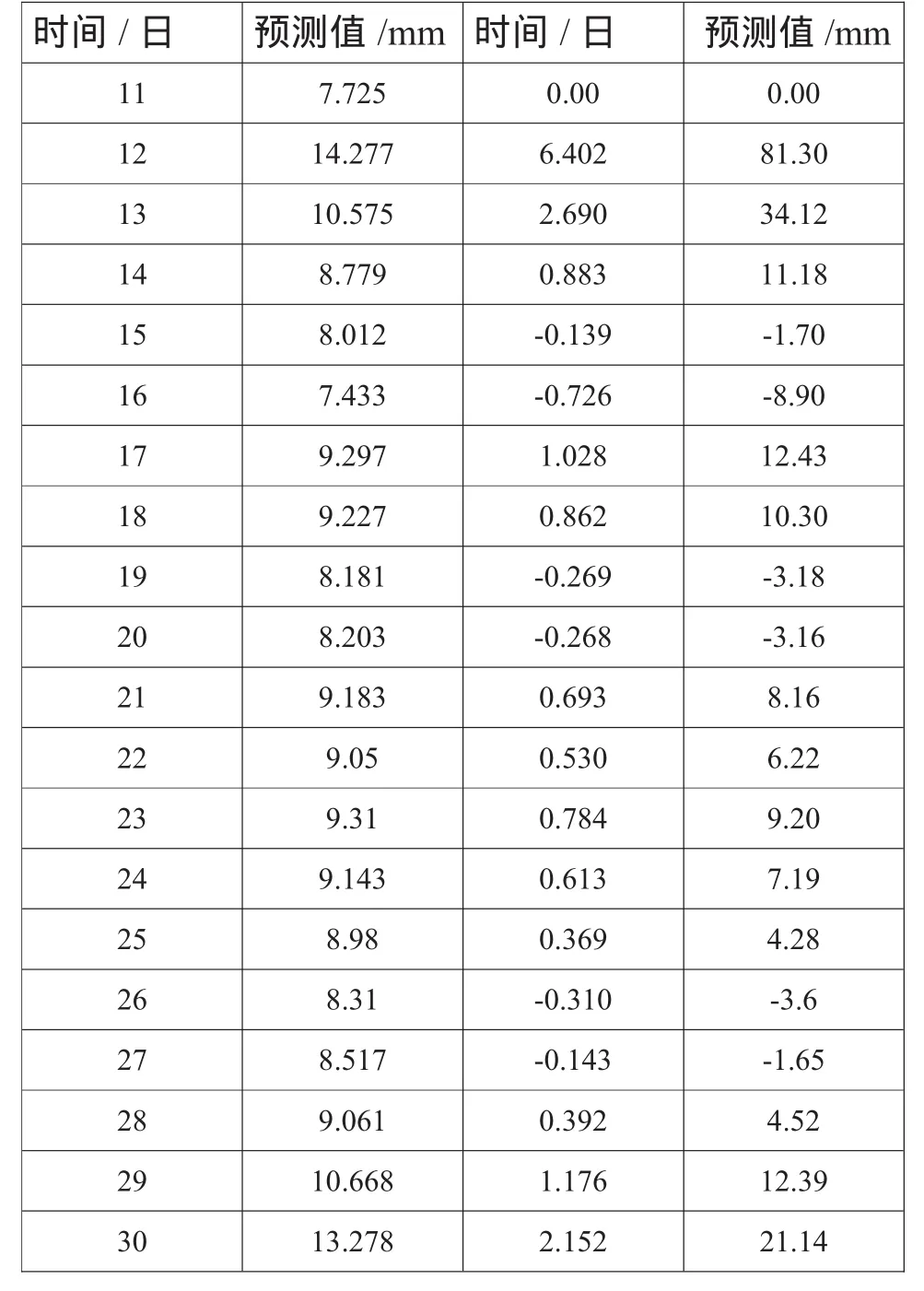
表2 各个时期的预测值、残差及相对误差
由灰色线性回归组合模型可得到其时间相应式为:

利用上式计算出各期模拟或预测值后,通过一次累减生成,求得各期的模拟值、残差和相对误差如表3示,预测值的平均相对误差为11.53%,预测29日沉降量的相对误差为2.39%,预测30日沉降量的相对误差为1.72%。
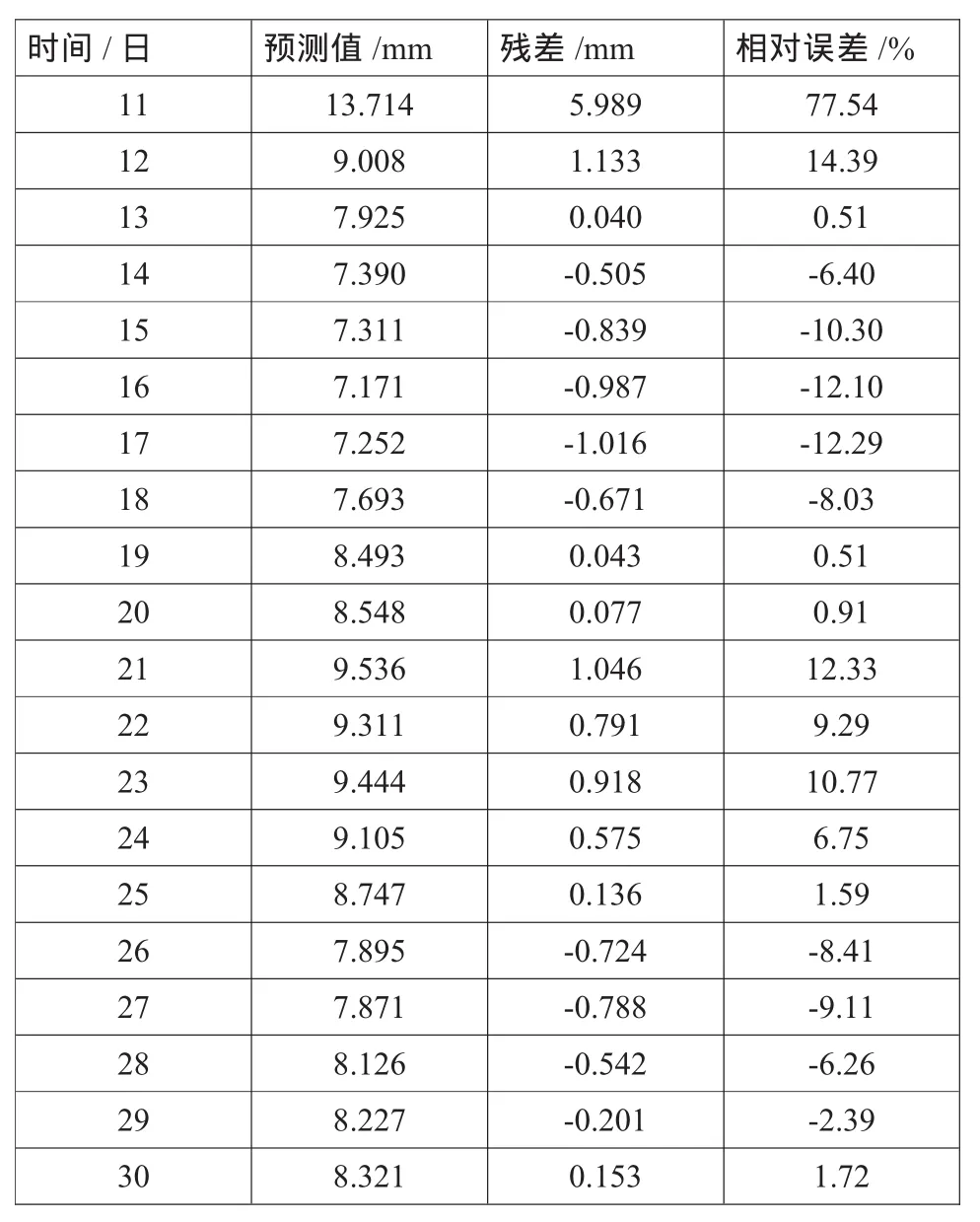
表3 各时刻预测值,残差值及相对误差
组合模型与单一的灰色模型的对比如表4所示:
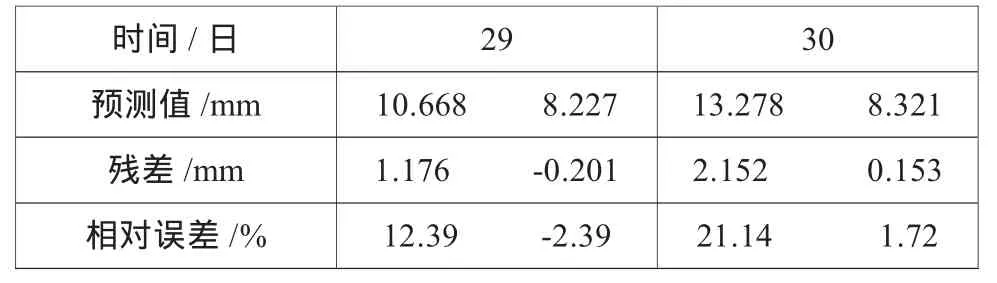
表4 29,30日预测值的对比
通过对比可知,组合模型的相对误差比单一灰色模型的误差要小得多,这说明了组合模型预测的比较准确,且精度要高于灰色模型。
5.结语
灰色系统理论[7]在数据量少的变形预测中的优势显而易见,很好的控制了数据的随机性、规律性和准确性。通过讨论GM(1,1)模型原理和GM(1,1)与回归组合模型原理的不同之处,并且用组合模型进行大样本实例计算,我们可知组合模型计算较准确,精度较高。利用灰色与回归组合模型能够解决单纯灰色模型不能解决的问题。
[1]邓聚龙.灰色控制系统[M].武汉:华中理工大学出版社,1986.
[2]何晓群,刘文卿.应用回归分析[M].北京:中国人民大学出版社,2001:59~60.
[3]傅立.灰色系统理论及其应用[M].北京:科学技术文献出版社,1992.
[4]黄声享,尹晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2003.
[5]刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社,2004.
[6]王穗辉,潘国荣.基于MATLAB多变量灰色模型及其在变形预测中的应用[J].土木工程学报,2005,38(05):24-27.
[7]导向科技MATLAB 6.0程序设计与实例应用[M].北京:中国铁道出版社,2001.
