基于遗传算法的改进神经网络在PI整定中的应用
2012-04-08黄振跃张新华
黄振跃,张新华
(江苏大学 电气信息工程学院,江苏 镇江 212013)
0 引言
随着智能控制技术的飞速发展,人工神经网络在工业控制领域得到了广泛的研究与应用[1-2]。神经网络不需要任何预定模型的知识,因此控制系统对噪声、参数变化及负载改变具有较强的鲁棒性。常规的神经网络通常利用模型参考自适应控制技术进行训练从而使电机达到跟踪控制的目的。但常规的神经网络存在容易陷入局部极小点、收敛速度慢、泛化能力差的问题[3],且网络只能在离线系统下进行参数识别。电机运行工程中参数动态变化时,以自适应控制方法为主的常规神经网络显示出局限性,使得对PI控制器参数的整定变得愈加困难。因此,能否跟随电机参数变化而进行在线的参数自整定对神经网络甚至整个电机控制系统来说具有重要的意义。
通常利用卡尔曼滤波算法进行神经元的计算。扩展卡尔曼滤波算法在前馈神经网络和递归神经网络的训练中已经显现出巨大的优势。由于卡尔曼滤波算法只保留上一时刻的协方差值,它运行速度快,通过不断的把协方差递归来估算最优值。跟梯度下降算法相比,扩展卡尔曼滤波的训练算法需要更少的训练数据,且在相同微分信息条件下更加简单可靠。由于扩展卡尔曼滤波不需要成批处理数据,因此对在线训练神经网络非常合适。但卡尔曼滤波器也有缺点,比如参数的变化可能会影响其性能,这限制了它的应用。
本文通过遗传算法来获得扩展卡尔曼滤波的最佳参数,进而求得神经元的权值并训练,从而实现PI参数的自整定。首先从PI自整定控制器的性能指标出发,阐述了递归神经网络结构、异步电机转速控制系统及扩展卡尔曼滤波的基本参数,说明了采用遗传算法求取卡尔曼滤波器最佳参数的可行性。最后借助MATLAB/simulink软件以异步电机为对象对提出的基于遗传算法的改进神经网络在PI整定中应用的有效性进行了建模与仿真。仿真结果表明,本文提出的方法能有效减小负载变化时的转速超调,系统具有良好的动静态性能。
1 PI自整定控制器及神经网络结构
1.1 PI自整定控制器性能指标
定义PI自整定控制器性能指标如下[4]:
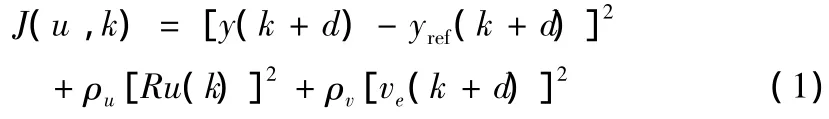
式中,u(k)、y(k)分别为输入、输出值。yref(k)为理想参考值。ρu、ρv为调整控制信号和系统响应精度之间平衡的权重系数。当J(u,k)对u(k)的微分结果为零时便可获得控制信号。
1.2 递归神经网络模型
神经网络由最基本的神经元组成。相对于单纯的静态网络,引入了网络反馈功能的动态递归神经网络的逼近能力具有更大的优越性。图1为递归神经网络模型的基本结构,图中Z-1为采样时间延时。uM(k)、YN(k+1)分别为神经网络的输入与输出,在离散时间k+1的前一步产生YN(k+1)。WN(N+M)为神经网络的权值。
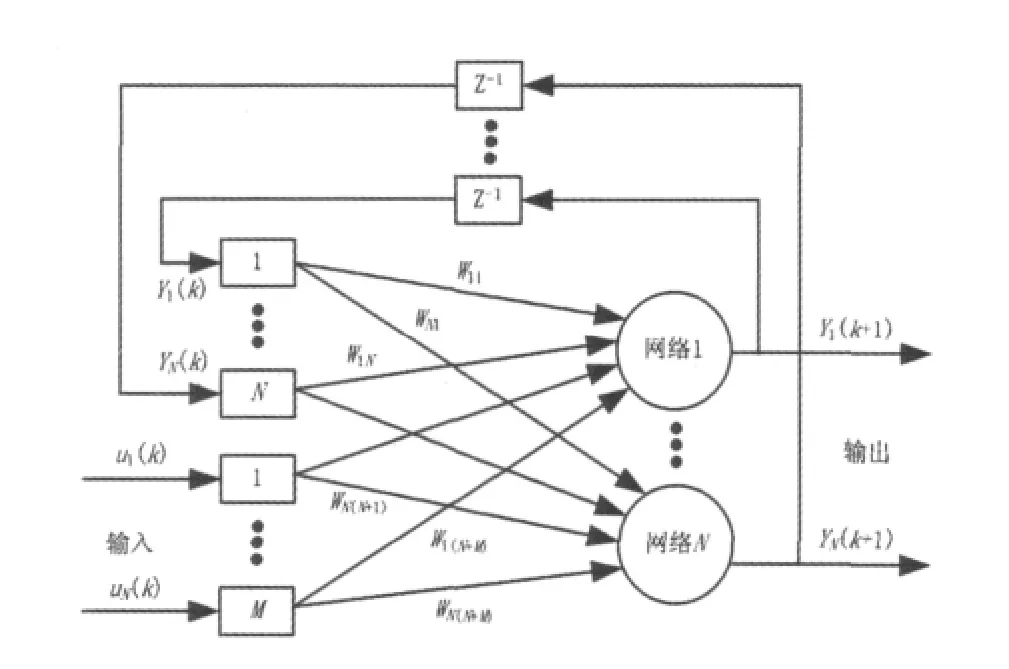
图1 递归神经网络模型的基本结构
根据神经网络的结构,可知异步电机模型参数如下:一个表示转矩电流分量 Iqs(k)的输入u1(k),一个表示转速输出值的Y2(k)。
1.3 异步电机转速控制系统
异步电机的速度输出模型是类似于式(2)的转速与输入的函数。

为了得到PI自整定控制器性能指标J(u,k)的最小值,采样时刻k时的控制输入u(k)如下:

式中,a0、a1、a2、b0、b1及 b2是由神经网络权值组构成的常量。
通过扩展卡尔曼滤波算法,可得到加权矩阵W。然后,再通过包含加权值的式(3)便可得到控制输入值u(k)。在异步电机中u(k)为转矩电流分量Iqs(k)。
1.4 扩展卡尔曼滤波
本文采用适合在线学习的扩展卡尔曼滤波算法来训练神经网络的权值[5]。卡尔曼滤波包含加权矩阵S(k),学习参数η(k)和协方差矩阵Q(k)等基本参数,这些参数对滤波性能具有重要的影响。通常利用试错法来确定参数。
2 基于遗传算法的卡尔曼滤波最佳参数
本文采用遗传算法来求取扩展卡尔曼滤波的初始最佳参数。遗传算法是全局最优算法,具有并行性和自动调整功能,在解决全局且复杂的优化问题上具有较为明显的优势,因此在寻找全局最优解的智能控制算法中已经得到了广泛的应用。它开始于包含一定染色体的初始种群,然后进行迭代运算,直至获得比父代更优秀的最优解。遗传算法由选择、交叉和突变等三种基本操作组成。
遗传算法的PI整定过程由如下步骤构成[6]:
步骤1:建立种群,在搜索空间中随机产生种群的个体;
步骤2:利用式(4)为种群中的每个个体估算ITAE;
步骤3:达到最大迭代次数G或者种群中某个个体的ITAE值小于预先设定值时停止;
步骤4:执行复制、交叉和突变操作。若某些个体超出其搜索空间,则保留相应的父代个体;
步骤5:返回步骤2,重新执行。
时间乘绝对误差的积分(ITAE)是衡量超调量和上升时间的重要指标,通过ITAE能寻找最优的比例和积分系数。本文采用ITAE来评价遗传算法的适应度函数,ITAE的定义如下[7]:
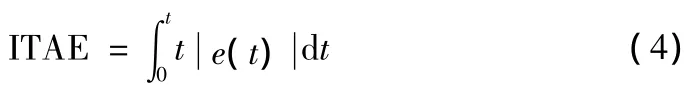
3 基于MATLAB/Simulink的建模与仿真
以异步电机为对象,借助MATLAB/Simulink软件建立仿真模型来验证本文提出的基于遗传算法的改进神经网络在PI参数整定中的有效性。遗传算法参数如下:每代种群有30个个体,最大迭代次数80,交叉概率0.76,突变概率0.003。个体位长为24位,分别包含8位归一化参数S(k)、8位归一化参数η(k)和8位归一化参数Q(k)。图2为控制系统框图。
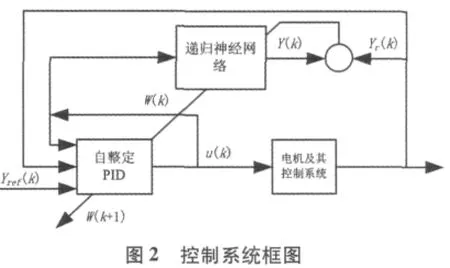
在递归神经网络 中,采用扩展卡尔曼滤波算法计算得到的神经元的权值进入自整定神经网络PI控制器以调节增益。在电机负载变化情况下考察转速响应波形。给定转速300 rad/s,仿真时间0.5 s。电机从空载启动运行,在 0.15 s时给定负载转矩3 Nm,PI控制器的采样时间为10 μs。由 基于遗传算法的改进神经网络得到的PI参数最优解Kp、Ki分别为9.417和768,如图3为ITAE曲线图。
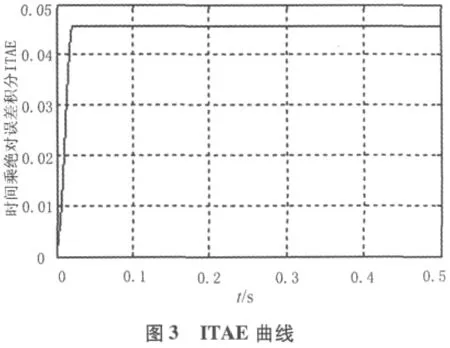
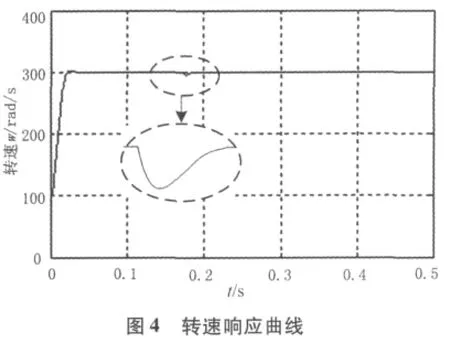
图4、图5分别为转速响应曲线和转矩响应曲线。从图4可以看出,在负载转矩从零到3 Nm突变过程中,转速超调量很小,因此相对于传统的神经网络控制器具有转速响应快速、恢复时间较短,在惯性变化时具有较高的鲁棒性。从图5可以看出,转矩响应很快并迅速达到新的稳态。
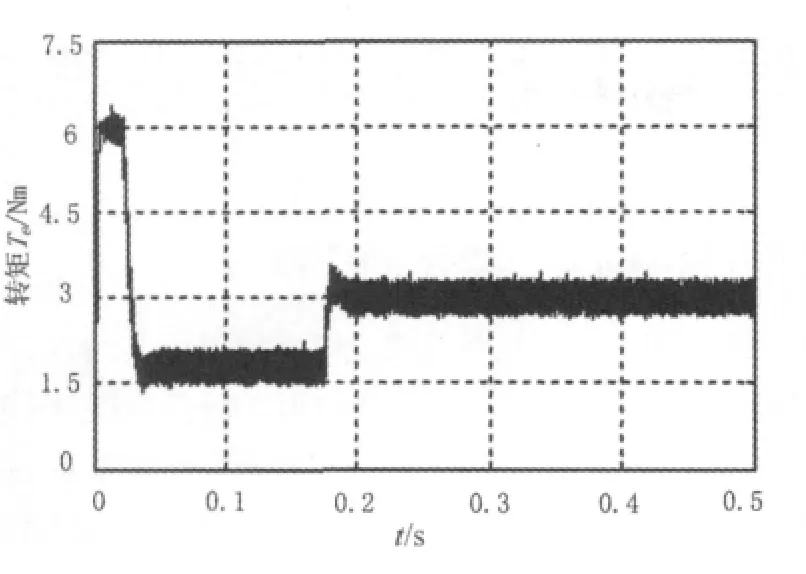
图5 转矩响应曲线
4 结束语
PI参数的在线自整定对电机控制系统来说具有重要的意义。针对常规神经网络不能在线进行参数识别的不足,本文提出了基于遗传算法的改进神经网络控制器。首先利用遗传算法进行卡尔曼滤波器的参数寻优,然后根据优化后的卡尔曼滤波器来计算神经元的权值,进而实现PI参数的自整定。本文提出的控制器采用递归神经网络模型来检测参数的变化,能够根据系统参数变化而自动调节增益,也能够弥补非线性控制系统的不确定性,控制器输出能直接用来进行参数的识别与调节。最后借助MATLAB/Simulink软件进行了建模与仿真,仿真结果验证了本文提出的改进神经网络的有效性。
[1] C FNascimento,A A Oliveria,A Goedtel,et al.Neural Network -Based Approach for Identification of the Harmonic Content of a Nonlinear Load in a Single - Phase System[J].IEEE Latin America Transactions,2010,8(1):65-73.
[2] SFerrari.Multi objective Algebraic Synthesis of Neural Control Systems by Implicit Model Following[J].IEEE Transactions on Neural Networks,2009,20(3):406 -419.
[3] 高骏,何俊佳.量子遗传神经网络在变压器油中溶解气体分析中的应用[J].中国电机工程学报,2010,33(30):121 -127.
[4] W.S.Oh,K.M.Cho,S.Kim,et al.Optimized Neural Network Speed Control of Induction Motor using Genetic Algorithm[C].International Symposium on Power Electronics,Taormina,Italy,2006:1377-1380.
[5] G..V.Puskorius,L.A.Feldkamp.Neurocontrol of Nonlinear Dynamic Systems with Kalman Filter Trained Recurrent Networks[J].IEEE Transactions on Neural Networks,1994,5(2):279-297.
[6] B.Naresh,M.V.Kumar,N.Y.Smieee.GA Based Tuning of PI Controller[C].IEEE Recent Advances in Intelligent Computational Systems,Trivandrum,India,2011:321-325.
[7] 李亮亮,何勇,叶海翔.基于ITAE最优控制的永磁同步电机矢量控制仿真[J]. 电机与控制应用,2011,38(6):31-33.
