p-光滑性的简单原子刻划

刘志民

(河北工程大学理学院，河北邯郸056038)

0 前言

原子分解作为一种有效工具在鞅论研究中起着重要的作用［1－4］。文献［5］就是运用这种技巧给出了Hp鞅论很多重要不等式的简单证明。文献［6］研究了B值鞅空间的原子分解，利用原子分解讨论了取值空间的几何性质及鞅空间的相互嵌入关系。

设(Ω，Σ，P)为完备概率空间，(Σn)n≥0为Σ 的一列递增子σ-代数，满足Σ=σ(∪n≥0Σn)。分别记期望和关于Σn的条件期望为E和En。设(X，)为Banach空间，f=(fn)n≥0为X值鞅，其鞅差为d fn=fn－fn－1(n≥1)，分别记其极大函数和条件均方函数为 f*=supn和 σ(p)(f)=。本文将考虑B值鞅空间pΣq，即

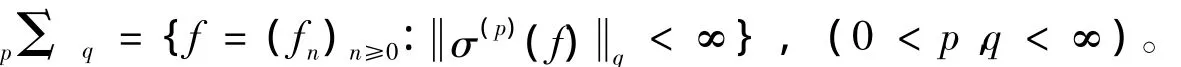
本文建立了Banach空间值鞅空间pΣq的简单原子分解定理，利用鞅的简单原子分解给出了取值空间p-光滑性的一种刻划。

定义［7］设0＜α，r≤∞，1≤p＜∞。一个B值可测函数a称为一个(1，α，r;p)简单原子，若存在n∈N，H∈Σn，使得:

(Ⅰ)an=Ena=0。

(Ⅱ){a≠0}⊂H。

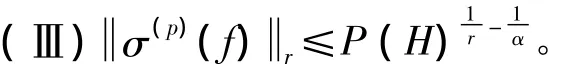
将(1，α，r;p)简单原子的全体简记为pSA1(α，r)。

引理［8］设X为Banach空间，1＜p≤2，1＜α＜∞，则以下几条等价: (Ⅰ)X同构于p一致光滑空间。

在本文中，常用C表示一个常数，允许在不同的地方取不同值。用Z表示整数集。

1 主要结果和证明

定理 设Χ为Banach空间，1＜p≤2。

(Ⅰ)若Χ同构于p一致光滑空间，0＜q≤p，则对任意X值鞅f=(fn)n≥0∈pΣq存在一列{g(k)}∈pSA1(q，∞)(k∈Ζ)和一列非负实数μ=(μk，k∈Ζ)∈lq，使得

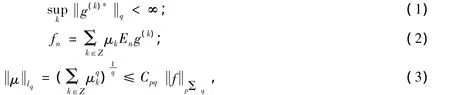
其中，Cpq为依赖于p和q的正常数;而且，级数μkg(k)依pΣq范数收敛于f。

(Ⅱ)设0＜q≤1，Χ同构于p一致光滑空间。若对X值鞅f=(fn)n≥0，存在一列g(k)∈pSA1(q，∞)(k∈Ζ)和一列非负实数μ=(μk，k∈Ζ)∈lq，使得式(2)成立，则f∈pΣq且

其中，″inf″遍历所有f形如式(2)的分解。

(Ⅲ)若0＜q≤1且对任意X值鞅f=(fn)n≥0∈pΣq，存在一列g(k)∈pSA1(q，∞)(k∈Ζ)和一列非负实数μ=(μk，k∈Ζ)∈lq使得式(1)和式(2)成立，则Χ同构于p一致光滑空间。

证明 (Ⅰ)设f=(fn)n≥0∈pΣq，对任意k∈Ζ定义如下

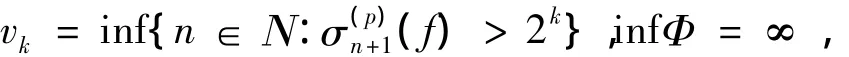
显然，{vk}k∈Ζ非降且当k→∞时，vk→∞。

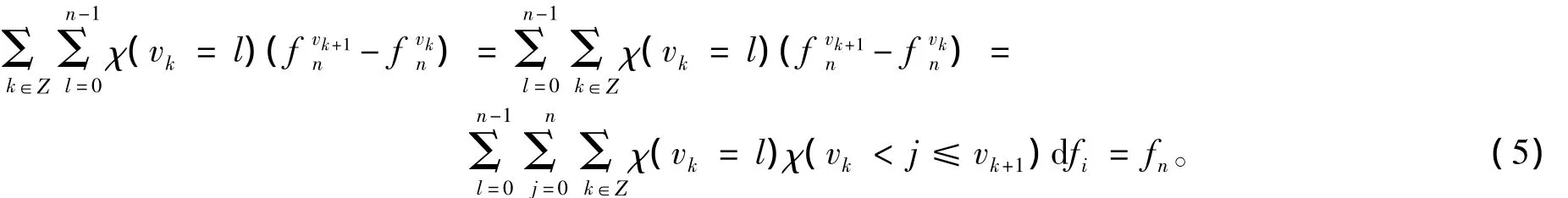
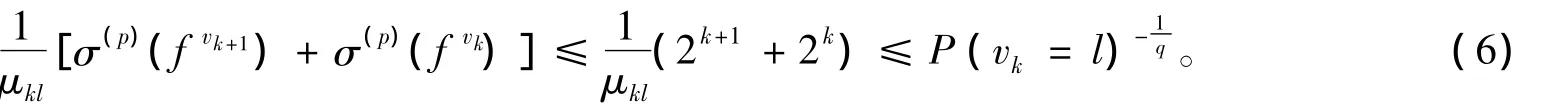
当X同构于p一致光滑空间时，由引理和式(6)知

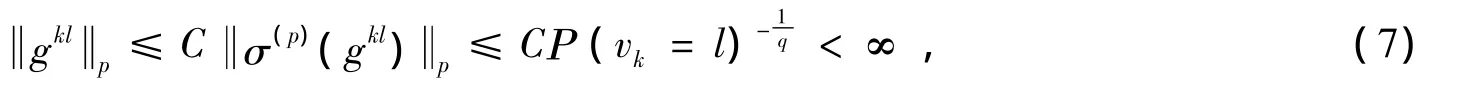
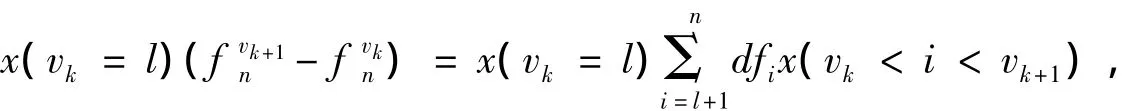
据上式El(gkl)=0。对kl∈Ζ重新排列，则得一可数列，以下总是假设k对应于kl。由式(5)知式(2)成立。且

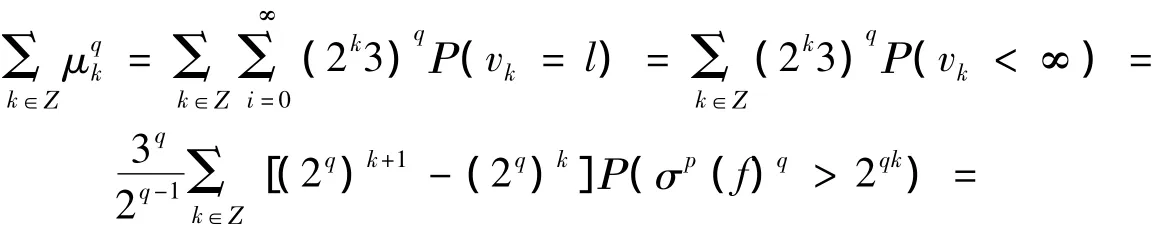
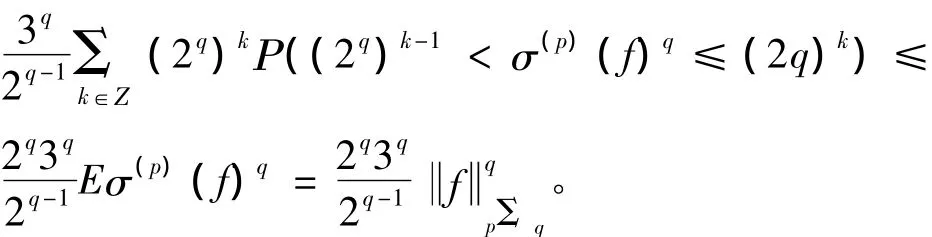
由引理知， E(g(k)*)q=E(g(kl)*)q=E(g(kl)*x(vk=l))q≤

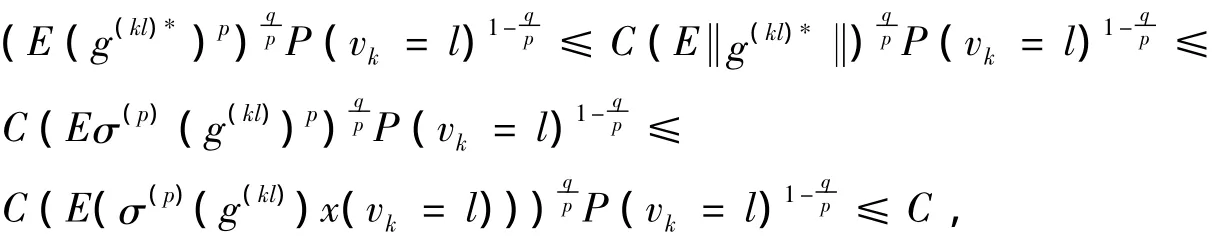
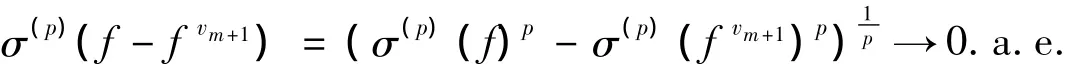
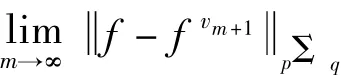
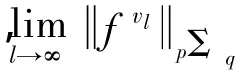
(Ⅱ)假设0＜q≤1且f=(fn)有形如式(2)的分解，容易验证下列式子成立

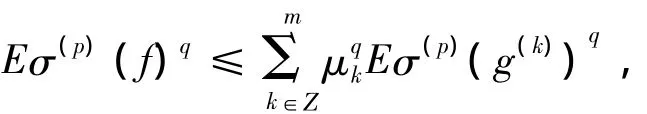
由p(1，q，∞)简单原子的定义知，在集{vk≠l}上σ(p)(q(kl))=0。所以

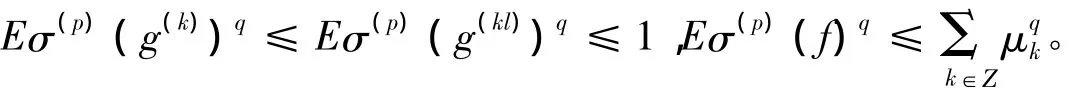
故f∈Σpq且式(4)成立。

(Ⅲ)设f=(fn)n≥0为X值鞅，满足E＜∞，由于

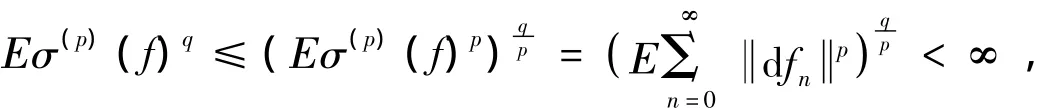
故f∈pΣq，由已知条件知存在形如式(2)的分解。注意到

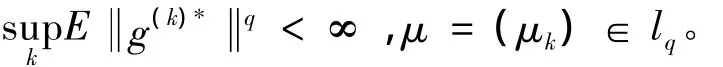
因gk是相应的简单原子，故g(k)n→g(k)，n→∞，k∈Ζ。由上式知(fn)依概率收敛。从而，根据引理知X同构于p一致光滑空间。

［1］ Liu Peide，Yu Lin.B-valued Martingales Spaces with Small Index and Atmotic Decomposition［J］.Science in China:A，2001，44(11):1361－1372.

［2］ Weisz F.Martingale Operators and Hardy Spaces Gene Rated by Them［J］.S tudia Math，1995，114:39－70.

［3］ Long R L.Martingale Spaces and Inequa Lities［M］.Beijing:Peking University Press，1993.

［4］ 任颜波.一类部分和序列的范数收敛性［J］.河南科技大学学报:自然科学版，2007，28(4):84－86.

［5］ Weisz F.Martingale Hardy Spaces and Their Applications in Fourier Analysis［M］.LNM:Springer-Verlag，1994.

［6］ Liu Peide，Hou Youliang.Atomic Decompositions of Banach-space-valued Martingales［J］.Science in China:A，1999，42 (1):38－47.

［7］ 任颜波，侯友良.Banach空间值鞅上的拟局部算子［J］.数学杂志，2007，27(6):725－730.

［8］ 刘培德.鞅与Banach空间几何学［M］.武汉:武汉大学出版社，1993.