功能梯度圆柱壳自由振动的影响因素分析
2012-04-07梁斌,项爽
梁 斌,项 爽
(河南科技大学规划与建筑工程学院,河南洛阳471003)
0 前言
功能梯度(FG)圆柱壳作为一种由新兴材料制成的结构构件,凭借其耐高温和良好的几何特性等优点,逐步在航空、航天、船舶等领域得到广泛应用,继而推动了很多对各种圆柱壳的固有频率及自由振动特性的研究。文献[1]用Love的一阶理论来计算旋转FG圆柱壳的固有频率,研究了幂指数、x和θ方向的波数、厚度-半径比对简支旋转FG圆柱壳固有频率的影响;文献[2]用有限元分析软件ANSYS对增强型夹层圆柱壳的自由振动进行了分析;文献[3]研究了边界条件对旋转去顶锥形多层圆柱壳的自由振动的影响;文献[4]利用Love一阶理论,以梁函数为轴向模态关系,研究了边界条件对多层圆柱壳的固有频率的影响;文献[5]采用Runge-Kutta法和多尺度法对轴向运动分层复合材料薄壁圆柱壳的非线性振动特性进行了研究;文献[6]基于经典Love薄壳理论,采用Rayleigh-Ritz法分析了两端简支边界条件下FG圆柱壳的自振特性,并探讨了体积分数和材料组分对固有频率的影响;文献[7]研究了指数型体积分数对FG圆柱薄壳振动频率的影响;文献[8]对弹性边界条件下圆柱壳的自由振动进行了分析;文献[9]研究了不同边界条件对FG圆柱壳固有频率的影响;文献[10]采用DQM方法分析了多种边界条件下圆柱壳的自由振动。由于功能梯度材料参数与空间坐标相关联、其控制方程是变系数的,直接获得解析解在数学上有诸多困难,相关研究文献十分有限[11]。
本文采用Love一阶壳体理论,建立应变-位移、曲率-位移关系,用Rayleigh-Ritz法得出FG圆柱壳自由振动固有频率的特征方程,研究了S-S、F-S及C-C这3种不同边界条件下壳体的固有频率,从体积分数、材料组分和边界条件等因素探讨对自由振动的影响。
1 FG圆柱壳自由振动的理论推导
功能梯度(FG)圆柱壳的平均半径为R,长度为L,厚度为h,几何外形如图1所示。
用Rayleigh-Ritz法求FG圆柱壳的固有频率,根据能量最小原理,得到Lagrange函数形式

FG圆柱壳的应变能表示为

图1 FG圆柱壳模型
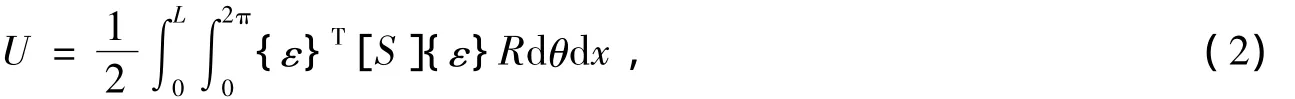
式中,

Aij、Bij和Dij(i,j=1,2,6)分别为壳体的拉伸刚度、耦合刚度和弯曲刚度;Qij(i,j=1,2,6)为折算刚度,
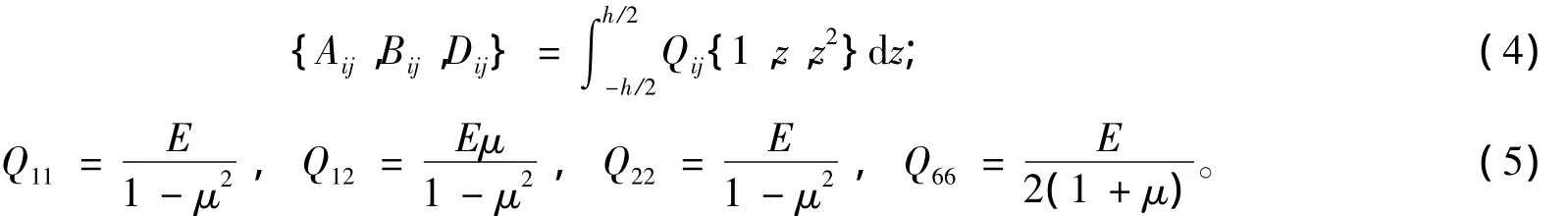
用Love一阶壳体理论分别描述曲面应变(e1,e2,γ)及曲面曲率(k1,k2,τ)与位移的关系如下
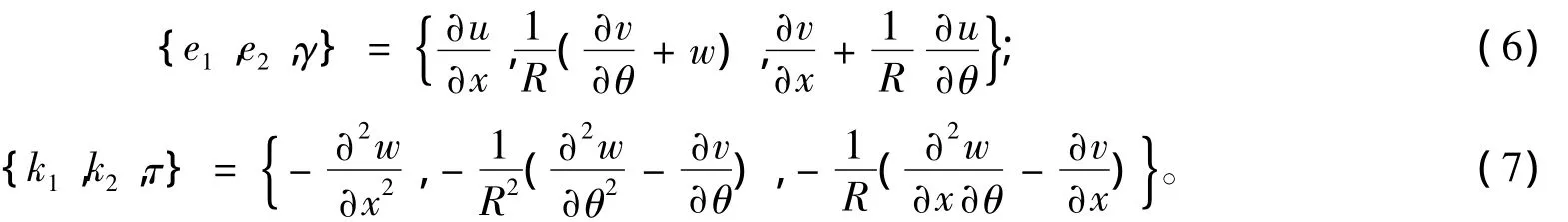
不计转动惯量,FG圆柱壳的动能表示为

式中,u、v、w分别表示x、θ、z方向的轴向、环向和径向位移分量,

式中,N为幂率指数,其取值范围为0≤N≤∞;弹性模量E、Poisson比μ和质量密度ρ分别取决于构成FG圆柱壳的不同材料组分。
假设位移函数u,v,w的形态形式对于空间变量x、θ及时间变量t来说是分离的,

式中,A、B、C为振动振幅;n为周向波数;ω为固有角频率。
取Lagrange函数关于振幅A、B、C的极值,得到3个联立方程

导出振动特征方程,用于求解固有频率和模态


式中,αi(i=0,1,2,3)是常系数。由式(14)可得到3个固有频率,取其中最小者为研究对象。
2 轴向形态关系及边界条件
可以表达轴向形态关系的代数函数有很多,如梁函数、Fourier级数形式的三角函数、多项式函数等,它们都满足壳两端的边界条件,本文采用的轴向形态关系为
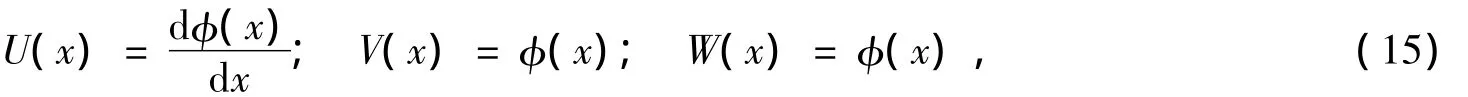
式中,特征梁函数φ(x)[12]定义为
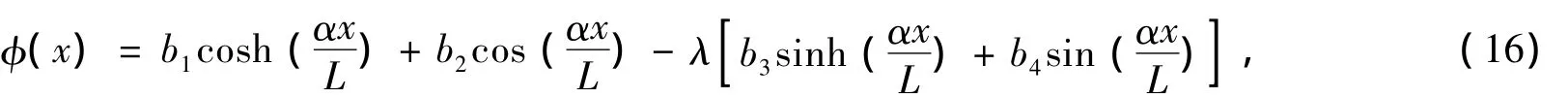
式中,bi(i=1,2,3,4)和λ与边界条件有关。
圆柱壳的边界条件可以表示为

3 算例与分析
将本文结果与已有文献成果做对比,表1验证了本文结果的有效性和正确性。计算频率参数时,壳体的各项参数指标为:h/R=0.01,L/R=20,E=2.050 98×1011N/m2,μ=0.3,ρ=8 900 kg/m3,p=1,m=1。
表2给出了文中所用FG圆柱壳的组分材料参数(T=300 K)。
表1 各项同性圆柱壳两端简支时的频率参数Ω=ωR ((1-μ2)ρ)/E对比分析
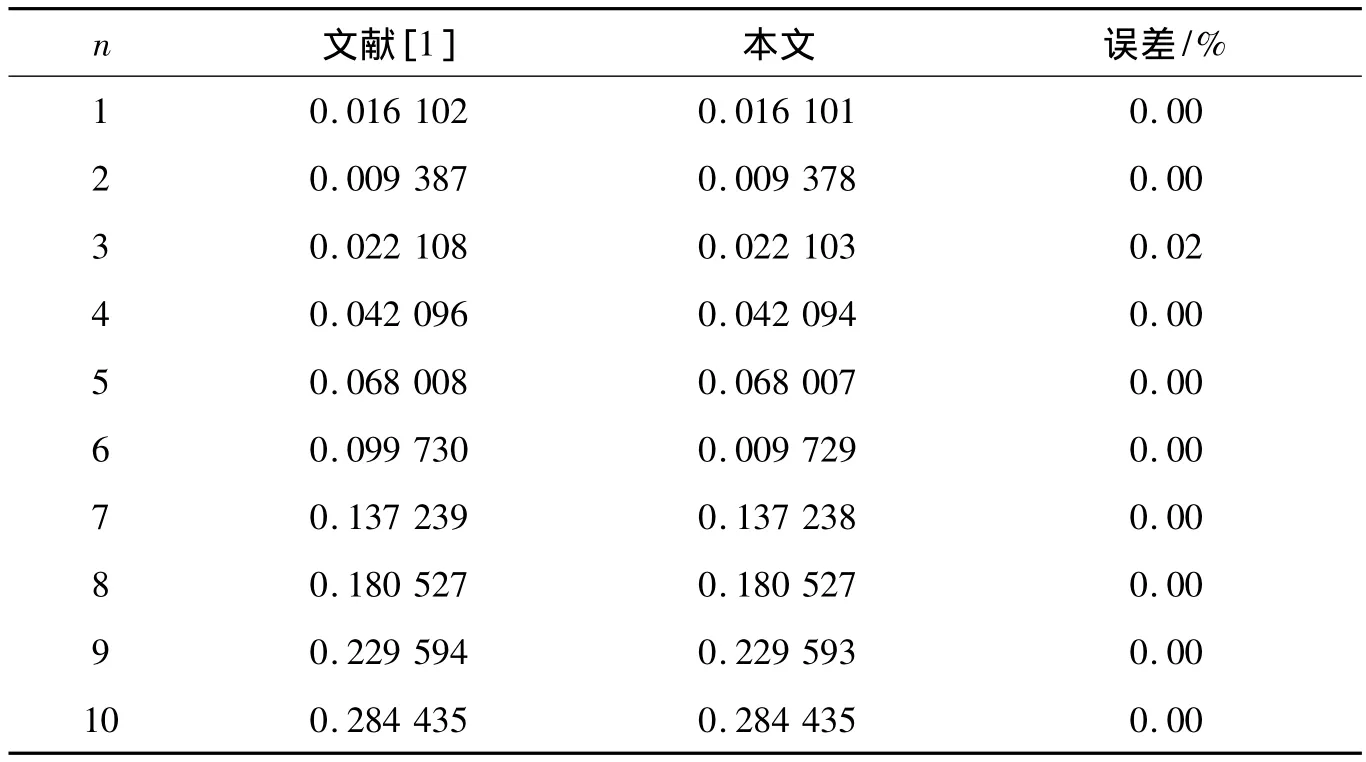
表1 各项同性圆柱壳两端简支时的频率参数Ω=ωR ((1-μ2)ρ)/E对比分析
n文献[1] 本文 误差/% 1 0.016 102 0.016 101 0.00 2 0.009 387 0.009 378 0.00 3 0.022 108 0.022 103 0.02 4 0.042 096 0.042 094 0.00 5 0.068 008 0.068 007 0.00 6 0.099 730 0.009 729 0.00 7 0.137 239 0.137 238 0.00 8 0.180 527 0.180 527 0.00 9 0.229 594 0.229 593 0.00 10 0.284 435 0.284 435 0.00

表2 材料参数表
表3给出了材料组分为不锈钢和氧化锆时的壳体在F-S边界条件下,通过改变体积分数对FG圆柱壳固有频率的影响。由表3可以看出:随着体积分数的不断增大,FG圆柱壳的固有频率也逐渐增大;但体积分数从0.5变化到30,对壳体的固有频率影响不显著。

表3 不同体积分数下FG圆柱壳的固有频率(m=1,h/R=0.002,L/R=20)
表4给出了F-S边界条件下,6组材料分别复合时,材料组分对固有频率的影响。由表4可以看出:在相同边界条件下,材料组分对壳体的固有频率影响较大;且周向波数n越大,影响越显著;其中铝/氧化锆组合的固有频率最大,钛合金/镍组合的固有频率最小。
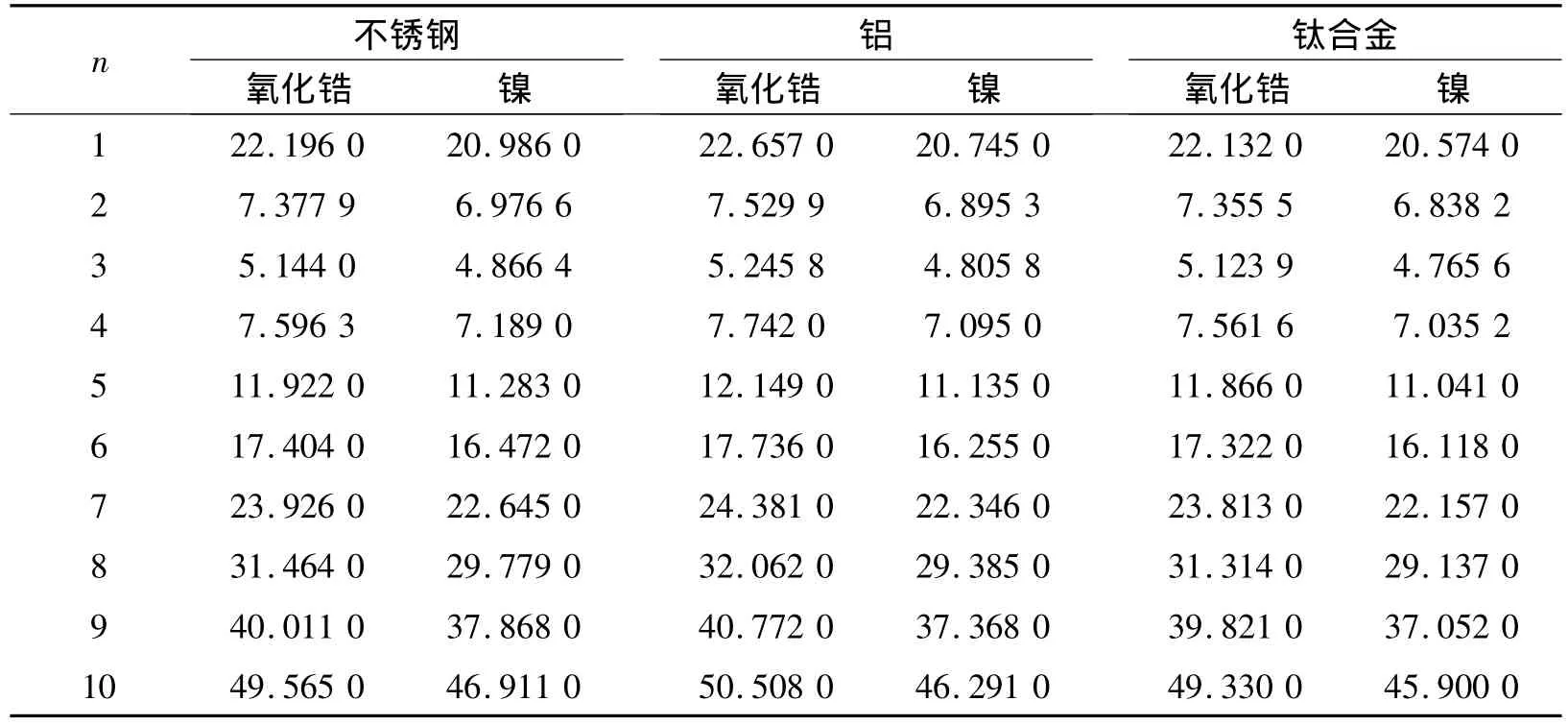
表4 不同材料组分时FG圆柱壳的固有频率(m=1,N=1,h/R=0.002,L/R=20)
表5给出了S-S、F-S及C-C这3种不同边界条件对固有频率的影响,由表5可以看出:边界条件对固有频率的影响很大,特别是在周向波数n≤3的情况下;又以C-C边界条件下的的固有频率最大,S-S边界条件下的的固有频率最小;它们有着相似的变化规律。

表5 不同边界条件下FG圆柱壳的固有频率(m=1,N=1,h/R=0.002,L/R=20)
4 结论
本文通过研究不同因素对FG圆柱壳固有频率的影响,得出如下结论:(1)体积分数、材料组分和边界条件都对固有频率有影响;(2)固有频率随体积分数的增大呈增大趋势,但变化不显著;(3)材料组分对固有频率的影响较大,且周向波数n越大,影响越显著;(4)边界条件对固有频率的影响很大,且主要表现在周向波数n≤3的情况下;(5)不同边界条件下的固有频率有着相似的变化规律,又以C-C边界条件下的固有频率最大,S-S边界条件下的固有频率最小。
[1] 项松,李广超,张魏,等.旋转功能梯度圆柱壳的固有频率计算[J].应用数学和力学,2012,33(3):332-341.
[2] 朱波,周叮,刘庆伟.芯材增强对夹层圆柱壳动力学性能影响的有限元分析[J].振动与冲击,2012,31(6):42-47.
[3] Li H.Influence of Boundary Conditions on the Free Vibrations of Rotating Truncated Circular Multi-layered Conical Shells[J].Composites:Part B,2000,31:265-275.
[4] Lam K Y,Loy C T.Effects of Boundary Conditions on Frequencies of a Multi-layered Cylindrical Shell[J].Journal of Sound and Vibration,1995,188(3):363-384.
[5] 李健,郭星辉,杨坤,等.轴向运动复合材料圆柱壳的非线性振动研究[J].固体力学学报,2011,32(2):176-185.
[6] Loy C T,Lam K Y,Reddy JN.Vibration of Functionally Graded Cylindrical Shells[J].International Journal ofMechanical Sciences,1999,41(3):309-324.
[7] 沙哈A G,曼穆德T,那姆M N.指数型体积分数功能梯度材料的薄壁圆柱壳振动[J].应用数学和力学,2009,30 (5):567-574.
[8] Zhou H J,LiW Y,Lv B L,etal.Free Vibration of Cylindrical Shellswith Elastic-support Boundary Conditions[J].Applied Acoustics,2012(73):751-756.
[9] Pradhan SC,Loy C T,Lam K Y,et al.Vibration Characteristics of Functionally Graded Cylindrical Shells Under Various Boundary Conditions[J].Applied Acoust,2000,61(1):111-129.
[10] Zhang L,Xiang Y,Wei GW.Local Adaptive DifferentialQuadrature for Free Vibration Analysis of Cylindrical Shellswith Various Boundary Conditions[J].International Journal of Mechanical Sciences,2006,48:1126-1138.
[11] 梁斌,杨民献,陈殿云,等.弹性圆柱壳的振动优化设计[J].洛阳工学院学报,2002,23(3):94-97.
[12] Loy C T,Lam K Y.Vibration of Cylindrical Shells with Ring Support[J].International Journal of Mechanical Sciences,1997,39(4):455-471.
