油气输送管线可靠度反问题分析
2012-04-01黄更平陈金梅金誉辉
黄更平,陈金梅,金誉辉
(1.广西特种设备监督检验院,广西 南宁 530219;2.广西工业职业技术学院,广西 南宁 530003)
压力管道主要用来输送原油、成品油、天然气、水、煤气等各种物料的,在使用中由于物料本身的特性、材料各种缺陷的存在、材料老化等原因,可能引起燃爆和重大灾难性较大的事故[1]。因此,压力管道的可靠性问题是管道运输业的首要问题。
常规压力管道可靠性设计计算中,通常采用正分析法,即在给定设计参数统计特性条件下,对管道进行可靠性分析。但是,有些问题是在给定结构的目标可靠度指标的基础上,反算出结构所需的材料参数和集合参数。可靠度反分析问题包括均值和标准差的确定、已知变异系数求均值、已知均值、标准差求变异系数等问题。目前,国内已将可靠度反分析方法应用于桥梁和岩土工程等方面的研究[2~3],但在管道参数的设计计算方面很少报道。本文主要利用可靠度反分析法研究压力管道的设计参数问题,推导了设计变量的迭代公式,并用正分析法—改进的一次二阶矩法验证该方法的有效性和准确性。
1 基本理论
1.1 改进的一次二阶矩法[4~5]
设结构的极限状态方程的表达式为:

式中 X=(x1,x2,……xn)为 n 个服从正态分布且相互独立的随机变量。
利用可靠性理论的改进一次二阶矩法(即验算点法)进行求解。步骤如下:
(1)选择初值:根据极限状态方程的各参数的均值赋予初值;

其中,μX为 X 的均值且有 μX=(μx1,μx2,……,μ xm);
(2)计算方向余弦:
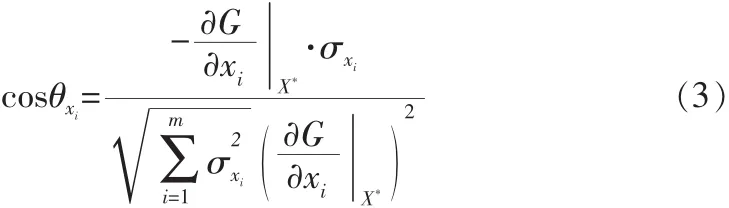
(3)X*和可靠性指数β的关系式为:

(4)将(3)中两个公式带入式(1)求出 β;
(5)把求得的β值带入(3)中两个公式,得到X*;
(6)以求得新X*重复第二步到第四步,直到所求得β与上一次计算的β小于要求的误差,则程序结束。并以最后一次的作为可靠性指数。
(7)求零件的失效概率F为:

改进的一次二阶钜法只适用于正态变量。工程实际中很多随机变量并不完全服从正太分布,因而当各随机变量为非正态分布时,利用映射变换法将任意分布的随机变量 X=(x1,x2,……xn)转换成正态分布变量,即非正态随机变量的当量化过程:

这里函数F(*)是关于变量xi的累计密度分布函数,Φ(*)是标准正态分布函数。
2.2 可靠度反分析方法
所谓的可靠度反问题,就是已知结构的极限状态,需要确定设计参数,以达到在一定保证率下,结构的抗力不低于载荷效应。因而问题可以看作是在指定可靠度指标的前提下,求解极限状态方程中影响结构的某些设计参数。
设极限状态方程G(X)处于变量无关的标准正太空间里,随机变量 u=(ux,uθ)是由满足特定分布的基本随机变量和待求的设计变量uθ组成,而ux和uθ分别为x和θ经过当量正态化以后的标准正态分布变量,在通常的情况下把θ的均值或标准差作为待求的设计变量。对于给定的目标可靠度指标βi,则可靠度的反问题计算步骤可以表述为[6~7]:
已知:目标可靠度指标βi;待求的设计变量θ(θ的均值或标准差);约束条件:min u =
首先将满足某种分布的随机变量xi,θ按照公式(6)、(7)进行当量正态化,将其变为标准正态空间下的随机变量。可靠度反问题求解正态分布的设计参数计算步骤如下:
(1)假设极限状态方程 G(X)=g(x,θ),其中 θ为设计参数值,给定的可靠度指标为,并假设u(k)=(u1(k),u2(k),……,un(k))和 θ(k)为极限状态上第 k 次迭代的点。如果式中 X=(x1,x2,……,xn)为任意分布的随机变量,利用上文提到的映射变换法将X当量化为标准正态分布随机变量u=(u1,u2,……,un);
(2)给定 u 和 θ的初始值 u(0)=(u1(0),u2(0),……,un(0))和θ0;
(3)设θ¯为待求的设计参数,将极限状态方程在初值θ0处展开为二阶Taylor公式:

(4)根据给定初始值,计算极限状态方程相应的梯度,同时满足min u=,求得一个新的向量u和新的θ,重复以上计算过程,直至u和θ全部收敛。
3 算例
某天然气管线随机变量的概率分布、均值、标准差及变异系数如表1、表2所示,对其进行可靠度反问题分析[8]。

表1 壁厚8mm管线随机变量分布及验算点

表2 壁厚8mm管线随机变量分布及验算点
解:在内压作用下,管道破坏形式为屈服破坏,根据最大剪应力强度理论(第三强度理论),材料的破坏由最大剪应力引起,其强度条件为:

式中:σθ,σr—管道的周向应力和径向应力;
σe—管道的当量应力;
[σ]—管道的许用应力;
σs—管道的屈服极限。

管道在内压作用下的应力为:

式中:P—管道所受的内压;
Di—管道的内径;
δ—管道的壁厚。
采用改进的一次二阶矩法对相同壁厚不同概率分布的管线进行可靠性分析,经过5次和6次迭代,最终得到可靠度指标分别为β=2.0798,4.1601; 对应的可靠度分 别为 98.08%,99.99%;验算点的迭代最终值见表3。本文主要从下面两种情况对设计参数进行反分析。
情况1:已知天然气管线的可靠度指标β=2.0798,4.1601;假定内压的变异系数为设计参数,其余参数如表1、表2所示。利用前面提出的可靠度反问题求解方法计算内压变异系数。设初始值为 0.15,0.16;迭代收敛精度为 10-4。 分别经过 62、65次迭代,结果收敛至要求精度,迭代的终值分别为 0.1094,0.1256; 其余随机变量的迭代如表 3所示。为了检验计算精度,采用改进的一次二阶矩法对管线结果进行正分析,得到管线的可靠度指标分别为 β=2.0784,4.1593;对应的可靠度分别为 98.08%,99.99%。

表3 情况1迭代结果
情况2:已知天然气管线的可靠度指标,4.1601;假定管道的屈服强度均值为设计参数,其余变量如表1、表2所示。利用可靠度反问题的求解方法计算屈服强度均值,初始值分别为426.7584,423.0000;分别经过 54、63 次迭代,结果收敛至要求精度,各随机变量的迭代结果如表4所示。 迭代最终值分别为 423.5945,420.9458。 为了验证其精度,采用改进的一次二阶矩法对管线结果进行正分析,得到管线的可靠度指标为,4.1587;对应的可靠度分别为 98.08%,99.99%。
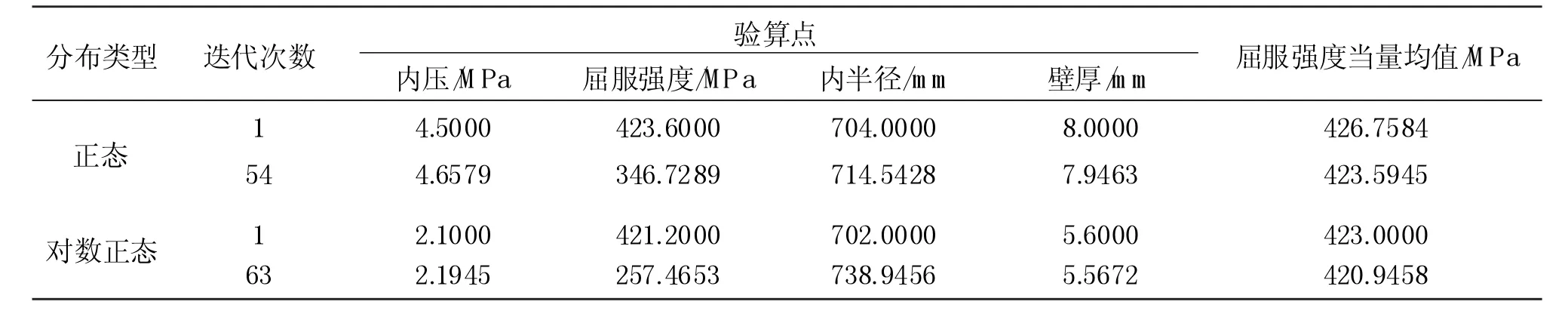
表4 情况2迭代结果
4 结论
(1)以天然气管线为例进行可靠度反分析,并用一次二阶矩法进行验证,结果表明可靠度反分析法的计算精度较高,收敛速度较快;可靠度反分析法也适用于管道参数的计算。
(2)可靠度反分析法具有普遍意义,并有待于进一步研究,应用到其它设备参数的确定中。
[1] 刘强,王树立,赵会军,等.原油顺序输送管道寿命的分析研究[J].石油机械,2007, 35(4):22-24.
[2] 沙丽新,石雪飞.斜拉桥主梁静力可靠性反问题分析[J].哈尔滨工业大学学报,2004, 36(2):258-260.
[3] 马科,丁德馨.可靠度反问题分析方法在地下软岩工程中的应用[J].工程建设与设计,2007,(5):92-94.
[4] 赵事,蒋晓斌,高惠临.腐蚀管道的失效和剩余寿命预测方法[J].油气储运,2006,25(12):28-31.
[5] YANG Kun,ZHANG Xin.Fuzzy Random Reliability Analysis of Blocky Rock-Mass in Slopes[J].China Univ.of Mining & Tech,2005,15(2):129-134.
[6] 罗辉,杨仕教,喻清,等.断裂、基于 FEMA-RSM-GA的边坡锚杆设计可靠性反问题研究[J].武汉理工大学学报,2010, 32(9):93-96.
[7] 李早,赵树德.基于可靠性理论的岩土工程反分析设计[J].西安建筑科技大学学报(自然科学版),2006,38(2):159-177.
[8] 董玉华,余大涛,高惠临.Monte-Carlo法计算含缺陷油气输送管线的失效概率[J].机械工程学报,2004,40(2):136-140.
