关于四元数体上矩阵对角化的几个定理

韦刚和

（盐城生物工程高等学校机械工程系，江苏盐城 224051）

关于四元数体上矩阵对角化的几个定理

韦刚和

（盐城生物工程高等学校机械工程系，江苏盐城 224051）

近年来矩阵对角化理论研究得到了充分的发展，并且在分析方法、研究领域、研究的深度和广度上都有了突破.但在四元数体上，由于四元数乘法的非交换性，人们对四元数体上矩阵对角化的研究甚少.对四元数体上矩阵对角化进行研究，得到了几个重要结论.

四元数体；矩阵对角化；定理

1 引言与符号约定

矩阵对角化问题不仅可解决数学中的非线性规划问题、数学计算问题等，而且在计算物理、量子力学中都有重要的应用.矩阵对角化理论研究近年来得到充分的发展，并且在分析方法、研究领域、研究的深度和广度上都有了突破[1-5].但在四元数体上，由于四元数乘法的非交换性，人们对四元数体上矩阵对角化的研究甚少.本文对四元数体上矩阵对角化进行了研究，得到了几个重要结论.

文中，用R表示实数域，Q表示实四元数体，Qm×n表示m×n阶四元数矩阵的全体，Qn×n表示实四元数体Q 上n阶矩阵的集合，SCn（Q）表示自共轭四元数矩阵全体，Qn表示Q上n维右列空间，用A＊＝-A′表示A的共轭转置.

2 基本概念

定义1设Q是一个实四元数体，A∈Qn×n，如果存在四元数0≠a∈Q与n维非零列四元数向量α，使得Aα=α·a，称a是A的一个右特征值，α为A的对应于右特征值a的右特征向量；如果存在四元数0≠b∈Q与n维非零列四元数向量β，使得Aβ=b·β，称b是A的一个左特征值，β为A的对应于左特征值b的左特征向量[6].

定义2设矩阵A∈Qn×n，如果A＊＝A，则称矩阵A为四元数自共轭矩阵.

定义3设A∈Qn×n，如果A*A=AA*，则称A为四元数正规矩阵.

定义4设矩阵A∈Qn×n，如果A＊A＝AA＊＝In，则称矩阵A为四元数酉矩阵.

定义5设矩阵A,B∈Qn×n，如果存在酉矩阵U∈Un×n，使得B＝U-1AU，则称矩阵A与矩阵B是酉相似.

3 两个重要引理[7]

引理1设矩阵A∈SCn（Q），则存在酉矩阵U∈Un×n，使得

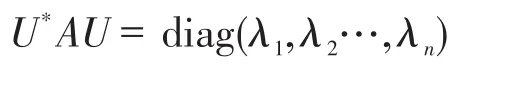
其中λ1，λ2…，λn∈R.

引理2设矩阵A=(aij)∈Qn×n，则矩阵A为正规矩阵的充分必要条件是矩阵A酉相似于对角阵，即存在酉矩阵U∈Un×n，使得

其中λ1,λ2,…,λn∈C，且为矩阵A的n个右特征值.

4 主要结果

定理1设矩阵A为n阶自共轭四元数矩阵，矩阵B为n阶正规四元数矩阵[8].则存在n阶广义酉矩阵U，使U*AU与U*BU都为对角矩阵的充要条件是AB=BA.

证明先证必要性：存在n阶广义酉矩阵U，使U*AU与U*BU都为对角矩阵，即存在酉矩阵U∈Un×n，使得

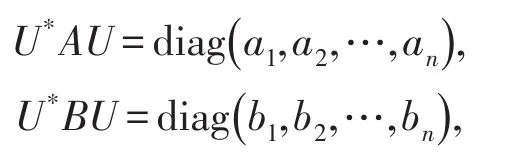
其中a1,a2,…,an为矩阵A的特征值，b1,b2,…,bn为矩阵B的n个右特征值.根据引理1和引理2知道，a1,a2,…,an为实数，b1,b2,…,bn为复数.从而有

得AB=BA.

再证充分性：因为矩阵A为n阶自共轭四元数矩阵，则存在酉矩阵U1∈Un×n，使得

为了方便起见，把相同的特征值进行合并，不妨设合并后的式子为

其中a1,a2,…,as(s≤n)为互不相同的实数.这时我们记矩阵B0=BU1，则显然矩阵B0是正规矩阵.由于AB=BA，易知A0B0=B0A0.令B0=(Bij)为与A0分法相同的分块矩阵，由A0B0=B0A0，知：

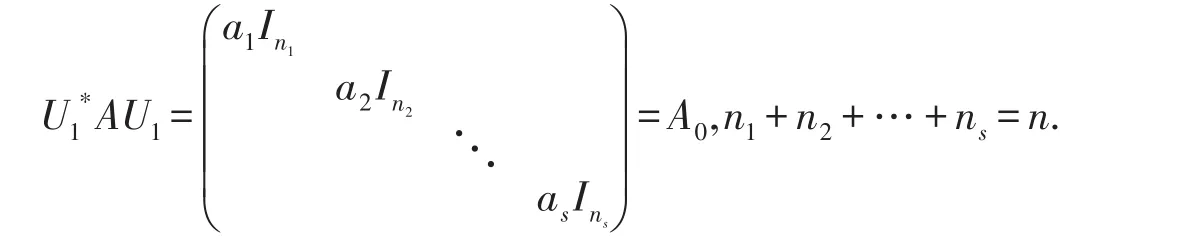
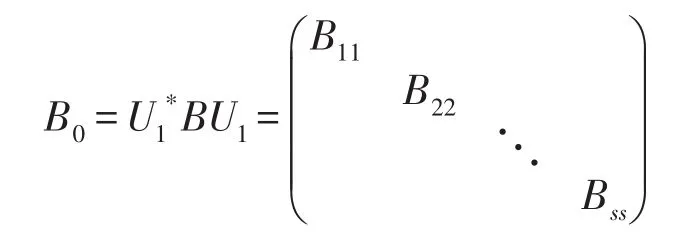
由于B0是正规矩阵，则有Bii() i=1,2,…，s均为正规矩阵，由引理2知，存在四元数酉矩阵V1,V2,…,Vs，使得

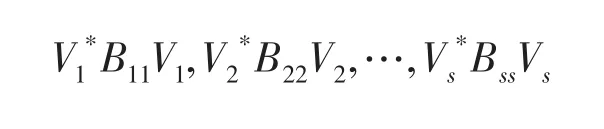
均为复对角矩阵.

这时取

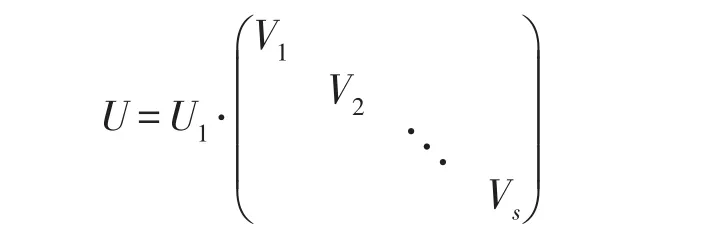
则对于矩阵B有

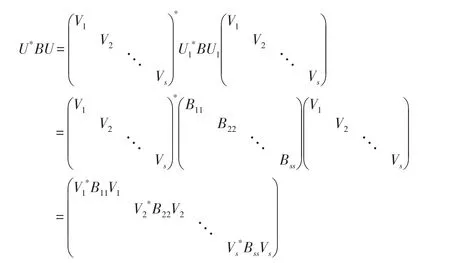
对于矩阵A有

从而，矩阵U*AU也为对角矩阵.

定理2设矩阵A,B均为n阶自共轭四元数矩阵，则存在n阶广义酉矩阵U，使U*AU与U*BU都为对角矩阵的充要条件是AB=BA.

证明因为自共轭四元数矩阵必是正规矩阵，从而根据定理1，定理2得证.

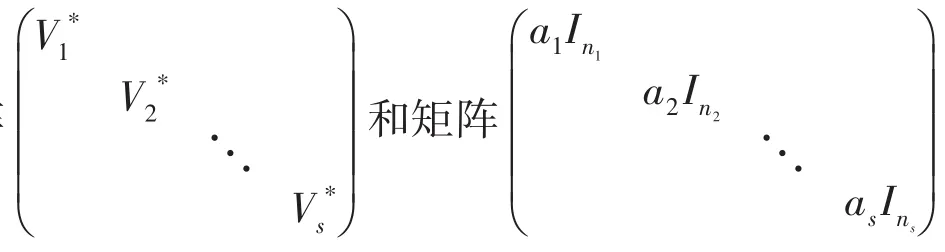
定理3设矩阵A,B为Qn×n上的自共轭矩阵，且矩阵B正定，则有可逆矩阵P∈Qn×n，使得

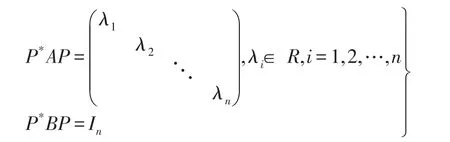
证明由于矩阵B是四元数自共轭正定矩阵，则存在可逆矩阵P0∈Qn×n，使得

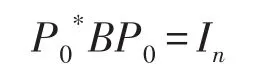
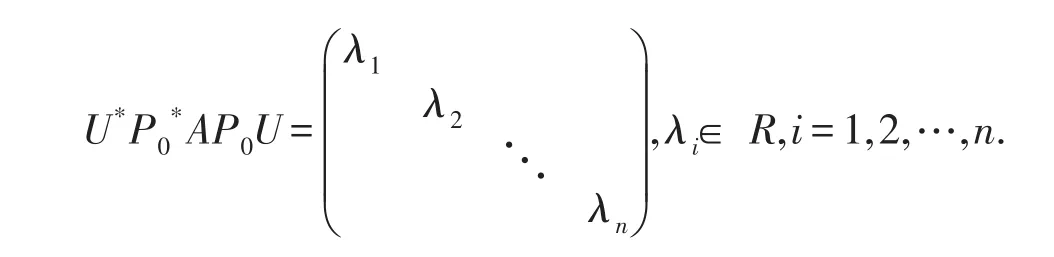
令P=P0U，则P可逆，且

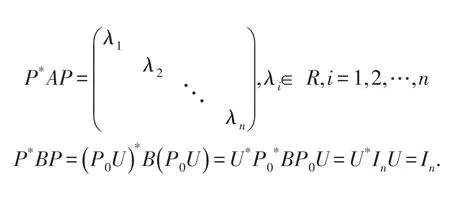
[1]庄瓦金.体上矩阵理论导引[M].北京：科学出版社，2006.

[2]李文亮，四元数矩阵[M].长沙：国防科技大学出版社，2002：6.

[3]屠伯埙.正性除环上矩阵的正定自共轭分解[J].数学杂志，1989（3）：11-16.

[4]屠伯埙.四元数矩阵的UL分解[J].复旦大学学报（自然科学版），1989（2）：45-49.

[5]庄瓦金.四元数矩阵的特征值与奇异值不等式[J].自然杂志，1989（4）：27-32.

[6]姜同松，陈丽.四元数体上矩阵的广义对角化[J].应用数学和力学，1999，20（11）：1203-1210.

[7]庄瓦金.四元数矩阵的极分解及其GL偏序[J].数学进展，2005（2）：5-9.

[8]陈龙玄.四元数矩阵的Jordan标准形[J].应用数学和力学，1996（6）：581-585.

Several Matrix Diagonalization Theorems on the Quaternion

WEI Gang-he
(Department of Mechanical Engineering,Yancheng Higher Vocational School of Biological Engineering,Yancheng 224051,China)

In the recent years,matrix diagonalization theoretical research has been fully developed,and has achieved a breakthrough in the analysis methods,research areas,the depth and breadth of research.But on the Quaternion body,the quaternion multiplication is non-exchangeable,and there has been little study of matrix diagonalization on the quaternion.In this paper,some study is made of the quaternion matrix diagonalization,and several important conclusions are reached.

the quaternion matrix;diagonalization;theorem

O151

A

1008-2794（2012）10-0037-04

2012-09-12

韦刚和（1974—），男，江苏盐城人，讲师，硕士，研究方向：微积分.