挖掘习题教学广度深度提升课堂实效

■胡志奎

挖掘习题教学广度深度提升课堂实效

■胡志奎

所谓课堂教学的广度，是指课堂教学横向上的容量与范围。课堂教学的深度则是指纵向上的教学思考。有广度和深度的课能引发学生深层次的思考，激发学生学习兴趣，培养创新意识和实践能力。教学中，教师要充分挖掘习题教学的广度和深度，激发学生参与学习，提高课堂教学的实效性。

一、案例描述

对一道数学中考试题的探究。

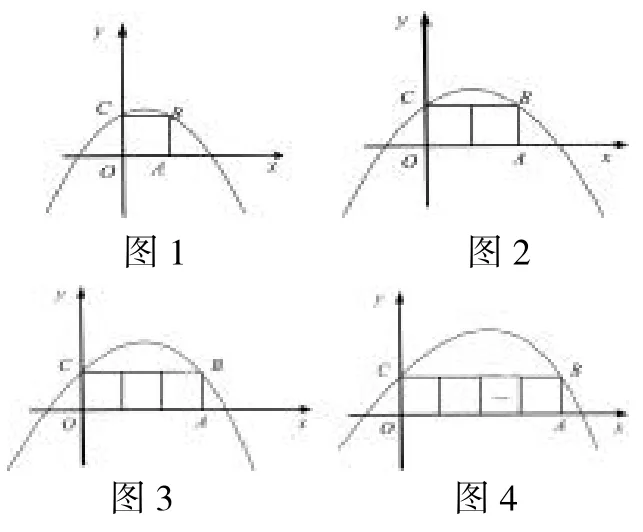
探究一：在平面直角坐标系中，如图1，将1个边长为1的正方形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=-x2+bx+c过正方形顶点B、C.请求出b的值。

分析：本题第一个图形，大部分学生能自己独立完成，先得到点C的坐标，然后求出点B的坐标，这样就可以用待定系数法求得b的值，依次类推，学生能用类似的方法解决图2和图3；

但是要解决n个正方形并排放在一起，b=?，很多学生从前三个图形中总结出规律，b=n.

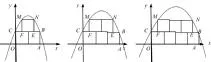
从探究一到探究二老师很自然的通过一个问题过度：如果老师再在上面放一层，同学们想想能否求出函数解析式中的a,b,c的值？呈现题目：

探究二：在平面直角坐标系中，如图（1）所示，在由边长为1的两个正方形组成的矩形OABC的上方作1个同样大小的正方形EFMN,使得EF在线段CB上，如果M、N两点也在抛物线y=ax2+bx+c上，请求出a、b、c的值？按此规律，请归纳在图

（n）中，a、b分别与n的关系

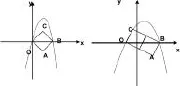
这一探究的关键之处在于如何确定点的坐标？应该选取那三个点？为什么要这三个点而不是其他的点？还要突破B、C以及M、N两点分别关于对称轴对称这一难点。这些都让学生自己去回答，老师只是启发引导，把课堂还给学生，让全体学生都能参与到解决问题中来。其中有学生提出可以在第三层再放一个正方形。这时老师可请同学们思考可以再放一个吗？如果放上去，那么最上面这两个点会在抛物线上吗？请同学们写出坐标，并验证结论是否成立？接下来，如果把正方形顺时针旋转到对角线在X轴上，使抛物线经过O、B两点，是不是还能求出相应的系数呢？

探究三：将图中边长为1的正方形OABC绕点O顺时针旋转，使顶点B落在x轴的正半轴上，设抛物线y=ax2+bx+c同时经过原点O及点B、C，请求出a的值？

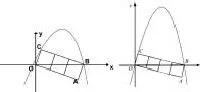
二、案例评析

本节课，最为突出的特点就是对数学习题进行了挖掘，对原来试题中的每一个小题都作了深入的思考和探究，拓展出三个类似的探究题，层层递进，题目设置符合学生的认知规律，由浅入深，循序渐进。注重一题多解，把学生的思维一步一步的展开，呈现出学生对问题解决的过程。找规律题最重要的是从特殊到一般，归纳总结后，又对此做出验证，甚至是证明。教师将观察、类比、猜想、实验、推理、转化等思维过程呈现得淋漓尽致，并且在这一过程中，教师给予了学生较多体验解答计算是否正确的机会，教师也对必要的解答过程也作了清晰的板书，师生合作交流配合很好。

三、案例反思

1．教学设计，强化典型示范

教师在进行复习课程教学中，必须摒弃就题论题的教学，必须树立中考试题往往具有代表性、典型性、示范性，在复习阶段选用中考试题进行课堂教学，可以体现教学的价值性和拓展性，因此需要教师善于对试题进行分析研究。对一道典型试题抽象出简单的具有代表性的试题类型，让学生主动积极参与解决问题的过程，能够从广度上去研究一道试题，展开学习。让学生在解题过程中让把知识点系统化，把分散的知识串起来。培养学生思维的广度要强化一题多解，重视一题多变。训练学生思维的深度，要培养学生追根溯源的习惯，并注重知识的系统性。

2．注重主体，强化学生感悟

基于上述教师的引导，学生在观察、类比、思考、猜想、验证、推理、转化过程中，不仅感受到，数学原来可以这样轻松的学，不知不觉的一节课结束了，认识到研究、思考数学问题的一般思路和方法，做题要及时总结，找规律题的一般方法学生也明白了，所以学生在解决第三问：要求回答n个正方形组成的矩形的对角线放在X轴上，直接写出a的值时，也能先研究一个，再研究二个、三个等特殊到一般的归纳，自然顺畅、水到渠成。这样，学生的所感所悟以及依附于解决问题之上的数学思想方法，具有很强的可迁移性。

3．提升能力，强化典型建构

题目的一系列问题的解决都可以引导学生构建模型，并抓住模型特征，或者在问题解决以后上升到模型的高度，归纳反思解题的方法。波利亚指出：“学习任何东西最好的途径是自己去发现。”数学解题是一种创造性的活动，教师无法教会学生做所有的题目，但可以通过有限题目的学习去领会无限道题的数学机智，深刻感悟解题方法，快速提升解题能力，启迪学生的数学智慧，培养学生创新意识，提高学生的数学素养。

（作者单位：浙江省金华市外国语学校）

责任编辑 王爱民