2D雷达与3D雷达航迹关联问题研究

熊 伟，孙宇宸，高 峰

（1.海军航空工程学院电子信息工程系，山东 烟台 264001；2.中国航天科工集团四院，北京 100854）

雷达组网充分利用各个雷达的资源和信息融合优势，借助通信手段连接成网，由中心站统一调配，通过多个雷达之间的协调和性能互补的优势，克服了单个雷达的不确定性，提高了整个组网系统的整体作战能力。但其前提是各个雷达之间数据必须要进行有效的航迹关联。航迹关联是多目标跟踪系统中的关键环节，是进行目标航迹融合、状态估计以及态势评估的基础，航迹关联的是否精确直接影响整个系统的性能[1-5]。

航迹关联模型一般要求同时对2部或2部以上雷达进行航迹关联，并且雷达的量测维数必须一致。现实的雷达网中装备着大量的2D雷达，但又经常存在其他种类和性质的雷达，典型的情况是2D雷达与3D雷达同时对目标进行观测。如何将2D雷达和3D雷达的信息进行有效地航迹关联，以便在融合中心获得更为精确的目标状态估计，这是目前许多多雷达系统需要解决的一个重要问题[6-9]。

本文通过建立1部2D雷达与1部3D雷达对目标观测的几何模型，采用2D雷达升维来达到维数匹配的问题，从而解决2D雷达与3D雷达的航迹关联问题。

1 升维法

1.1 赋给仰角升维

1)粗关联。

2D雷达与3D雷达的量测如图1所示，设2D雷达和3D雷达的量测向量分别为：

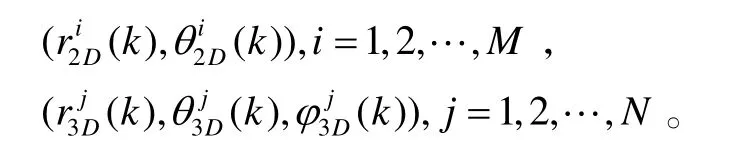
式中，M、N分别代表2D雷达和3D雷达探测到的目标个数，k代表时刻。

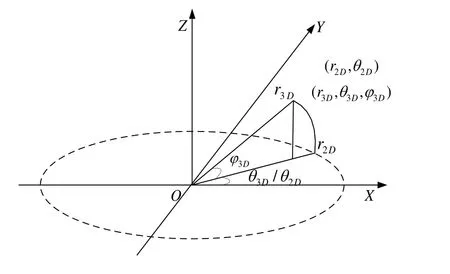
图12 坐标雷达与3坐标雷达的量测

由于2D雷达缺少俯仰信息，所以先从距离和方位信息着手，进行航迹粗关联，挑选出可能关联的粗关联对。对于3D雷达的每一个目标j，通过距离和方位信息，在2D雷达中找到与其粗关联的目标序列 [i∗]，设其长度大小为s=size[i∗]，粗关联的表达式如下：

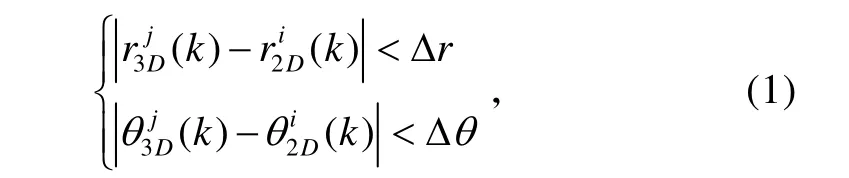
式中，Δr和θΔ为相关波门，可以通过具体的仿真来确定[10]。

通过上式在2D雷达中找到与3D雷达粗关联的目标序列 [i∗]，并把与粗关联目标序列 [i∗]对应的3D雷达的俯仰信息赋给2D雷达的粗关联目标序列，这样，2D雷达的量测向量就升到三维，与3D雷达量测向量形成匹配，为下面的航迹精关联做好了准备。

2)精关联。

按上述方法进行粗关联判决，3D雷达航迹集合中的1条航迹可能与2D雷达航迹集合中的多条航迹粗关联成功。然而，每一个量测只能有1个源。也就是说，3D雷达航迹集合中的1条航迹至多只能与2D雷达航迹集合中的1条航迹关联，反之亦然。因此，在粗关联成功之后，将进行航迹精关联，以确保信息相关的准确率。

升维后，2D雷达与3D雷达的粗关联对表示为：

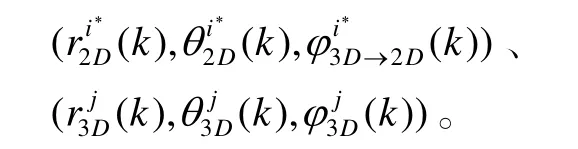
把2D雷达与3D雷达的粗关联对转换到直角坐标系下，得到目标的量测向量分别为：

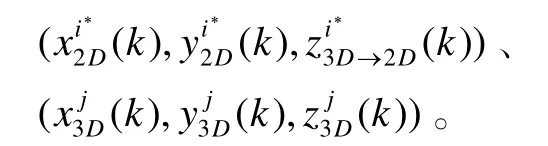
在每一组粗关联对中找出唯一的精关联对，以达到2D雷达与3D雷达航迹关联的目的。

假设2D雷达与3D雷达对同一目标的状态估计误差是统计独立的，利用检验统计量对粗关联对进行精关联检测。

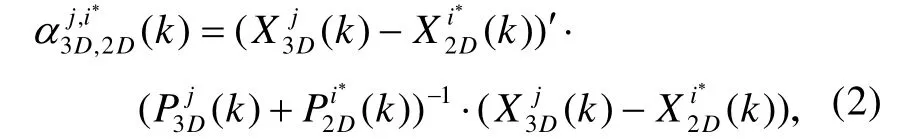
式中：X是状态估计向量；P是状态估计误差协方差。

这里我们构建关联矩阵如下：

在关联矩阵中，粗关联不成功的元素项设为+∞。

在关联矩阵的每一行找出最小的元素且该元素要小于使用χ2分布获得的某一门限，作为每一个粗关联组最终的唯一精关联对，若最小的元素大于门限值，则表明该粗关联组中没有与3D雷达关联的航迹；若小于门限值的最小元素不止一个，则取使航迹间位置差矢量序列的平均范数最小的∗i为最终关联对，即选择使下式成立的∗i为j的关联对，

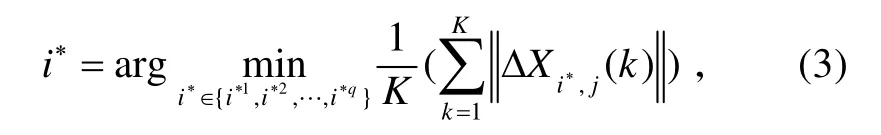
i的编号集合。

赋给仰角升维由于在粗关联中要用到2D雷达与3D雷达距离和方位信息的比较，所以该法只适用于2D雷达与3D雷达同地配置的情况。

1.2 估算仰角升维

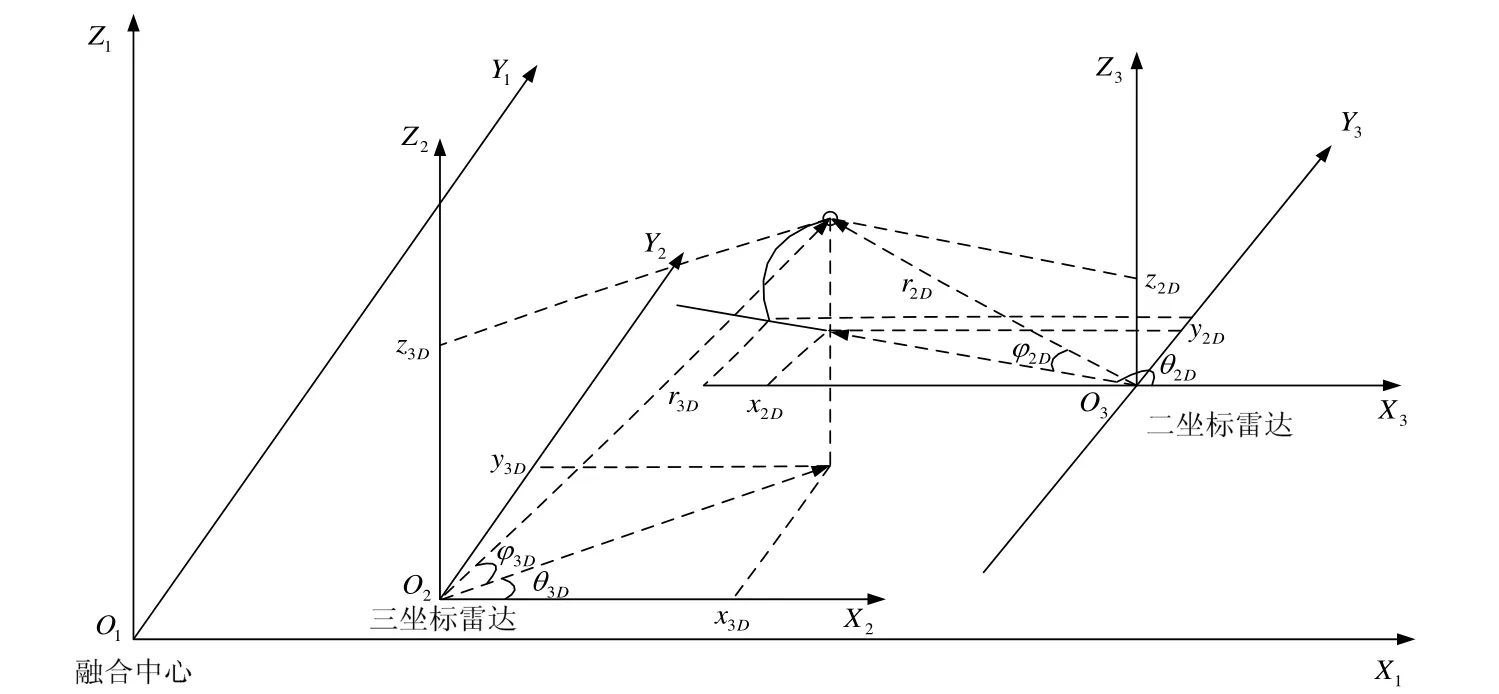
图2 估算仰角与估算高度模型图

对k时刻同一个目标来说，它在地球坐标系下的位置是固定不变的。因此，可以利用这一特性来估算出2D雷达目标测量所缺的俯仰角。

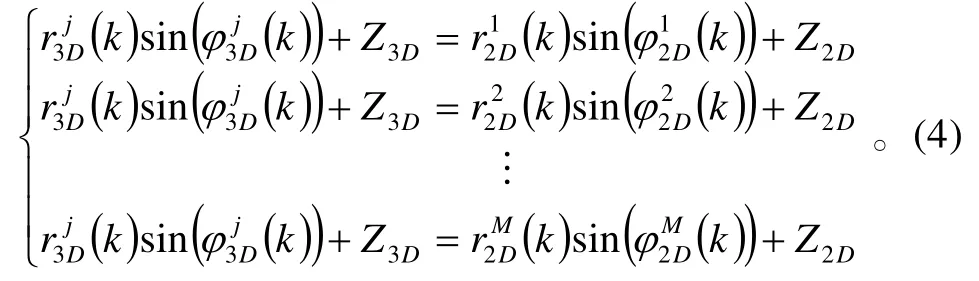
解式(4)得

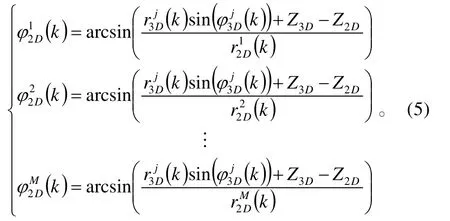
在估算出k时刻3D雷达目标j相对于2D雷达各个目标的俯仰角之后，2D雷达目标的量测向量就表示为由在地球坐标系下，对k时刻同一目标的位置是固定不变的特性，把k时刻3D雷达目标j的极坐标信息转换到直角坐标系下为再转换到地球坐标系下，得到3坐标雷达目标j的量测向量为在地球坐标系下经滤波最 终 得到3D 雷 达的滤 波值然后把2D雷达目标的量测向量转换到直角坐标系下为再转换到地球坐标系下，得到2坐标雷达M个目标量测向量为在地球坐标系下经滤波最终得到2D雷达的滤波值

在得到k时刻3D雷达目标j的滤波值与2D雷达目标M个滤波值后就可以作关联了，2D雷达M个目标的滤波值符合关联规则的，则认为该2D雷达目标与3D雷达的目标j关联。关联时利用检验统计量进行关联检测，

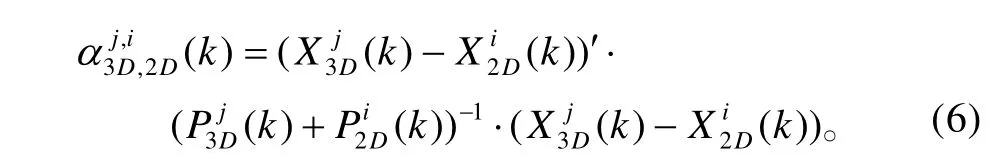
在完成3D雷达目标j的航迹关联后，再重复利用上述方法进行3D雷达其他目标与2D雷达的航迹关联。

从上述的推导可以看出，估算仰角升维既适用于2D雷达与3D雷达同地配置的情况，也可适用于两者异地配置的情况，在不考虑地球曲率影响距离的情况下，有较强的适应性[11]。

2 仿真

2.1 仿真环境

考虑一部2D雷达与一部3D雷达同地配置的情况，坐标均为(2 000 m,3 000 m,5 000 m)，三维空间中20架战机进行匀速直线运动，战机的初始x、y、z位置均在10 000～30 000 m 间产生，战机的初始速度在40～100 m/s 间均匀分布，初始方位角在0～2π间均匀分布，初始俯仰角在0～π/2 间均匀分布。假设2D雷达的测距和测方位角误差为m、3D雷达的测距、测方位角和测俯仰角误差为不考虑雷达系统误差的影响，2部雷达的采样间隔均为T=2 s，用蒙特卡洛方法进行50次仿真，每次仿真时长为N=40 s。仿真时使用搭载Pentium(R)Dual-core E2210 CPU、NVIDIA GeForce 9400 GT 显卡，装有Microsoft Windows XP Professional Service Pack 3系统的电脑。

2.2 仿真结果与分析

图3给出了仿真环境，20架战机在两部雷达的监视区域内做匀速直线运动；图4、5、6分别给出了仿真环境下，2D雷达与3D雷达两种航迹关联算法的正确、错误与漏关联概率，从图中可以看出，估算仰角升维的正确关联概率要高于赋给仰角升维，达到0.988 8左右。此外它的漏关联概率均为0，但是赋给仰角算法的正确关联概率也非常高，相比较估算仰角升维，只下降了1.557 4%。

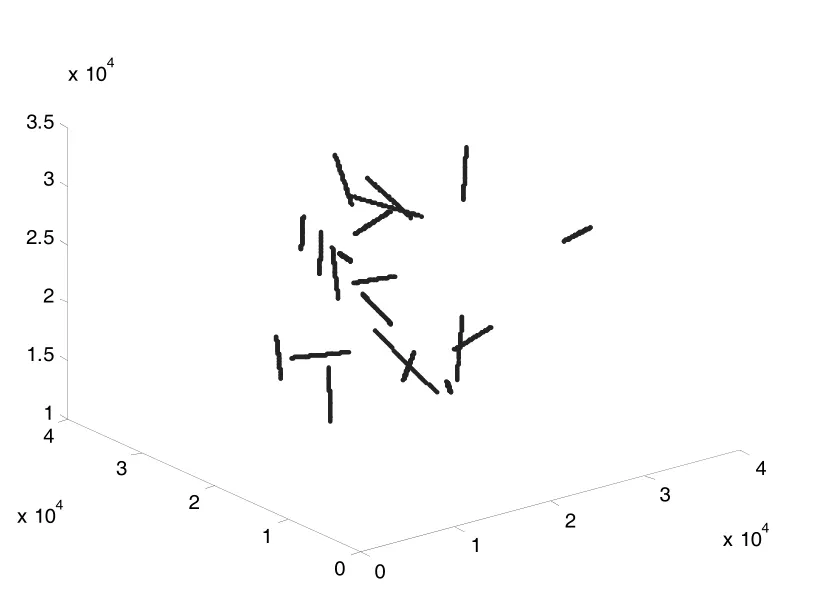
图3 仿真环境

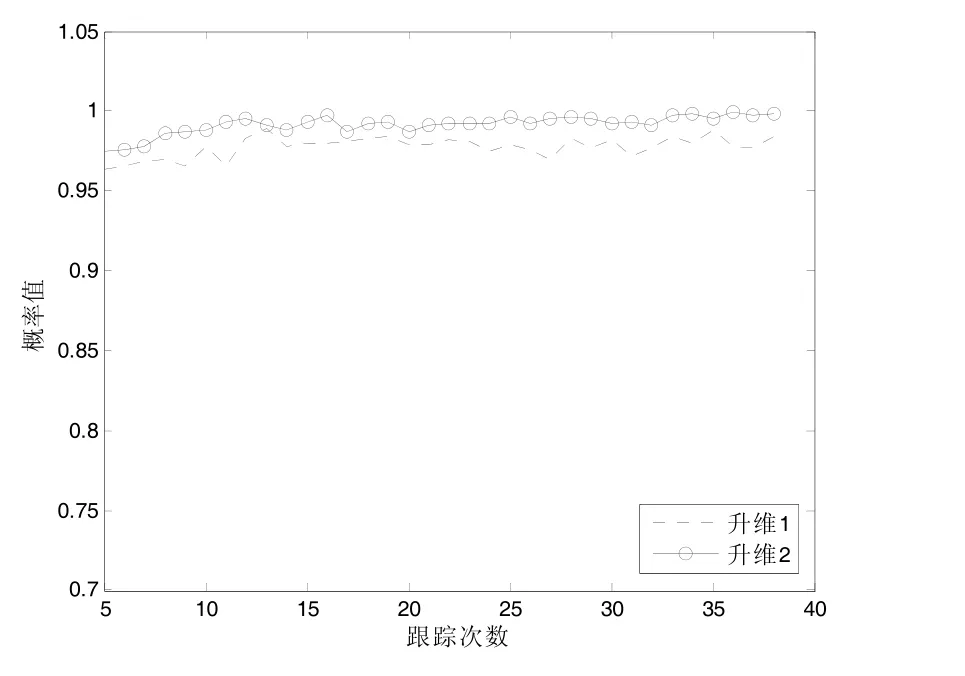
图4 正确关联概率

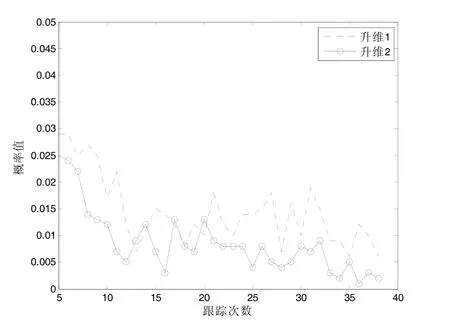
图5 错误关联概率

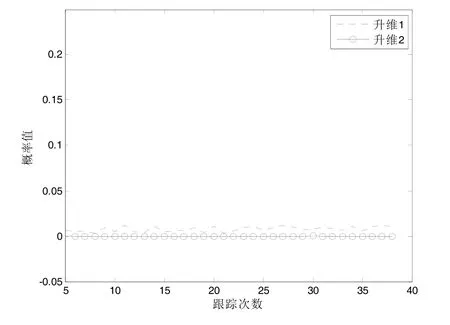
图6 漏关联概率

图7给出了目标批数为20时两种算法耗时比较图，图8给出了算法耗时随目标批数变化图。从图中可以看出估算仰角升维的耗时要大于赋给仰角升维，实时性略不如赋给仰角升维。

图4～8中，升维1代表赋给仰角升维，升维2代表估算仰角升维。

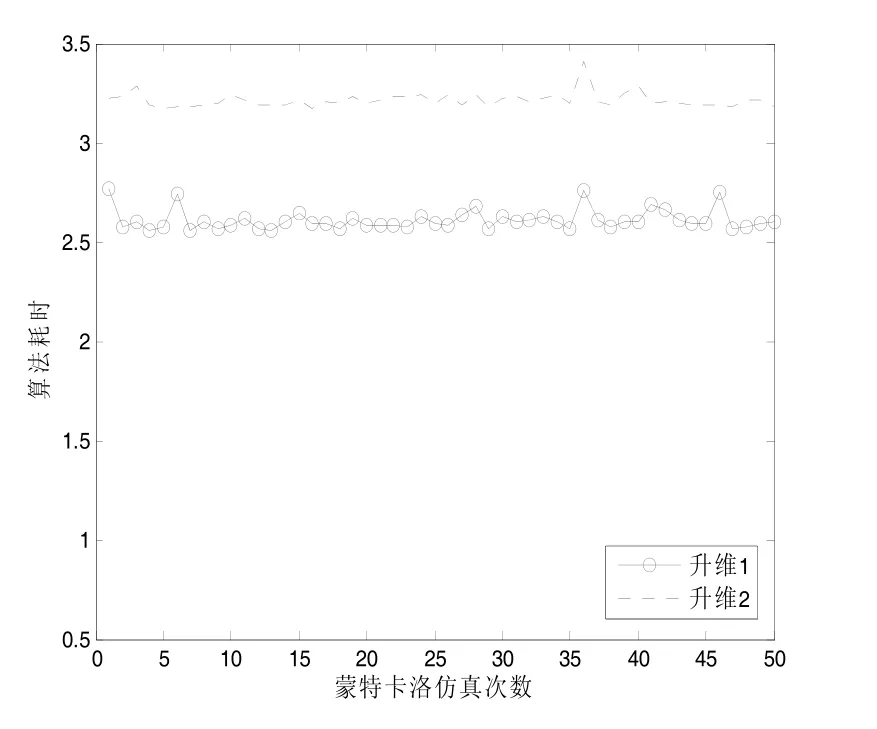
图7 算法耗时比较图

图8 算法耗时随目标批数变化图

表1给出了两种航迹关联算法随目标个数增加的关联概率，从表中可以看出两种关联算法随目标个数的增加下降都很小，相邻目标批数级之间，降幅最大的只有1.32%，两种算法均能维持较好的关联性能，即使是在目标非常密集(120批)的情况下，它们的正确关联概率最低的也能达到92%以上，具有较强的鲁棒性。

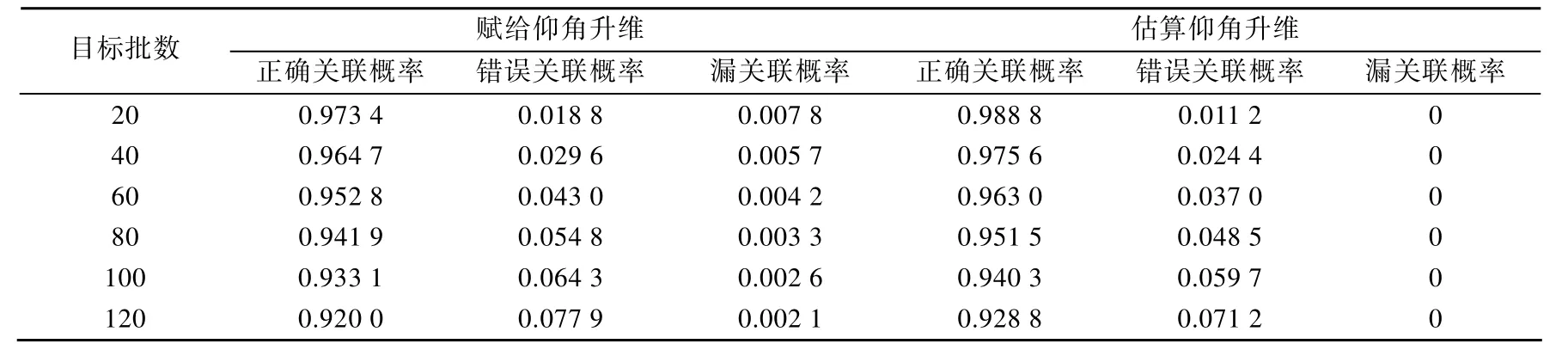
表1 降维法与升维法的航迹关联概率

4 总结

本文针对在工程应用中2D雷达没有俯仰观测，无法直接进行2D雷达和3D雷达航迹关联的问题，通过利用2D雷达升维，以达到维数匹配的目的，从而实现2D雷达和3D雷达的航迹关联。仿真结果表明，本文提出的算法均具有较好的关联效果，且有较强的鲁棒性。但是，如何把升维带来的误差引入到2D雷达和3D雷达的航迹关联中，以进一步提高航迹关联的准确性，是进一步要研究的问题。

[1]BAR-SHALOM Y,WILLIAM D B.Multitarget-Multisensor Tracking,Applications and Advances[M].New York:Artech House,2001:143-147

[2]BAR-SHALOM Y.A Tutorial on Multitarget-Multisensor Tracking and Fusion[C]//IEEE National Radar Conference.New York,1997.

[3]何友.分布式多传感信息融合算法研究[D].北京:清华大学,2006:83-87.

[4]何友,王国宏,陆大惍,等.多传感器信息融合及应用[M].2 版.北京:电子工业出版社,2000:128-183.

[5]王本才,何友,王国宏,等.双战无源均值定位算法精度分析[J].四川兵工学报,2010,31(4):78-81.

[6]徐毓,李锋.不同维状态的多传感器航迹融合[J].传感技术报,2004,17(2):117-121.

[7]何友,熊伟.带反馈分布式不同维传感器状态估计技术[J].宇航学报,2003,24(6):574-578.

[8]张殿程,江晶,陆泳舟.两坐标与三坐标雷达配准方法及其应用分析[J].空军雷达学院学报,2009,23(6):391-398.

[9]高蕊,秦超英,张希彬.不同维状态的多传感器MAP 航迹融合方法[J].昆明理工大学学报,2006,31(3):117-120.

[10]文云峰,石章松,王芳.基于多假设的航迹关联方法研究[J].舰船科学技术,2011,49(2)

[11]朱红绯.地球曲率对双基地雷达定位精度影响的计算机仿真[C]//中国自动化学会第十六届青年学术年会.北京:解放军出版社,2001:641-644.