基于车流动力学理论下城市信号交叉口交通状态的分析

王艺杰 宋 涛

（郑州大学 河南 郑州 450001）

两条或两条以上的道路相交处，称为交叉口，这是车辆与行人汇集和疏散的必经之地，是交能的咽喉。在信号灯的控制下车辆进行有序的停止与通行。在交通流过大的情况下则会出现交通堵塞的现象。1955年，英国学者莱脱希尔和惠特汉提出流体力动力学模拟理论，根据此理论可建立相应的模型对车辆在交叉口红绿灯管制条件下可能出现的车辆是否会产生拥堵及拥堵程度做出合理的分析。

1 分析与建模

在道路上能够自由行驶时车流速度为Vf，当道路上车辆能够自由行驶，车流量达到饱和时，车流速度为Vs，车流密度为Ks，当午车道上流量超过饱和流量后，便会出现阻塞，此时阻塞速度Kj，任意时刻车流密度为K。

假定：当行车道上车流密度K＜Ks时，可认为车辆以饱和状态时的速度Vs行驶，当行车道上车流密度K≥Ks时，则行车速度与车流密度成线性关系。

1933年，格林希尔茨提出，车流速度V与车流密度K之间线性关系，即V＝a－bk，并得出关系式

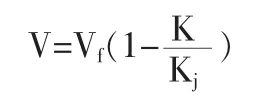
式中：V：行车速度

Vf：畅行速度

K：车流密度

Kj阻塞密度

建模：Hounsel提出车流以自由速度行驶的状态可以保持到当车流量接近饱和流量时。以此为基础，我们建立一种比较接近于实际的半线性关系模型

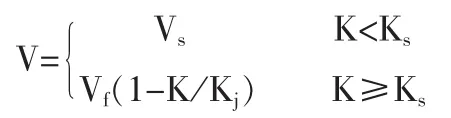
式中：Vs为饱和状态行车速度

Ks为饱和状态下行车密度

V－K关系曲线图如“速度与密度的半线性模型”图所示。

Vs与Ks可通过实验资料予以确定。

2 信号管制下车辆通行状态分析

在任意时刻，车辆到达信号交叉口时的到达流是Q，饱和流量Qs，红灯时间为r,绿灯时间为g。可知

由车流波动理论可知波流量公式为：

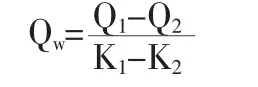
式中：Q1Q2前后两种车流状态的流量

K1K2为前后两种车流状态的密度

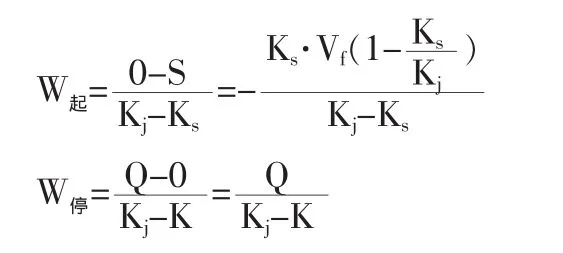
若绿灯时间足够长，则在红灯时间内排除车辆散尽的充分必要条件

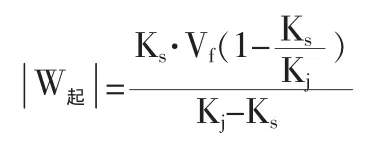
由车辆运行时间-空间轨迹图分析可知：

1）当 K≥Ks时，车辆无法散尽；

2）当K＜Ks时，车辆能够散尽。

则可知，K＜Ks时，即为绿灯时间充足条件下车辆能够散尽的充分必要条件。

在排除散尽条件下，饱和绿灯时间为gs，由

可得

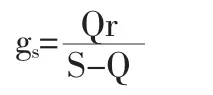
公式修正：根据较多文献资料研究如杨永勤所著交能流三参数关系的研究一文中可知，速度与密度关系曲线如下图“速度-密度关系”所示。

所以采用半线性模型计算拥挤车队消散时间gs时就乘以相应的系数φ，即

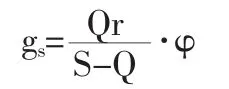
Φ的值可根据大量实验资料进行统计分析拟合而得到，在此不做详细说明。

结论：

1）在车流半线性模型分析下，信号交叉口，车流密度小于饱和车流密度且绿灯饱和时间不小于时，信号交叉口不致出现拥堵现象。

2）在车流半线性模型分析下，若信号交叉口车流密度大于饱和车流密度或绿灯饱和时间小于时，信号交叉口会出现车辆拥堵现象。

3 结语

在半线性车流模型分析下，合理解释了信号交叉口的车辆，因信号灯时间及车流量等因素的影响从而产生拥堵现象的实质原因，为信号交叉口平面设计、交叉口信号控制提供参考。

［1］任福田.交通工程学[M].人民交通出版，2008.

［2］杜贞斌.交通流的流体模型理论[J].江苏大学学报：自然科学版，2002（2）.

［3］徐循初.城市交通与道路规划[M].中国建筑工业出版，2007.

［4］杨少伟.道路勘测设计[J].人民交通出版，2009.

［5］杨永勤.交通流三参数关系的研究[J].北京工业大学学报，2006（32）.