基于脉冲积累的LFM 脉冲调制斜率的ML 估计方法

汝小虎,王 聪,李 悦,姜文利

(1.国防科学技术大学 电子科学与工程学院, 长沙410073;2.海军航空工程学院 电子信息工程系,山东 烟台264000;3.解放军61541 部队, 北京100094)

1 引 言

线性调频信号作为一种大时宽-带宽积信号在脉冲压缩雷达中有重要的应用,准确估计出它的参数对雷达的干扰和个体识别等有重要意义。

已有很多文献研究了LFM 信号的参数估计问题,包括T.J.Abatzoglou 提出的载频和调制斜率联合估计的ML 方法[1]、P.M.Djuric 等人提出的解相位方法[2]、S.Peleg 等人提出的离散多项相位变换(Discrete Polynomial-Phase Transform, DPT)方法[3],以及基于chirp 傅里叶变换方法[4]等。但是这些研究都只针对一个信号,当信号信噪比较低时,其性能会受到很大影响。如解相位方法的信噪比门限为8 dB左右,DPT 方法在信噪比为0 dB时估计方差会比克拉美-罗限(Cramér-Rao Lower Bound, CRLB)高出约60%。文献[5]和[6]分别改进了解相位方法和DPT方法,但对调制斜率估计精度的提高程度有限。另外,这些LFM 信号参数估计方法常常要在离散的频域或二维平面上进行极值搜索,其准确度和时间效率无法兼顾。

在实际环境中截获到的具有相同调制波形的雷达脉冲不止一个,而且对LFM 信号感兴趣的往往只是它的调制斜率。但是针对多个LFM 脉冲信号的调制斜率估计问题,尚未发现有文献提出解决方法。本文提出的方法首先基于脉冲积累得到信噪比较高的调制波形估计,接着解出相位,之后用最小二乘法估计调制斜率。其关键步骤是估计调制波形,典型方法是Howard 提出的ML 估计方法[7],本文研究了其近似的快速计算方法,给出了其适用条件。本文方法的优势在于可以处理多个脉冲信号,不需要搜索操作,并且经论证是一种最大似然估计方法,参数估计精度高。

2 信号模型

由于数据采集的先后顺序不同和多普勒效应等原因,具有相同调制波形的雷达脉冲会有相对的时延和载频的不一致,脉冲积累的前提是使得脉冲在时间和频率上对齐。假设已实现了理想的时频对齐,用下面的信号模型描述具有相同调制波形的LFM 脉冲:

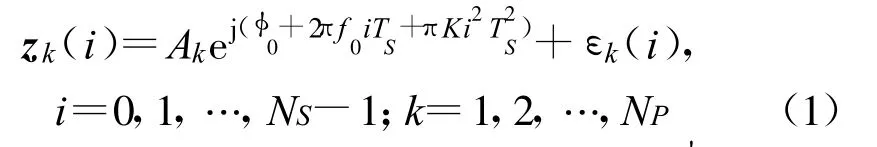
其中,NS为采样点数,NP为脉冲数;Ak=A ejk是幅度因子,它的模A 表示脉冲幅度(对于短时间内截获到的NP 个脉冲,可认为A 对所有脉冲都一样),它的相位k是无用参数,不进行估计;εk是复高斯噪声,满足E(εk)=0 ,E(εkεHk)=2σ2I,其中2σ2为噪声功率,I 为单位矩阵;0、f 0 和K 分别为相位调制

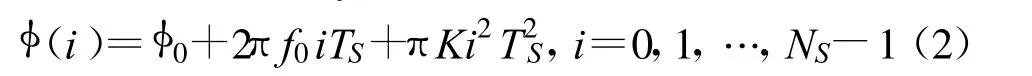
的初相、载频和调制斜率,其中TS为采样间隔。

由于调制波形的ML 估计结果不可避免地会有初相存在,所以式(1)中的信号模型认为相位调制存在初相,它并不影响调制斜率的估计。该信号模型中,未知参数是{A,0,f0,K},本文关心的是调制斜率K 的估计。

3 基于脉冲积累的LFM 脉冲调制斜率的ML 估计方法

3.1 调制波形估计

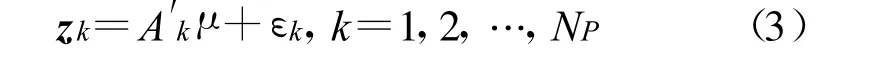
其中A′k= NSAk。式(3)中未知参量是复幅度A′k和调制波形μ,NP个脉冲zk的联合概率密度函数为

将式(4)中的求和项作如下变形:

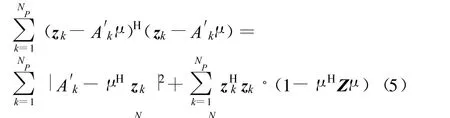
由瑞利准则[8]可知,当μ是Z 矩阵最大特征值对应的特征向量时,式(5)中μHZμ达到最大。所以调制波形的ML 估计 μ是Z 矩阵最大特征值对应的特征向量。

直接计算矩阵的特征向量会使时间代价很大。文献[7]提到,如果Z 矩阵的最大特征值超过0.5,可以通过迭代的方式快速求得 μ的近似结果,与直接求特征向量得到的结果非常接近。第4 节仿真实验会证实,当脉冲信噪比高于0 dB时可以利用这种近似计算方法。

3.2 调制斜率估计

Tretter 指出,当信噪比较高(8 dB以上)时,观测信号中的加性复高斯噪声可等效为相位上的加性实高斯噪声,并且在高斯噪声条件下最小二乘估计等效于ML 估计[9]。所以,为了提高调制斜率的估计精度,得到调制波形的ML 估计后,用文献[10]提到的基于相对无模糊相位重构的方法解相位得到相位调制的估计 =[ (0), (1), …, (NS-1)]T,然后对它用最小二乘法进行二次曲线拟合估计调制斜率K。设相位调制的理论值为 (i)=a0 +a1 iTs +a2i2T2s,i=0,1, …,NS-1,令a =[ a0,a1,a2]T,对它的估计为

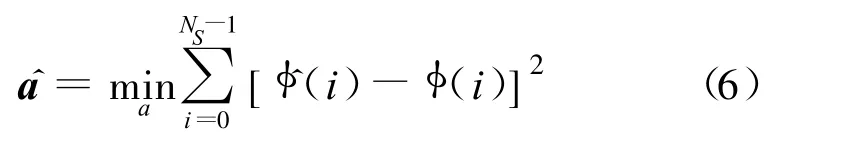
那么调制斜率K 的估计可由 a2/π得到。下面求 a的解析表达式。拟合误差为

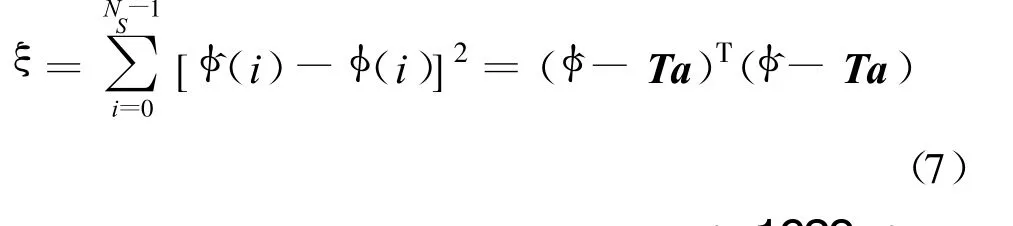
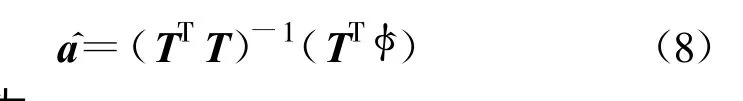
其中矩阵T 为

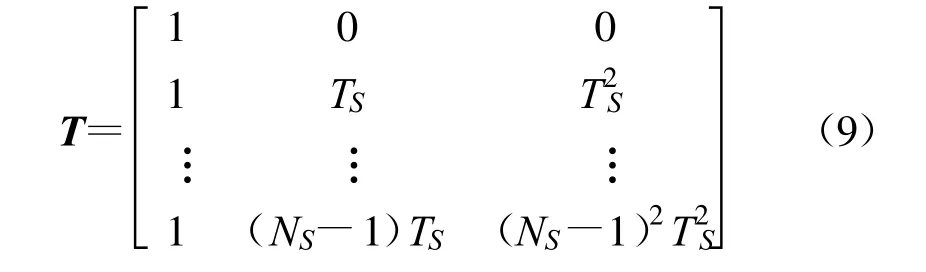
综合以上分析,基于脉冲积累的LFM 脉冲调制斜率的估计方法总结如下。

(1)如果脉冲的平均信噪比低于0 dB,由zk,k =1,2, …, NP构造脉冲积累矩阵Z,求该矩阵最大特征值对应的特征向量,得到调制波形的估计 μ,然后执行第3 步;否则,如果脉冲平均信噪比高于0 dB,执行第2 步。

(2)设zmax为信噪比最大的脉冲,调制波形的初始估计为 μ(0)=norm[zmax] ,其中norm[·]表示归一化。取m =0,重复计算

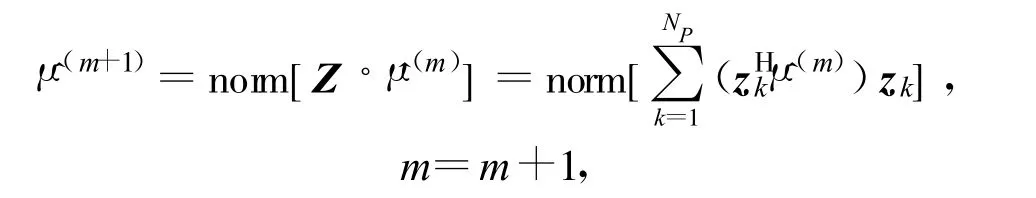
直到

其中β 是个很小的数,比如0.001,调制波形的ML估计近似为 μ≈ μ(m+1)。

(3)用基于相对无模糊相位重构的方法解出 μ的相位 。

(4)由式(8)、(9)计算二次曲线的拟合系数 a,那么调制斜率的估计为 K = a2/π。

3.3 讨论

本节对3.2 节提出的调制斜率估计方法进行讨论,证明该方法是最大似然的。

首先定义函数β=g(v),其中v 是一个幅度固定的信号矢量。函数g 的功能是先解出v 的相位,然后用最小二乘法拟合该相位,得到的二次项系数与π的比值为函数值β。根据3.2 节提出的调制斜率估计方法,有 K =g( μ)。另外,g 是一对一的函数,这是因为如果v 的值发生改变,由于它的模是固定的,所以它的相位会发生变化,由式(8)可知所有的拟合系数都会改变,最后会得到不同的β;另一方面,如果β 发生变化,意味着二次曲线会发生变化,即v 的相位会改变,所以对应不同的v。

如果v=μ,由g 函数的功能可知,调制斜率K=g(μ)。又因为 μ是调制波形μ的ML 估计,由ML 估计的不变性[11]可以推得 K =g( μ)是K 的ML估计,即本文提出的调制斜率估计方法是最大似然的,故将该方法称为基于脉冲积累的调制斜率ML估计方法。

需要说明的是,上述结论成立的前提条件是能准确解出 μ的相位,这就要求 μ有较高的信噪比。本文基于脉冲积累估计调制波形,使得 μ可以满足信噪比要求,第4 部分会对此进行仿真验证。

4 仿真结果与分析

4.1 调制波形估计结果的信噪比

本节先考查脉冲积累矩阵Z 的最大特征值随信噪比的变化。仿真时设脉冲数NP=100,采样率fS=250 MHz,脉冲宽度为2 μs,噪声功率2σ2=2,式(1)中幅度因子Ak的相位在[0,2π] 间随机分布,LFM 相位调制的初相0=π/3,载频f0=40 MHz,调制斜率K=1 MHz/μs。

图1 给出了脉冲积累矩阵Z 的最大特征值随信噪比的变化,其中脉冲信噪比定义为脉冲内信号与噪声平均功率的比值,所以式(1)中脉冲的信噪比为A2/2σ2,图中以dB 作为单位。可以看出,当信噪比高于0 dB时,Z 矩阵的最大特征值大于0.5,可以用ML 方法的近似迭代计算方法。此外,由图1 可知,脉冲数降低会使Z 矩阵的最大特征值增大,而改变采样率对最大特征值的影响很小。

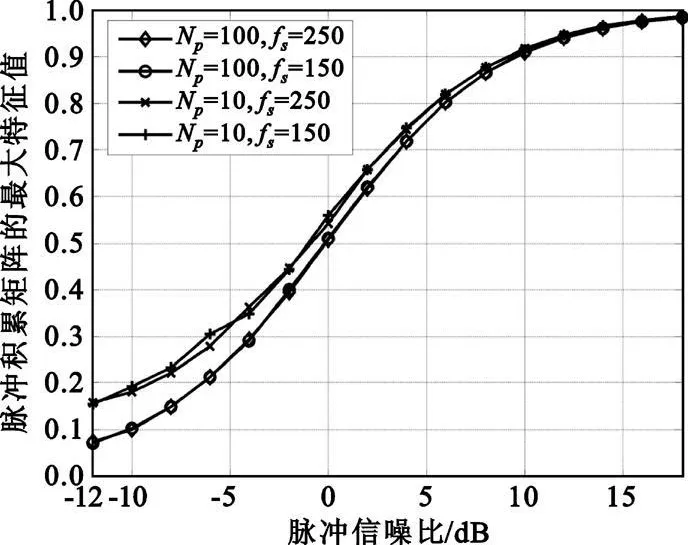
图1 脉冲积累矩阵的最大特征值与脉冲信噪比的关系Fig.1 The biggest eigenvalue of pulse accumulation matrix vs.the SNR of pulses

现在研究调制波形估计结果的信噪比与脉冲信噪比的关系。调制波形的估计为 μ=μ+ε,其中ε= μ-μ认为是估计结果中的噪声,所以调制波形估计结果的信噪比为

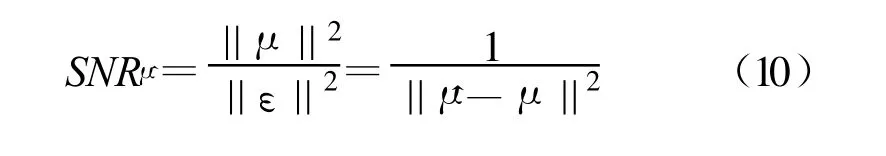
由于 μ相对μ可能会有不同的初相,但是这对后续的调制参数估计没有任何影响,所以在用式(10)研究信噪比之前应该先消除这一初相上的不一致。

用ML 方法估计调制波形μ,脉冲数NP分别设为100、40 和10,其他设置不变,蒙特卡洛仿真200次,得到的调制波形估计结果的信噪比与脉冲信噪比的关系如图2 所示。由图可知,调制波形估计结果的信噪比相对脉冲的信噪比高出约10 lg NP(dB),说明脉冲积累可以大大改善信噪比,有利于准确解出相位调制。

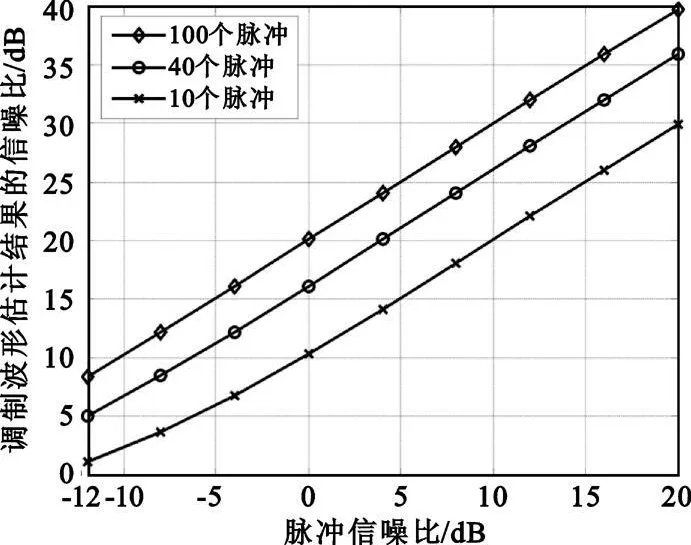
图2 调制波形估计结果的信噪比与脉冲信噪比的关系Fig.2 The SNR of the estimated modulation waveform vs.the SNR of pulses

4.2 调制斜率估计

本节研究不同脉冲数目条件下调制斜率K 的估计方差与信噪比的关系,分析提出的ML 估计方法的门限效应和脉冲积累效果。先给出式(1)信号模型调制斜率估计的CRLB。当脉冲只有一个,即NP=1 时,文献[12]给出了调制斜率估计的CRLB,约为90/(π2N5ST4S·SNR),其中SNR 为脉冲信噪比。对于式(1)中独立同分布的NP个观测数据,参数估计的CRLB 是单次观测的1/NP倍[11],所以脉冲积累条件下LFM 脉冲调制斜率估计的CRLB 为调制斜率的估计方差为

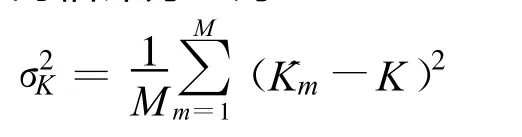
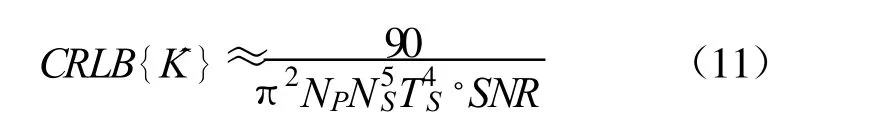
其中,M 为蒙特卡洛仿真次数, Km为第m 次仿真对调制斜率K 的估计。脉冲数NP分别设为1、10 和40,蒙特卡洛仿真次数为200 次,其他设置与4.1 节相同。得到的调制斜率估计方差与脉冲信噪比的关系曲线如图3 所示,其中纵坐标为10 lg(σ2K)。可以看出,本文提出的调制斜率估计方法存在门限效应,并且利用的脉冲数目越多信噪比门限越低。对于只有一个脉冲的情况,当信噪比在8 dB左右时调制斜率的估计方差就迅速偏离了CRLB;而对于40 个脉冲的情况,当信噪比在-5 dB左右时估计方差仍能达到CRLB。这说明本文提出的调制斜率估计方法可以在低信噪比的情况下大大降低估计方差,具有优越的性能。

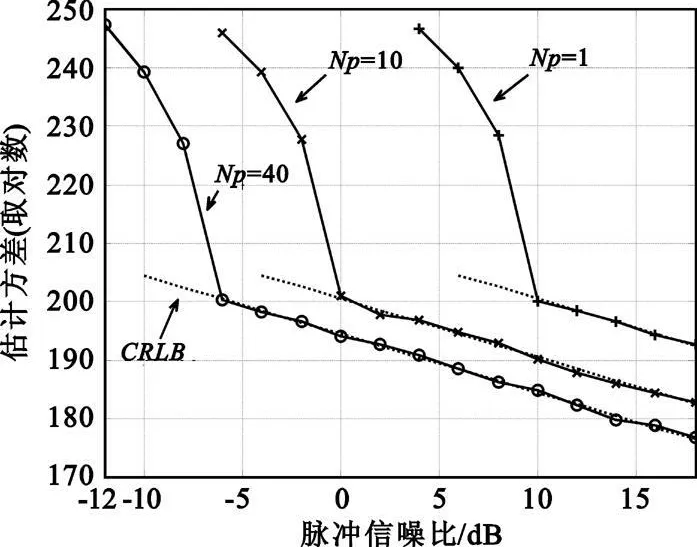
图3 调制斜率估计方差与脉冲信噪比的关系Fig.3 The estimation variance of chirp rate vs.the SNR of pulses

现在进一步研究基于多个脉冲相对基于单一脉冲进行调制斜率估计的性能差异,即脉冲积累的效果。图4 给出了单个脉冲和NP=10 个脉冲两种情况下调制斜率估计方差的比值(设这个比值为γ)与脉冲信噪比的关系,其中纵坐标表示10 lg(γ)。可以看出当信噪比较高时, γ基本不随信噪比变化,实际上此时γ应该等于NP,即NP 个脉冲联合估计相对单个脉冲的估计使得调制斜率的估计方差降低了NP倍;而当信噪比较低时,估计方差降低的倍数远超过NP。比如对于4 dB的情况,相对于单个脉冲,由10 个脉冲对调制斜率进行估计使得估计方差降低了γ≈105倍,脉冲积累效果明显。

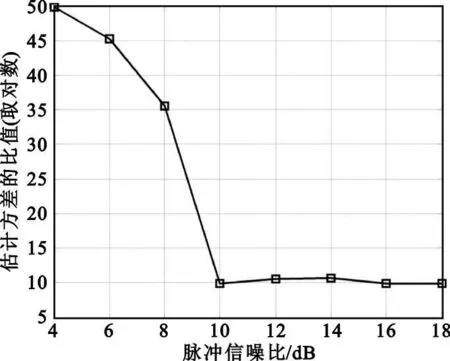
图4 单个和10 个脉冲条件下调制斜率估计方差的比值与脉冲信噪比的关系Fig.4 The ratio of the estimation variance of chirp rate under conditions of a single pulse and 10 pu lses vs.the SNR of pulses

5 结 论

本文利用多个脉冲对LFM 脉冲信号的调制斜率进行估计,提出了一种经论证是最大似然的估计方法。该方法首先由脉冲积累估计出调制波形,大大改善了信噪比,进而准确地解出LFM 脉冲的相位,然后用最小二乘拟合的方法估计出调制斜率。提出的方法在低信噪比条件下可以使得调制斜率的估计方差达到CRLB,具有很低的信噪比门限。

需要指出的是,本文基于的信号模型假设脉冲已经实现了理想的时频对齐,但是在低信噪比条件下脉冲的时频对齐会有较大的偏差,导致调制波形和调制参数估计精度的下降,对这一问题的解决还有待进一步的研究。

[ 1] Abatzoglou T J.Fast maximum likelihood joint estimation of frequency and frequency rate[J] .IEEE Transactions on Aerospace and Electronic Systems,1986,AES-22(6):708-715.

[ 2] Djuric P M, Kay S M.Parameter estimation of chirp signals[ J] .IEEE Transactions on Acoustics, Speech and Signal Processing, 1990, 38(12):2118-2126.

[ 3] Peleg S, Friedlander B.The discrete polynom ial-phase transform[ J] .IEEE Transactions on Signal Processing, 1995, 43(8):1901-1914.

[ 4] Xia X G.Discrete chirp-Fourier transform and its application to chirp rate estimation [ J] .IEEE Transactions on Signal Processing, 2000, 48(11):3122-3133.

[ 5] 金胜, 王峰, 邓振淼,等.一种LFM 信号相位域快速高精度参数估计算法[J] .系统工程与电子技术, 2011,33(2):264-267.

JIN Sheng, WANG Feng, DENG Zhen-miao, et al.Fast and accurate estimator on parameters of chirp signals in phase domain[ J] .Systems Engineering and Electronics, 2011, 33(2):264-267.(in Chinese)

[ 6] 周良臣,杨建宇,唐斌.一种高效的LFM 信号参数估计方法及性能分析[ J] .电子学报,2007,35(6):1128-1133.

ZHOU Liang-cheng, YANG Jian-yu, TANG B.An efficient parameter estimation and performance analysis for LFM signal[ J] .Acta Electronica Sinica, 2007, 35(6):1128-1133.(in Chinese)

[ 7] Howard S D.Estimation and correlation of radar pulse modulations for electronic support[ C]//Proceedings of the 2003 IEEE Aerospace Conference.Big Sky, MT:IEEE, 2003:2065-2072.

[ 8] Horn RA, Johnson, C R.Matrix analysis[M] .Cambridge:Cambridge University Press, 1985.

[ 9] Tretter S A.Estimating the frequency of a noisy sinusoid by linear regression[J] .IEEE Transactions on Information Theory, 1985, IT-31(6):832-835.

[10] 黄知涛, 周一宇, 姜文利.基于相对无模糊相位重构的自动脉内调制特性分析[ J] .通信学报, 2003, 24(4):153-160.

HUANG Zhi-tao,ZHOU Yi-yu, JIANG Wen-li.The automatic analysis of intrapu lse modulation characteristics based on the relatively non-ambiguity phase restoral[ J] .Journal on Communications,2003,24(4):153-160.(in Chinese)

[11] Kay S M.统计信号处理基础——估计与检测理论[M] .罗鹏飞, 张文明, 刘忠, 等, 译.北京:电子工业出版社, 2006.

Kay S M.Fundamentals of Statistical Signal Processing:Estimation Theory and Detection Theory[M] .Translated by LUO Peng-fei,ZHANG Wen-ming,LIU Zhong,et al.Beijing:Publishing House of Electronic Industry,2006.(in Chinese)

[12] Peleg S, Porat B.The Cramér-Rao lower bound for signals with constant amplitude and polynom ial phase [ J] .IEEE Transactions on Signal Processing,1991,39(3):749-752.