沥青混合料有限元断裂分析的网格特性

杜军虎， 韩 丁

（合肥工业大学交通运输工程学院，安徽合肥 230009）

对于沥青混合料疲劳性能的评价，传统方法是通过大量的室内试验获取相关数据，并与相应的规范指标进行比对来分析沥青混合料在不同条件下的疲劳性能［1－3］。由于在试件成型过程中存在一定的误差，试验结果的离散性较大，加之这类试验耗时较长，使得工作量变大且成本提高。相比之下，用有限元软件仿真来替代真实试验有更大的优越性。文献［4］利用扩展有限元法研究了有限元模拟裂纹尖端网格划分的方法；文献［5］用有限元法对沥青路面在初始裂纹形成后的裂纹扩展规律进行了研究；文献［6］利用非线性有限元方法分析了沥青混合料小梁疲劳试验中弯拉应力、挠度、损伤变量、裂纹扩展速率等的变化规律，并预测了沥青混合料试件的疲劳寿命及失稳断裂时的裂纹长度；文献［7］基于黏弹性连续损伤理论用有限元分析法预测了沥青混凝土路面的疲劳性能；文献［8］通过ABAQUS有限元模拟，分析了级配碎石夹层对基层反射裂缝的影响。在有限元软件仿真的过程中，结果的精确性是主要考虑的问题之一。在确定工况下，有限元模型网格密度的大小决定了计算结果的精确性［9］。一般来说，网格越细化，得到的计算结果越精确，但过密的网格划分会以较长的计算时间为代价。确定出合理的网格密度，可使有限元的仿真结果既能满足精确性的要求，又具有合理的计算成本。

本文对沥青混合料小梁弯曲破坏试验进行有限元仿真；应用线弹性断裂力学理论，计算沥青混合料小梁试件梁底张开型裂缝对应的应力强度因子KⅠ值［10－12］和J积分值［13－14］；获取一定试验工况时3种几何尺寸模型在不同网格密度下的KⅠ值及J积分值，分析沥青混合料小梁试件有限元模型的网格密度对计算结果的影响，确定对应不同尺寸试件的合理网格密度，最后利用Matlab软件对所得数据进行交互界面数据库的建立，为使用者提供方便直观的查询。

1 小梁弯曲试验的有限元模拟

1.1 模拟工况

利用有限元软件对50 mm×50 mm× 250 mm、50 mm×50 mm×300 mm、100 mm× 100 mm×300 mm 3种几何尺寸小梁试件的弯曲破坏进行模拟，小梁试样重量分别为0.014 4、0.018、0.072 k N，采用三维有限元模型，模拟三分点加载模式，如图1所示。

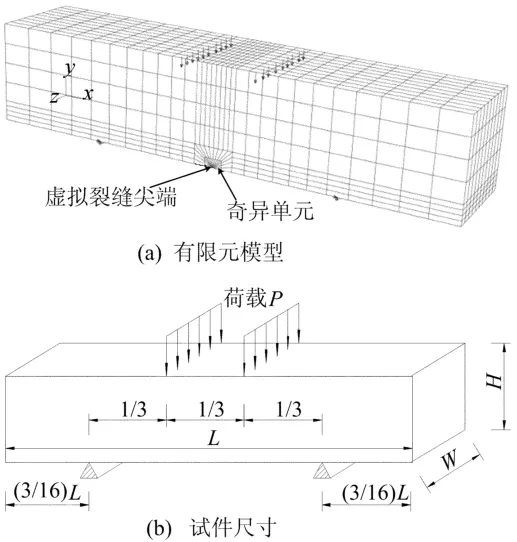
图1 有限元模型及试件尺寸

为了分析网格划分密度对仿真结果的影响，固定加载值大小为8.4 k N，底部两支撑位置距小梁侧面的距离为整个小梁长度的3／16，通过约束支撑位置x、y方向位移自由度来模拟对小梁的支撑。加载位置为支撑间三分点处。

1.2 网格划分及单元类型确定

对于小梁模型的网格划分策略，采用结构化网格划分方法。在通常情况下，小梁产生开裂的位置为底部中间位置，因此该部位是着重关心的区域。如果采用常规单元来划分裂缝尖端附近区域，不论尖端附近的网格划分有多细，计算精度都不会高。一些用于模拟裂缝尖端附近特殊应力、应变场的特殊单元随着有限元的发展相继出现。目前，简洁、常用的办法是直接采用1／4节点单元（奇异单元），即在裂缝尖端处将中间结点向裂缝尖端靠拢，距裂缝尖端1／4边长处，如图2所示，这样的单元可以较好地反映裂缝尖端附近的应力场。因此，在底中部取10 mm×20 mm的区域进行网格细化，并采用奇异单元（图1标注位置）模拟虚拟裂缝尖端的奇异性［15］，以虚拟裂缝尖端为中心向外共设置3个围道。对于其他区域，采用普通的六面体单元，并设置相对较大的网格尺寸，在试件宽度方向划分10层网格单元。这样划分网格既考虑到了小梁底部中间位置计算结果的精确性，同时又能避免对不重要区域的大量无用计算。

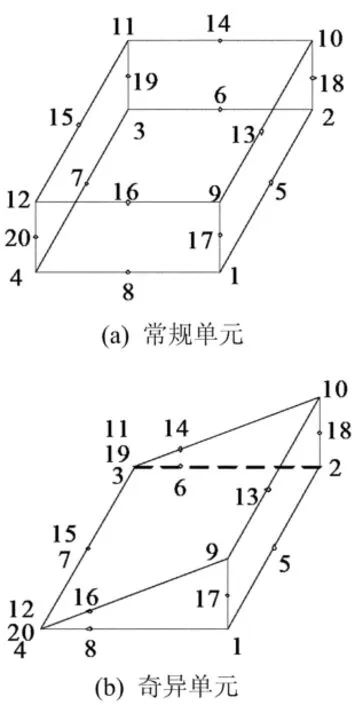
图2 常规单元与奇异单元的比较

除了网格的划分策略，在有限元的模拟中，选用的单元类型对于计算结果同样有很大影响。通常二次完全积分单元对应力的计算结果较准确，适用于模型应力集中问题，且一般情况下不会出现一次积分单元常见的剪力自锁及沙漏等问题［16］。采用奇异单元对沥青混合料小梁的断裂力学指标进行计算时，虚拟裂缝位置会产生应力集中现象［17］，因此适合选用二次完全积分单元。

1.3 计算结果

在一定的模拟试验工况以及网格划分方法下，网格密度是影响输出结果的主要因素。为了寻求合理的网格密度，对3种不同尺寸小梁模型的底中部细化区域分别取12、24、48、96、192个／cm35种不同的网格密度，进行有限元仿真，其中3种网格密度下得到的计算云图经局部放大后如图3所示。

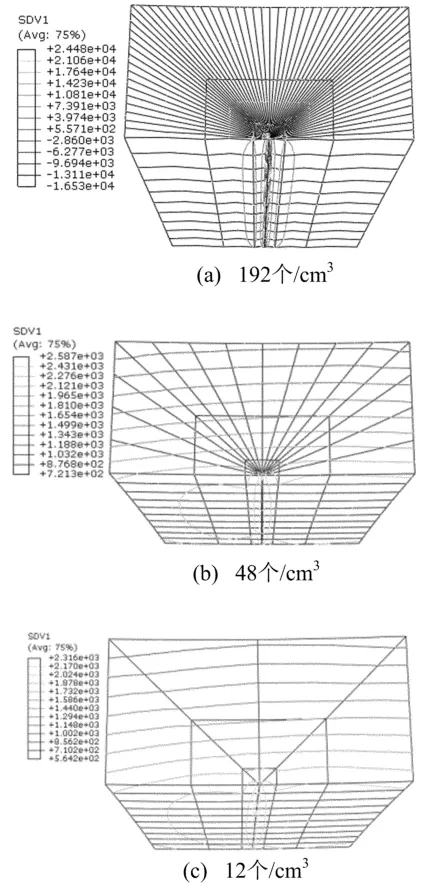
图3 不同网格密度下的计算云图

在有限元模型的奇异单元区域沿试件宽度方向由前向后设置了21层围道，每层围道由内向外又分别设置了3个围道。为了使计算值更具代表性，取中间层围道第2围道的中间点作为数据输出节点。通过计算，得到了3种尺寸（长×宽×高）数值试件在不同网格密度下该节点的应力强度因子KⅠ值及J积分值，结果见表1所列。

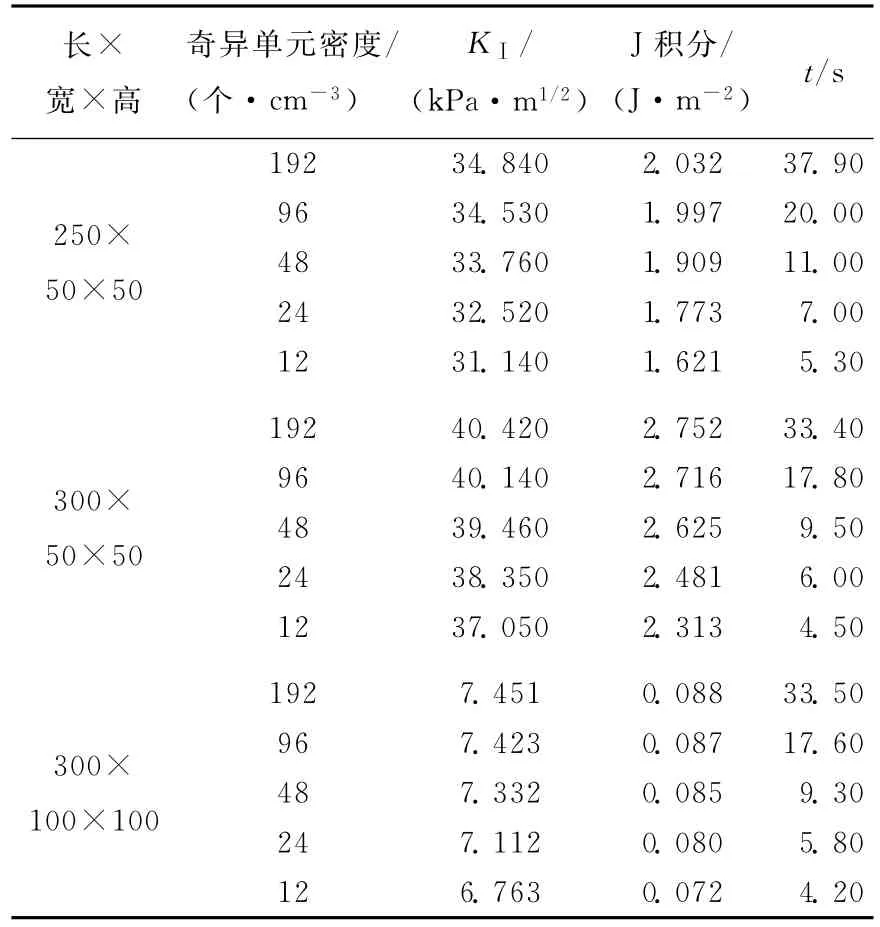
表1 不同网格密度下的KⅠ值及J积分值计算结果

2 网格密度对仿真结果的影响分析

通过表1中数据可得出如下规律：应力强度因子KⅠ值及J积分值均与网格密度值成正相关变化，但随网格密度的增加逐渐趋于平稳；计算时间与网格密度值成负相关变化，且无收敛趋势。随着网格的不断细化，计算结果逐渐趋向于准确解，但计算时间却明显增长。以尺寸为250 mm×50 mm×50 mm的模型为例，当细化部分奇异单元密度达到96个／cm3时，应力强度因子KⅠ值以及J积分值变化都已接近平稳，如图4所示。

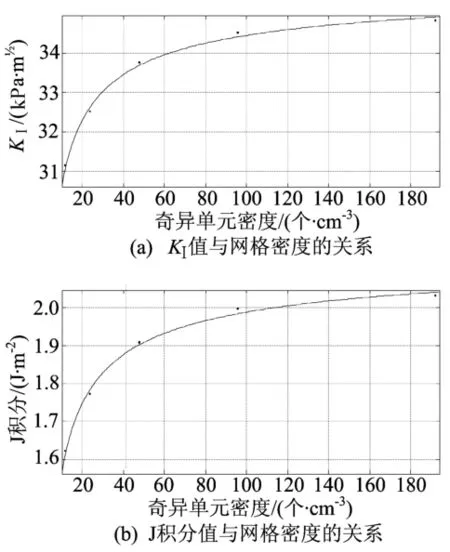
图4 250 mm×50 mm×50 mm尺寸模型计算结果随网格数的变化趋势

如果将细化区网格密度再增加1倍，即奇异单元密度为192个／cm3，与前者相比，KⅠ值变化了0.89%，J积分变化了1.76%，而计算成本却增加了89.5%。

从图4可以看出，当奇异单元密度较小时，计算值变化较大，难以满足精度要求，随着单元网格密度的增大，计算数据逐渐稳定。以奇异单元网格密度为自变量x，分别以KⅠ值及J积分值为因变量y，对图4中的各曲线进行拟合。为了使拟合系数R2更接近1，结合图4中的曲线变化趋势，最终确定采用y＝axb＋c形式的拟合函数，其中，y为计算值；x为网格密度；a、b、c均为拟合系数。

3种尺寸（尺寸1，250 mm×50 mm× 50 mm；尺寸2，300 mm×50 mm×50 mm；尺寸3，300 mm×100 mm×100 mm）下的KⅠ拟合方程分别如下：

尺寸1，y＝－19.04x－0.5463＋36；

尺寸2，y＝－18.21x－0.5726＋41.37；

尺寸3，y＝－8.315x－0.9668＋7.515。

3种尺寸下的J积分拟合方程分别如下：

尺寸1，y＝－2.048x－0.5274＋2.169；

尺寸2，y＝－2.342x－0.5687＋2.879；

尺寸3，y＝－0.185 6x－0.9521＋0.089 13。

取x趋向正无穷大时的极限值为稳定值，结果见表2和表3所列。

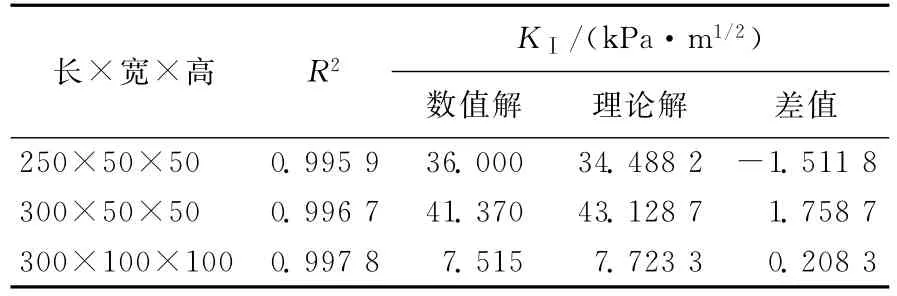
表2 KⅠ值曲线拟合结果与理论解对比

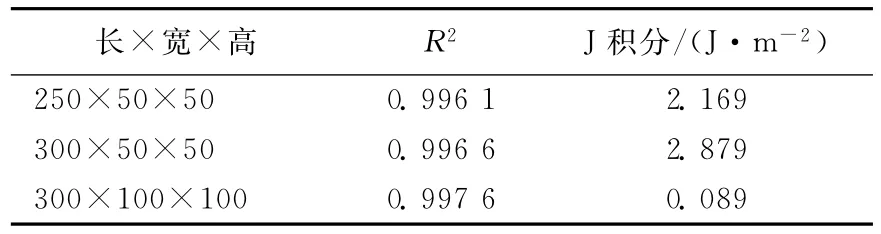
表3 J积分值曲线拟合结果

3组小梁试样的数据输出点距小梁底面距离均为0.45 mm，由经验公式［18］计算得到在8.4 k N荷载作用下，各试件在数据输出点处的应力强度因子KⅠ值的理论值见表2所列，从表2中可以看出，由经验公式得出的理论解与有限元软件得出的数值解相一致，由此可以看出利用有限元软件得到的计算结果是可靠的。

以数值解的稳定值为准确解，取5%为可接受的最大误差，通过曲线方程，可以反算出各计算结果为稳定值的95%时所对应的奇异单元密度，即为合理网格密度，见表4所列。

由于模型宽度方向每层网格单元尺寸为0.5 cm，奇异单元区截面积为2 cm2，故每层奇异单元的体积为1 cm3，另外奇异单元自虚拟裂缝向外共有3个围道，每一层围道的第1围道内的奇异单元数为虚拟裂缝周围的奇异单元数，故虚拟裂缝周围的合理单元数即为合理奇异单元密度的1／3，由此得出不同尺寸模型所对应的虚拟裂缝周围合理单元数见表4所列。

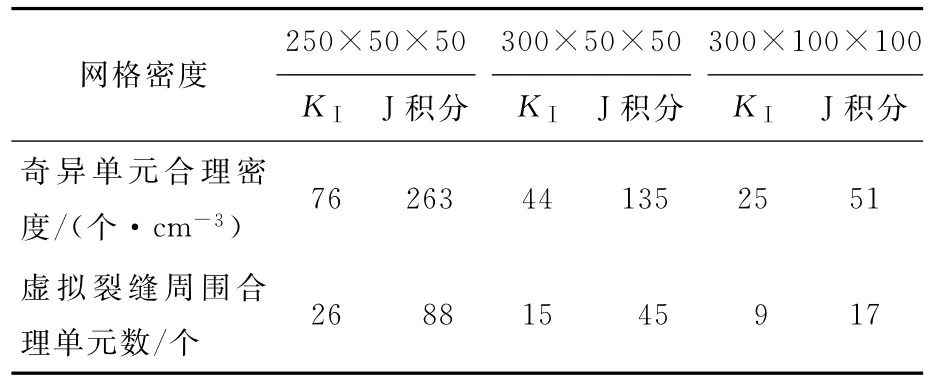
表4 不同尺寸模型的合理网格密度

3 基于Matlab GUI的数据库开发

将得到的不同尺寸模型的合理单元尺寸基于Matlab GUI开发一套交互界面的数据查询系统。系统的主界面如图5所示。

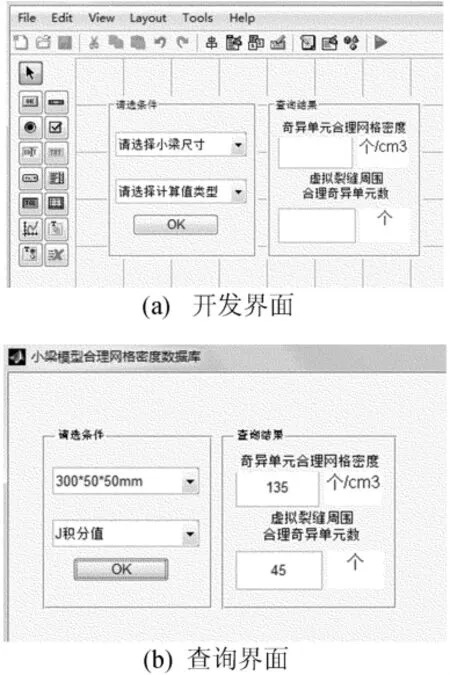
图5 数据库主界面

系统由2块主面板组成，一个为条件选择面板，另一个为查询及结果输出面板。以模型尺寸以及所要模拟计算的数据类型为输入条件，以奇异单元的合理密度以及虚拟裂缝周围的合理单元数为输出结果，单击“OK”按钮，即可抽取数据库中满足查询条件的结果值。例如在模型尺寸下拉菜单中选择“300 mm×50 mm×50 mm”，在计算值类型下拉菜单中选择“J积分值”，单击“OK”按钮，得到的查询结果为：“奇异单元合理网格密度为135个／cm3”、“虚拟裂缝周围合理奇异单元个数为45个”，如图5b所示。

4 结 论

（1）对网格密度值和计算结果值进行函数拟合，以网格密度趋于无穷时该函数的极限值为精确值。分析表明，达到该精确值95%时的网格密度可平衡计算结果精度和计算成本。

（2）对于沥青混合料小梁弯曲试验，不同尺寸模型依据KⅠ值和J积分值确定的合理网格密度也不相同。

（3）通过Matlab GUI对计算结果建立交互界面查询系统，能直接给出不同尺寸模型依据KⅠ值和J积分值确定的合理网格密度。

［1］ 秦 昊，梁乃兴，陆兆峰.水－温作用下沥青混合料疲劳性能分析［J］.中南大学学报：自然科学版，2011，42（4）：1126－1132.

［2］ Xu Ouming，Han Sen，Gao Shijun，et al.Effect of asphalt content on fatigue limit for asphalt mixture［J］.Journal of Traffic and Transportation Engineering，2009，9（6）：1－6.

［3］ 瞿 鑫，田小革，栾利强，等.沥青混合料疲劳寿命及其影响因素研究［J］.中外公路，2010，30（5）：266－269.

［4］ 茹忠亮，朱传锐，张友良，等.断裂问题的扩展有限元法研究［J］.岩土力学，2011，32（7）：2171－2176.

［5］ 罗 辉，朱宏平，陈传尧.预切口沥青混合料小梁疲劳试验与数值研究［J］.土木工程学报，2009，42（6）：126－132.

［6］ 周志刚，张清平，袁秀湘.沥青混凝土弯曲疲劳试验疲劳损伤分析［J］.中南大学学报：自然科学版，2011，42（6）：1743－1750.

［7］ Kim Y R，Baek C，Underwood B S，et al.Application of viscoelastic continuum damage model based finite element analysis to predict the fatigue performance of asphalt pavements［J］.KSCE Journal of Civil Engineering，2008，12（2）：109－120.

［8］ 蒋育红，黄晓明，廖公云.级配碎石夹层路面结构的断裂力学分析［J］.合肥工业大学学报：自然科学版，2009，32（4）：511－514.

［9］ 张少雄，王利永，孔 泉.网格粗细对于有限元模态分析计算的影响［J］.武汉理工大学学报，2006，28（5）：92－94.

［10］ 詹永祥，姚海林，卢正.表面含裂缝沥青路面低温收缩断裂分析［J］.交通科学与工程，2010，26（3）：20－24.

［11］ 罗 辉，朱宏平，陈传尧，等.基于FE／EFG耦合方法的沥青路面裂纹扩展模拟［J］.固体力学学报，2009，30（3）：292－300.

［12 李文成，郑 斌，张青军，等.沥青路面多裂纹温度应力的数值模拟［J］.华中科技大学学报：城市科学版，2010，27（3）：16－20.

［13］ Kuai H，Lee H J，Zi G，et al.Application of generalized J－integral to crack propagation modeling of asphalt concrete under repeated loading［J］.Transportation Research Record，2009，2127：72－81.

［14］ 刘敬辉，王端宜，刘 宇.采用J积分对沥青混合料抗裂性能进行评价［J］.固体力学学报，2010，31（1）：16－21.

［15］ Gross D，Seelig T.Fracture mechanics with an introduction to micromechanics［M］.New York：Springer Press，2006：59－134.

［16］ 石亦平，周玉蓉.ABAQUS有限元分析实例详解［M］.北京：机械工业出版社，2006：9－63.

［17］ Seweryn A.Modeling of singular stress fields using finite element method［J］.International Journal of Solids and Structures，2002，39（18）：4787－4804.

［18］ 王小召.水泥稳定碎石基层断裂性能的试验研究［J］.铁道建筑，2008，14（7）：117－120.