决策树模型在气管插管困难预测中的应用

重庆医科大学附属儿童医院(40003) 张 姝 张 强

现代临床麻醉实践中，气管插管困难是常见的呼吸相关的有害结果，在临床实际工作中，气管插管困难发生率大约是3% ～18%〔1，2〕，因严重的气管插管困难处理失败导致的死亡约占麻醉事故相关死亡病例30%〔3〕，且困难程度越高，脑损害或死亡的危险性越大〔4〕。因此，如果医生能事前预测困难气道插管难度并做好充分的心理和设备准备，可在一定程度上有效的防止困难气道插管的有害结果及降低死亡率。

目前大多是应用单一临床指标进行气管插管困难的预测，这些单指标预测的方法均存在一定缺陷，很多临床报道认为单指标预测结果并不可靠，假阳性和假阴性率较高〔5〕。近年来，国外有作者对气管插管困难的临床及解剖相关因素以及应用多项指标预测气管插管困难进行了探讨，但是尚没有建立适当的多指标综合统计模型对气管插管困难进行预测的报道。另外，目前临床上较为常用的预测方法其标准多是根据对外国人测量的结果制定的，这些预测方法的分类标准是否同样适用于中国人群也尚待研究。

资料来源

测量指标的确定由查阅相关专业文献、通过麻醉专业专家讨论之后，选取专业上认为能够反映可能造成气管插管困难的相关因素的指标，包括性别、年龄、身高、体重、改良的Mallampati口咽评级、上唇咬合实验评级、门齿间距、头后仰角度、颏甲间距、下颌骨角度、下颌骨长度、双下颌间距、颈围、颈长度14个指标，其中连续性变量11个，离散型变量3个。纳入对象为拟行气管插管择期手术的全麻住院病人，排除对象为凡有能确诊为患有可能造成困难气管插管的疾病的患者，如面部畸形、头颈部活动度受限、气道病理性改变等，从而排除了某些疾病对气管插管难度分级的影响。纳入病人共计826例。

方 法

随着计算机技术的发展，基于决策树的分类方法是数据挖掘中较为典型的分类预测的方法，一棵决策树的内部节点是属性或者属性的集合，叶节点是所要划分的类，它采用自顶向下(Top-Down)的递归方式，在决策树的内部节点(internal node)进行属性的比较，并根据不同属性判断从该节点向下的分支，在决策树的叶节点得到结论〔6－7〕。

CART(classification and regression tree)算法又称BFOS算法，在1984年由美国加利福尼亚大学的 Leo Breiman和斯坦福大学的 Jerome H．Friedman提出，其应变量主要是二值分类变量，也可以是多分类、有序变量及连续型变量，自变量可以是离散变量，也可以是连续型变量。构造CART决策树的思路为:在整体样本数据的基础上，生成一个层次多，叶节点多的大树，以充分反映数据之间的联系，然后对其进行删减，产生一系列子树，从中选择适当大小的树，用于对数据进行分类。假设样本空间T包含为两类样本A类、B类，CART算法按照一定的规则对其进行分割，产生两个节点，即子集 T1、T2，满足 T=T1∪T2且 T1∩T2= Ø，这个过程重复进行，直到按照某种标准，节点无法再分，成为最终的叶节点。

CART决策树生成的具体过程如下:

1.首先，认为CART的评估值为样本空间的常数，即为响应变量(response variables)的平均值。当响应变量的观测值发生变化时，CART的评估值可表示为:

其中，T是指样本空间，IT(x)是T的指标函数。

2.将样本空间分成两部分，选一个特定的变量Xj。如果Xj为一连续随机变量，选择一个指标量a，并

且定义:

5.继续对T1、T2按以上步骤进行分割，直到观测样本数变得很少或者样本冗余的平方和最小、所有叶节点的样本数为1或者样本属于同一类、决策树高度达到用户设置的阈值或者无属性变量可以用来进行分支时停止建树。

结果与分析

1．单指标改良的Mallampati口咽评分法(M法)预测结果

用Mallampati口咽评分法预测气管插管结果，两者都为困难或者都为不困难的共573人，预测结果与实际结果不同的共253人，即预测气管插管困难的总正确率为69.4%，其中，气管插管不困难者预测的正确率为79.7%，气管插管困难者预测的正确率为38.3%(表1)。

表1 气管插管患者Mallampati口咽评级法预测结果

2．决策树模型CART算法预测结果

模型设置:根据本研究样本量情况，设定树结构最大层数为5，Gini系数的最小变化值须大于0.01〔8〕。CART算法采用最小代价－复杂度(cost-complexity pruning)修剪方法，该参数设定越大则得到的子树结构越简单，结合挖掘数据信息需要、预测准确率及树结构的简化程度，最终将复杂度参数设为0.5。在交叉验证数据集拆分项中，考虑到样本量不是很大的情况，选择20次拆分的方法，即每次随机选取95%的数据作为训练集，剩余5%的数据作为测试集，保证每个数据仅有一次进入测试集〔9〕。

本研究建立的决策树模型以所有数据为根节点，以头后仰度差为第一分层变量，树高共6层10个叶节点(图1)。图中每个节点矩形框中标示了该节点包含的总人数、气管插管容易及困难分别对应的人数及构成比，每个节点处以构成比高的结果属性标记为该节点的类别，并以亮色长条表示。根据该决策树可以看到，最后进入模型的变量有7个，分别为头后仰度差、年龄、颈围、性别、门齿间距、双下颌间距和下颌骨角度，可以提取以下分类规则:

规则1:头后仰度差≤13.5cm+年龄＞54岁;

规则2:头后仰度差≤13.5cm+年龄≤54岁+性别=男;

规则3:头后仰度差＞13.5cm+颈围＞39.25cm+年龄＞48岁;

规则4:头后仰度差＞13.5cm+颈围＞39.25cm+年龄≤48岁+双下颌角间距≤11.85cm;

规则5:头后仰度差＞13.5cm+33.95＜颈围≤39.25cm+下颌骨角度≤56.5°。

根据以上规则对气管插管进行分类预测，该模型分类的总正确率为82.1%，其中对气管插管不困难者分类的正确率为82.4%，气管插管困难者分类的正确率为81.1%。

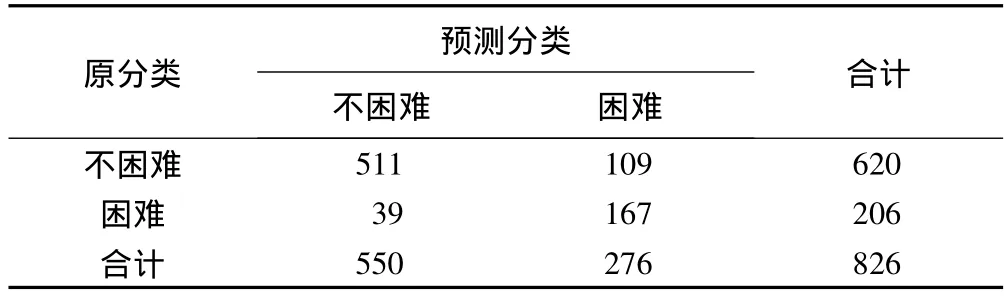
表2 气管插管患者CART算法模型分类结果

3．传统单指标预测结果与决策树模型预测结果比较

以传统的预测方法及决策树模型分类后每个个体所得的预测概率拟合ROC曲线，计算曲线下面积(图2)，采用单一指标进行预测的M口咽评级法曲线下面积为0.590，说明分类效能不高，其曲线下面积与0.5比较，差别有统计学意义(P＜0.001)，可以认为该方法所进行的分类有效，但是效果不好;CART算法决策树模型曲线下面积为0.879，其曲线下面积与0.5相比，差别有统计学意义(P＜0.001)，分类效果较好(表3)。

讨 论

本研究建立的CART算法决策树模型是既可以处理连续性变量又可以处理离散型变量的分类模型。决策树模型的优点在于树的构建过程不受变量间共线性的影响，并且可以提示变量间可能存在的交互作用，从而使模型输出结果更易于解释。由于本研究中没有数据缺失值的情况存在，未能体现决策树模型在数据存在缺失值的情况下使用的优势所在。传统的统计模型一般自身不能进行缺失值的有效处理，而缺失值是实践中普遍存在的问题〔10－12〕，传统方法只能删除缺失数据或者采用一定的方法先对数据进行填补，而决策树本身可以把缺失值的属性当作独立于其他属性值的类参与决策树的构建，而且可以利用其算法并经过一定的修正有效处理缺失数据。

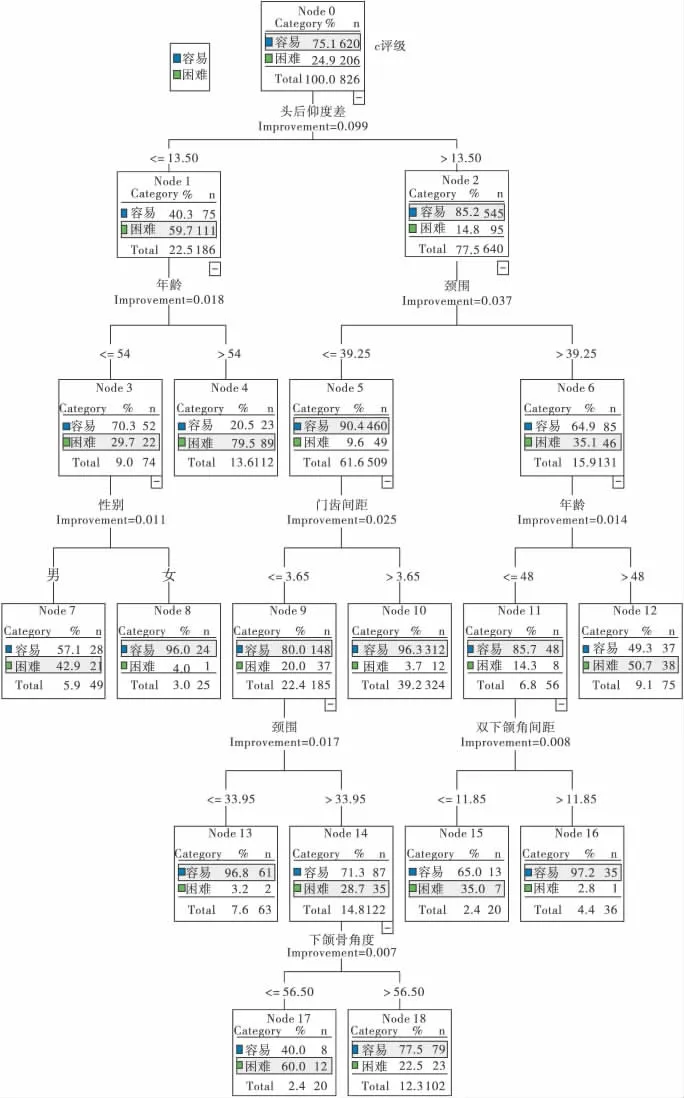
图1 气管插管困难CART算法决策树结构图

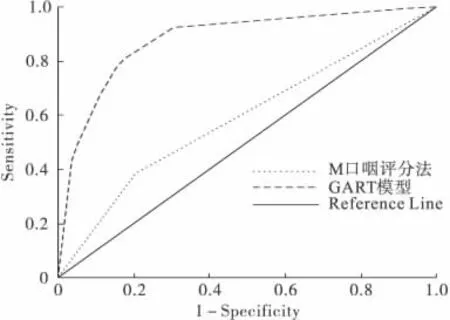
图2 单指标预测与CART模型预测roc曲线比较

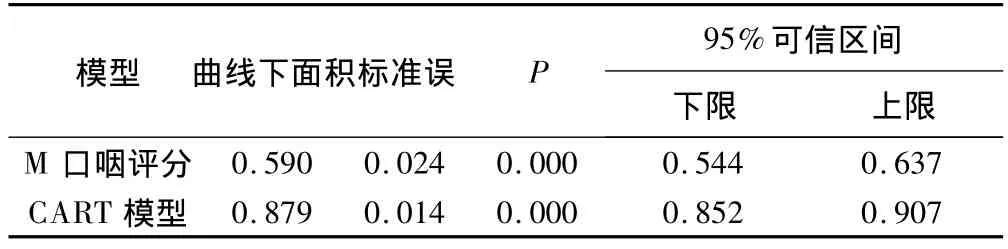
表3 气管插管困难两种预测方法ROC曲线下面积

从模型结果来看，用目前临床上常用的单指标预测方法Mallampati口咽评分法对气管插管困难进行了预测，本研究显示虽然这种方法预测快速、方便，但是预测的准确率仅为69.4%，特别是对临床上非常重要的气管插管困难者的预测准确率更低，仅为38.3%，对于大部分患者无法进行正确的预测。决策树模型预测的准确率为82.1%，预测效果较为理想。

从模型结果的表达方式及易用性来看，决策树模型最后采用逻辑“是”、“非”的表达方式，结果更加直观，不需进行任何数学计算，在临床使用方便。另外，从决策树模型最终的输出结果还可以看到，对于连续性变量，模型都给出了该变量用于分类时的最佳分割点，从而可以直观的看到某个因素对最终结果影响的分界点。

总之，综合运用多指标建立的气管插管困难预测模型比单指标预测方法预测效果更好，CART算法的主要优点在于剪枝过程中采用了交叉验证(cross validation)的方法来寻找最优树，解决了在小样本集上决策树由于没有独立测试样本集而造成的过度拟合问题，这样形成的全局决策树在性能上非常近似于由包含所有样本的原始训练样本集得出的决策树。与神经网络模型相比，决策树分类结果更简单、明确，结构直观，能清楚显示对分类或预测有意义的变量，更容易理解;与传统统计方法相比，决策树预测结果更简单、明了，并且能够处理有缺失值的数据以及变量间的共线性问题，有利于充分利用资料信息，得到分类预测准确率更高，结果更直观的预测模型。

1．薛富善主编．困难气管插管技术．科学技术文献出版社，2002．

2．Crosby ET，Cooper RM，Douglas MJ，et al．The unanticipated difficult airway with recommendations for management．Can J Anaesth，1998，45:757-776．

3．Andropoulos DB，Rowe RW，Betts JM．Anaesthetic and surgical airway management during tracheo-oesophageal fistula repair．Paediatric Anaesthesia［Paediatr Anaesth］，1998．

4．王世泉编著．麻醉与抢救中气管插管学．人民军医出版社，2005．

5．Toshiya shiga，Zen'lchiro Wajiama，Tetsuo Inoue，et al．Predicting difficult intubation in apparently normal patients:a meta-analysis of bedside screening test performance．Anesthesiology，2005，103:429-437．

6．史忠植主编．知识发现．清华大学出版社，2002．

7．Peter Waiganjo Wagacha．Induction of Decision Trees．Foundations of Learning and Adaptive Systems，2003．

8．Stalans LJ，Yarnold PR，Seng M，et al．Identifying three types of violent offenders and predicting violent recidivism while on probation:a classification tree analysis．Law ＆ Human Behavior，2004，28(3):253-71．

9．孙微微，刘才兴，田绪红．训练集容量对决策树分类错误率影响的研究．计算机工程与应用，2005，10:159-161．

10．Arnold Alice M，Kronmal Richard A．Multiple imputation of baseline data in the cardiovascular health study．American Journal of Epidemiology，2003，157(1):74-84．

11．曹阳，张罗漫．运用SAS对不完整数据集进行多重填补--SAS9中的多重填补及其统计分析过程(一)．中国卫生统计，2004，21(1):56-63．

12．Abraham，W Todd，Russell，et al．Missing data:a review of current methods and applications in epidemiology research．Current Options in Psychiatry，2004，17(4):315-321．