复发事件资料的生存分析在临床试验中的应用及SAS实现
2012-03-11上海交通大学医学院生物统计学教研室200025张莉娜
上海交通大学医学院生物统计学教研室(200025) 张莉娜
有些事件可能在一个受试者身上多次发生。每两次连续事件之间的时间间隔称为等待时间。这类资料称为复发事件资料(recurrent event data)。其特点是上次事件的发生对下次事件发生的迟早有很大影响,即对一名受试者来说,各次事件之间是相关的。
本文应用临床试验中一个实例分别用总时间模型(total time model)和边际模型(marginal model)进行复发事件资料的生存分析,并用稳健的夹心方差估计方法对模型的回归系数进行估计,并给出PHREG的过程实现。
资 料
为了评价某新药治疗成人慢性乙型肝炎的有效性,采用多中心、随机、双盲双模拟、阳性药物平行对照的Ⅱ期临床试验,对238例受试者的HBV DNA进行重复观测。以HBV DNA阴转作为终点事件(HBV DNA≤103),记录各次HBV DNA阴转的时间。所有符合试验方案、依从性良好、试验期间未服用禁止用药、完成CRF的病例纳入PP(Per protocol)分析集,由于无效而提前退出的病例也纳入PP分析,共218例受试者进入PP分析集。
分别在治疗前、治疗4周、治疗12周、、治疗24周、治疗36周、治疗48周、治疗52周各个时间点记录每个受试者的HBV DNA,见表1。

表1 两组慢性乙型肝炎患者各个时间点的HBV DNA情况
方 法
1.总时间模型
它把整个随访时间按终点事件的发生分为数个时间段,并考虑了终点事件发生的先后顺序。一个受试者只有在发生前一次事件后才能进入下一个危险集,即受试者在k-1个事件发生后,才处于发生第k个事件的风险中,分层变量采用顺序号赋值是为了保证这种事件发生的先后顺序。所以此模型属于条件模型(conditional model)。第k次事件的风险函数为:

其中 β1,β2,…,βp为第 k次终点事件的 p 个变量的回归系数;x1k,x2k,…,xpk为发生第k次终点事件的p个变量的取值;h0k(t)表示t时刻发生第k次终点事件的基线风险;hk(t,xk)表示在第t时刻经历第k次终点事件的风险。此模型由Prentice,Williams和Peterson提出,故又称为PWP模型。
总时间模型的数据格式整理如表2形式,放在数据集pwp中。
其中loghbv0为治疗前HBV DNA的对数值,分层变量enum为阴转事件序列号,etstart和etstop分别为每次阴转事件开始观察的时间和阴转事件结束观察的时间,status=1表示阴转事件发生,status=0表示阴转事件未发生。

表2 总时间模型数据格式
2.边际模型
所有受试者,不论个体实际发生了多少次事件,都被包括在所有事件的危险集中,对每次事件都是从随访开始计时。对每一受试者,无论他实际发生了多少次终点事件,但在分层赋值中仍有6个值,此值即为随访次数,6是发生终点事件的最大可能次数。这一模型是在配合Cox分层模型的过程中加入了一个类似GEE算法的稳健协方差矩阵。此矩阵的结构是:
Cov(^β)=V(β)[L'L]V(β)
式中V(β)是关于β的信息矩阵的逆组成的P×P维矩阵,L是n×p维的记分残差矩阵。此模型由Wei,Lin和Weissfeld提出,故又称为WLW模型。
边际模型的数据格式整理如表3形式,放在数据集wlw中。

表3 边际模型数据格式
其中loghbv0为治疗前HBV DNA的对数值,分层变量visit=i表示第i次随访,vtstop为每次随访结束观察的时间,status=1表示阴转事件发生,status=0表示阴转事件未发生。
3.夹心方差估计(sandwich variance estimator)
Lin和Wei提出用最大似然法或偏最大似然法估计回归系数的参数,并根据个体内的相关性校正方差的估计值(夹心方差估计值),使标准误的大小更接近实际情况,是一个稳健的估计方法。
用SAS9.1中的PHREG过程分别以总时间模型和边际模型来实现复发事件资料的生存分析。
SAS程序如下:
title‘PWP total time model with common regression coefficients’;
proc phreg data=pwp covs(aggregate);model(etstart,etstop)*Status(0)=group loghbv0;id no;strata enum;
run;
title‘PWPtotal time model with stratum-specific regression coefficients’;
proc phreg data=pwp covs(aggregate);
model(etstart,etstop)*Status(0)=g1 g2 g3 g4 g5 g6 x1 x2 x3 x4 x5 x6;
strata Enum;
g1=group*(Enum=1);x1=loghbv0*(Enum=1);
g2=group*(Enum=2);x2=loghbv0*(Enum=2);
g3=group*(Enum=3);x3=loghbv0*(Enum=3);
g4=group*(Enum=4);x4=loghbv0*(Enum=4);
g5=group*(Enum=5);x5=loghbv0*(Enum=5);
g6=group*(Enum=6);x6=loghbv0*(Enum=6);
run;
title‘Wei-Lin-Weissfeld Model’;
proc phreg data=wlw covs(aggregate);
model vtstop*Status(0)=gg1 gg2 gg3 gg4 gg5 gg6 xx1 xx2 xx3 xx4 xx5 xx6;
gg1=group*(visit=1);xx1=loghbv0*(visit=1);
gg2=group*(visit=2);xx2=loghbv0*(visit=2);
gg3=group*(visit=3);xx3=loghbv0*(visit=3);
gg4=group*(visit=4);xx4=loghbv0*(visit=4);
gg5=group*(visit=5);xx5=loghbv0*(visit=5);
gg6=group*(visit=6);xx6=loghbv0*(visit=6);
strata visit;
id no;
run;
程序解释:先用总时间模型对复发事件生存资料进行分析,分别估计各变量的公共回归系数和各变量在各分层的回归系数,HBV DNA阴转事件序列号enum为分层变量。
经历 k(k=1,2,3,4,5,6)次阴转事件的比例风险函数模型可以写为:
H(t,g1,g2,g3,g4,g5,g6,x1,x2,x3,x4,x5,x6)=h0k(t)exp(β11g1+β12g2+ β13g3+ β14g4+ β15g5+ β16g6+ β21x1+β22x2+ β23x3+ β24x4+ β25x5+ β26x6) (k=1,2,3,4,5,6)
再用边际模型对复发事件生存资料进行分析,估计各变量在各分层的回归系数,随访次数visit为分层变量。
第 k(k=1,2,3,4,5,6)次随访发生阴转事件的比例风险模型可以写为:
H(t,gg1,gg2,gg3,gg4,gg5,gg6,xx1,xx2,xx3,xx4,xx5,xx6)=h0k(t)exxp(β11gg1+ β12gg2+ β13gg3+β14gg4+ β15gg5+ β16gg6+ β21xx1+ β22xx2+ β23xx3+ β24xx4+ β25xx5+ β26xx6)(k=1,2,3,4,5,6)
对于每一个考虑纳入模型的协变量需用k个指示变量表示,分别对应于k个时间段。
选项covs(aggregate)表示选用夹心方差估计方法。
结 果
试验药(group=2)与对照药(group=1)出现HBV DNA阴转的风险比为HR=1.184,P=0.056,即服用试验药比服用对照药,HBV DNA的阴转风险更大,阴转时间更短,试验药优于对照药。治疗前HBV DNA的对数值每增加一个单位,出现HBV DNA阴转的风险比为HR=0.848,P<0.0001,即治疗前的HBV DNA值越大,阴转风险越小,阴转时间越长。

表4 总时间模型的公共参数估计及假设检验
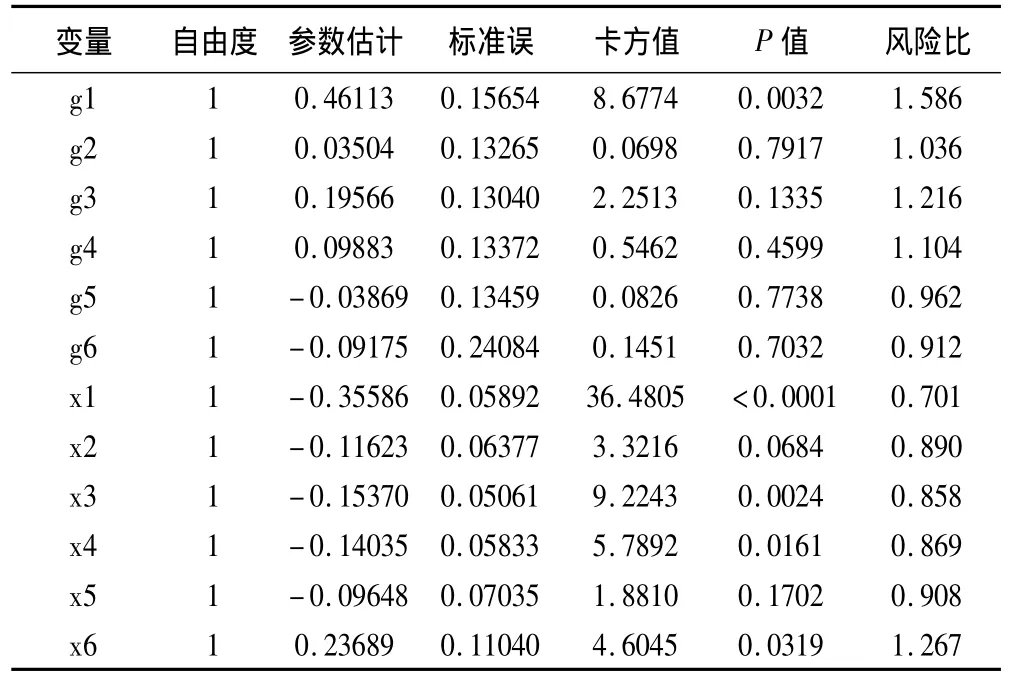
表5 总时间模型的分层参数估计及假设检验
g1,g2,g3,g4 的风险比 HR >1,g5,g6 的风险比HR<1,说明经历1~4次阴转,服用试验药比服用对照药,HBV DNA的阴转时间更短;而对于经历5和6次阴转这两个终点事件,服用试验药比服用对照药,HBV DNA的阴转时间更长。从检验水平分析,只有g1具有统计学意义。
由x1~x6的风险比可知,对于前5次HBV DNA阴转事件,治疗前的HBV DNA越大,阴转风险越小,阴转时间越长,且随着阴转次数的增加,风险比HR越来越接近1。而对于第6次阴转事件来说治疗前的HBV DNA越大,阴转风险越大,即对于治疗前HBV DNA值越大的受试者,在经历了前5次阴转事件后,最后一次阴转的可能性也越大。
由gg1~gg6的风险比都大于1可知,对于每一次随访,每一个时间段,服用试验药后HBV DNA阴转的风险都大于服用对照药,且随着随访时间的增加,风险比HR越来越小,直至接近于1,即随着随访时间的增加,试验药和对照药对于HBV DNA阴转风险的影响越来越接近。而从检验水平分析,前三次随访的P值接近0.05,说明服药后的前期(24周内)试验组比对照组HBV DNA阴转的风险大。
由xx1~xx6的风险比都小于1可知,对于每一次随访,治疗前的HBV DNA越大,在该随访时间段的阴转风险越小,且随着随访时间的增加,风险比HR越来越大,直至接近1,即随着时间的增加,治疗前HBV DNA值的大小对阴转风险的影响越来越小。
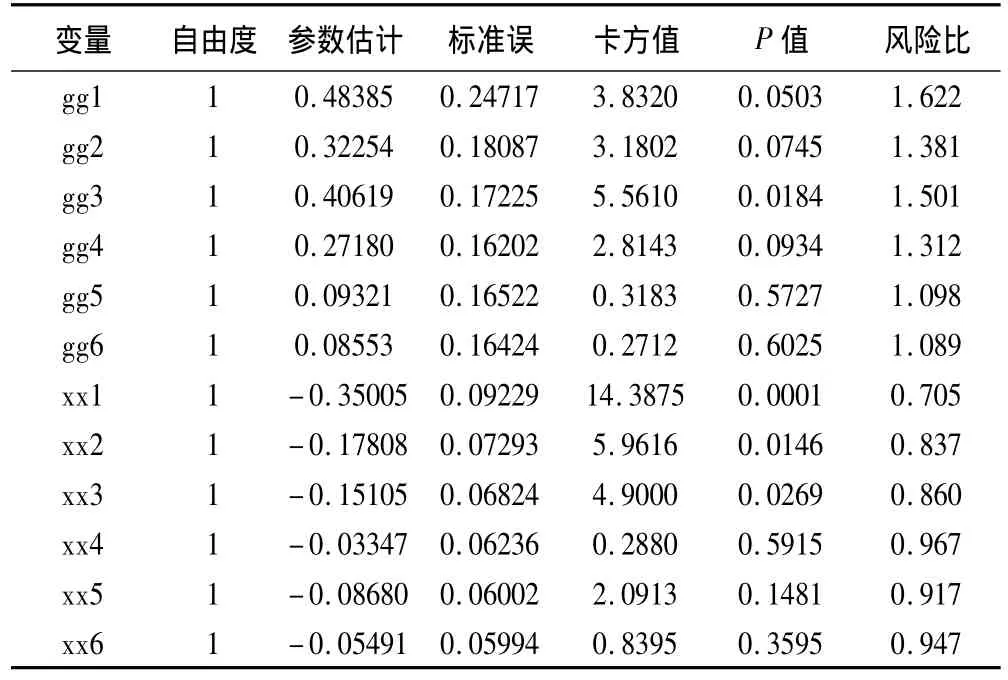
表6 边际模型的分层参数估计及假设检验
讨 论
本文中应用的总时间模型和边际模型都可用来处理复发事件的生存时间资料,所不同的是生存时间的定义以及对数据结构方面的要求不同;并且通过定义协变量在各次复发事件对应不同的取值,实现同一协变量对应各次复发事件的风险比HR不同,以更符合实际情况。
1.Hosmer DW,Lemeshow S.Applied survival analysis:regression modeling of time to event data.John Wiley & Sons,lnc.New Yark,1999:308-316.
2.Shoukri MM,Pause CA.Statistical methods for health sciences.Second Edition.CRC Press LLC,1999:369-375.
3.Kleinbaum DG,Klein M.Survival analysis:a self learning text.Second Edition.Springer Science+Business Media,lnc,2005:331-390.
4.Allison PD.Survival analysis using SAS:a practical guide.Second Edition.Cary,NC,USA:SAS Institute Inc,2010:260-281.
5.苏霞,钱国华,荀鹏程,等.临床试验中多维生存时间资料的分析.中国临床药理学与治疗学,2006,11(9):1073-1077.
6.余松林,向惠云,编著.重复测量资料分析方法与SAS程序.北京:科学出版社,2004,3.
7.高惠璇,等编译.SAS系统SAS/STAT软件使用手册.北京:中国统计出版社,1995,4.
