排队论G/Ek/c模型及其在医院眼科专家门诊中的应用

章顺悦 杨 扬 吴家利 宋婷婷 陈远方 刘文华 尹 平△

近年来，排队论模型在医疗服务领域中的应用受到了极大地关注〔1－2〕。由于医疗资源的相对短缺，一些大型综合性医院的排队拥挤现象普遍存在。但病人到达医疗机构的间隔时间分布往往又不可控，例如交通状况，天气、季节因素，病人流量和坐诊医生的口碑，以及目前兴起的预约排队与窗口排队结合等都可能影响病人的到达，难以用确切的概率分布函数来表达。而排队论G/Ek/c模型则可较好的解决此类复杂问题。本文通过介绍排队论G/Ek/c模型的原理与参数估计，并对武汉市某大型综合性医院的眼科专家门诊就诊患者的排队数据进行拟合，以期为优化医院眼科专家门诊的人力资源配置，缩短病人的排队等候时间提供科学的决策依据。

G/Ek/c模型的基本结构

G/Ek/c模型指顾客的到达规律服从一般分布(G)，服务时间服从爱尔朗分布(Ek)，有c个服务台的排队论模型。其对顾客的到达时间分布没有特定限制，适用范围广泛。以医院眼科专家门诊为例，介绍该模型的结构。

1.顾客源

顾客源是指接受服务的对象。医院眼科专家门诊就诊的病人即为顾客源，假设其为无限。病人到门诊的分布受到很多因素影响，其间隔时间可认为服从一般分布(G)。

2.队列

在得到服务前等待的病人组成队列，以其能容纳的最大顾客数量为标志。医院的队列多由若干个队长组成(如3名专家坐诊，则由3个队长组成队列)，而且患者挂号后通常不会因为排队的队伍太长而轻易离开，视为无限队长。

3.排队规则

排队规则指服务机构是否允许顾客排队，顾客对排队长度、时间的容忍程度以及在排队队列中等待服务的顺序。该专家门诊按照先到先服务(FCFS)的等待制排队规则，但中间插入了之前预约的患者，同时检查归来的患者与新到患者交叉接受诊治。

4.服务台与服务时间

专家门诊的医生可视为服务台。为单个顾客提供服务开始到服务结束为止的时间跨度为服务时间。在眼科专家门诊的诊疗过程中，病人的服务时间基本稳定，其经验分布大多近似爱尔朗分布。

资料来源

以武汉市某大型综合性医院的眼科专家门诊排队系统为研究对象。收集了2011年4月中旬两个星期，从周一到周五共10天该眼科专家门诊病人的到达情况。考虑到每天下午4点后专家门诊基本上都在处理之前排队的病人和预约病人，因此，每天的观察时间为早上8点到下午4点。以患者到达接诊台登记等待为标志，进入排队系统，结束服务离开为终止标志。共获得390位就诊患者的排队数据资料。

G/Ek/c模型拟合与参数估计

1.G/Ek/c模型拟合

在观测的10天共80小时期间，390位就诊患者的到达率为4.88(人/小时)。其中，到达的间隔时间最短为5分钟，最长20分钟，中位数为12.5分钟，算术平均数为10分钟。可将病人相继到达医院眼科专家门诊的间隔时间分布看作一般分布(G)。

对于病人服务时间的分布，介于等长分布(D)与负指数分布(M)之间，即服务时间的偏差介于0与1/μ之间〔3，4〕。用来拟合这类中间情况的理论服务时间分布为爱尔朗分布，具有较好的灵活性〔5〕。事实上，负指数分布和等长分布就是爱尔朗分布当k=1和k≈∞时的特例。

所谓爱尔朗分布，即设v1，v2，…，vk是k个相互独立的随机变量，服从相同参数kμ的负指数分布，令T=v1+v2+…+vk，则T的概率密度函数为

且t＞0，称T服从k阶爱尔朗分布〔6〕。公式中 k和μ均为正，且k为整数。它的平均值为1/μ，方差为(1/kμ)2。为此，对一个经验服务时间分布的平均值和方差进行估测后，利用平均值和方差的公式即可用于确定k的整数值，并使其与估测值非常接近〔7〕。

由收集的服务时间记录，取μ=1.5(人/小时)，k=2，拟合爱尔朗分布。结果表明该眼科专家门诊患者服务时间的分布服从k=2，均数为2/3(小时)，方差为1/9的2阶爱尔朗分布(χ2=3.1477，P=0.5334)，见表1。因此，可按病人依次到达间隔时间服从一般分布G，服务时间服从Ek分布进行 G/Ek/c模型拟合。

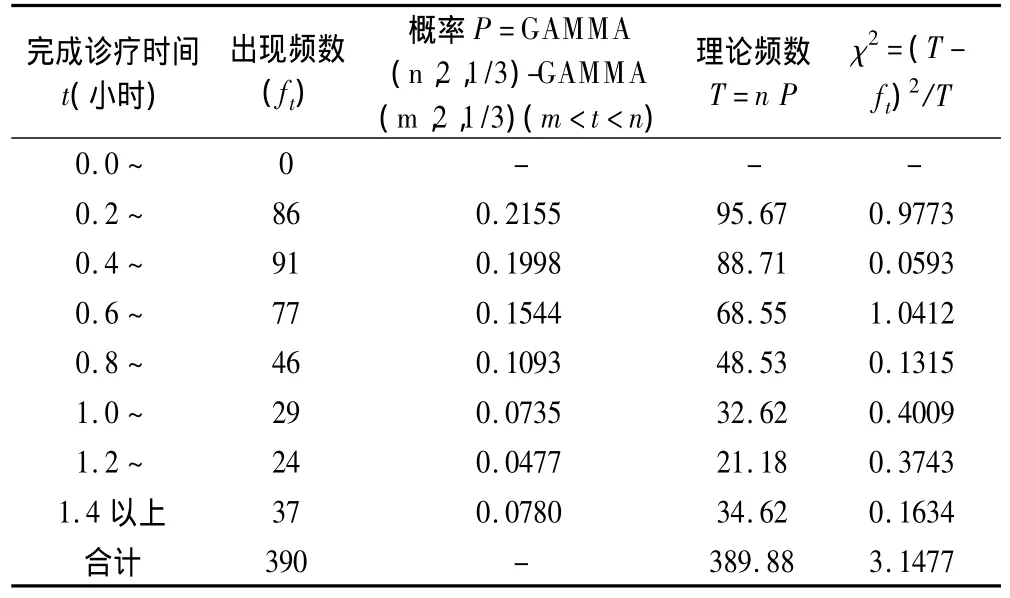
表1 眼科专家门诊服务时间的2阶爱尔朗分布拟合结果

2．G/Ek/c模型的参数

记排队系统整个服务机构的服务强度为ρ，是服务系统的平均利用率，即ρ=λ/cμ。当ρ＜1时，不会排成无限队列，系统平均到达率等于离去率，达到平衡状态。排队论模型的求解是基于平衡状态下的定量指标。主要指标如下〔10〕:

λ—系统中新顾客的平均到达率;

c—服务台数;

μ—整个系统的平均服务率;

ρ—服务强度，即服务设施的利用因子，是平均到达率与平均服务率之比;

ρ=λ/cμ;

P0—服务台空闲概率;

Pn—系统中有n个顾客的概率;

Ls—队列长，系统中的顾客总数;

Lq—排队长，队列中正在排队等待的顾客数;

Ws—逗留时间，顾客在系统中的停留时间，包括等待时间和服务时间;

Wq—等待时间，顾客在队列中的等待时间;

相关指标相互关系的Little公式:

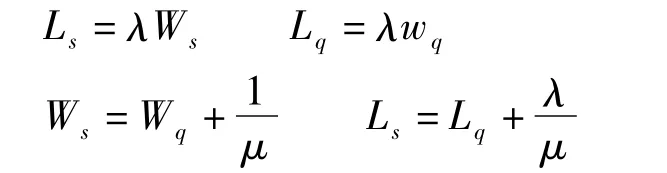
3．G/Ek/c模型参数估计

G/Ek/c模型的参数估计较复杂，国内尚无详细的文献介绍。目前，国外文献报道了几种不同的解法，主要采用近似的逼近法〔8－9〕，基本求解过程如下〔10〕。

设排队系统在稳定状态下，n为在时间x系统中的人数，l为在时间x到达的人数，i为系统中正在接受服务的人数，s为在服务的服务台数，在时间x有顾客n个的概率为P，则有

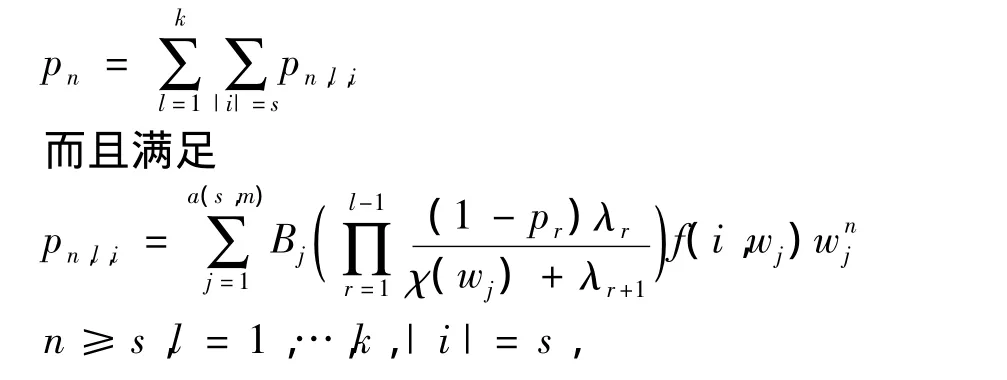
公式中a(s，m)为线性方程，wj是方程的根，且Bj和wj满足如下方程:

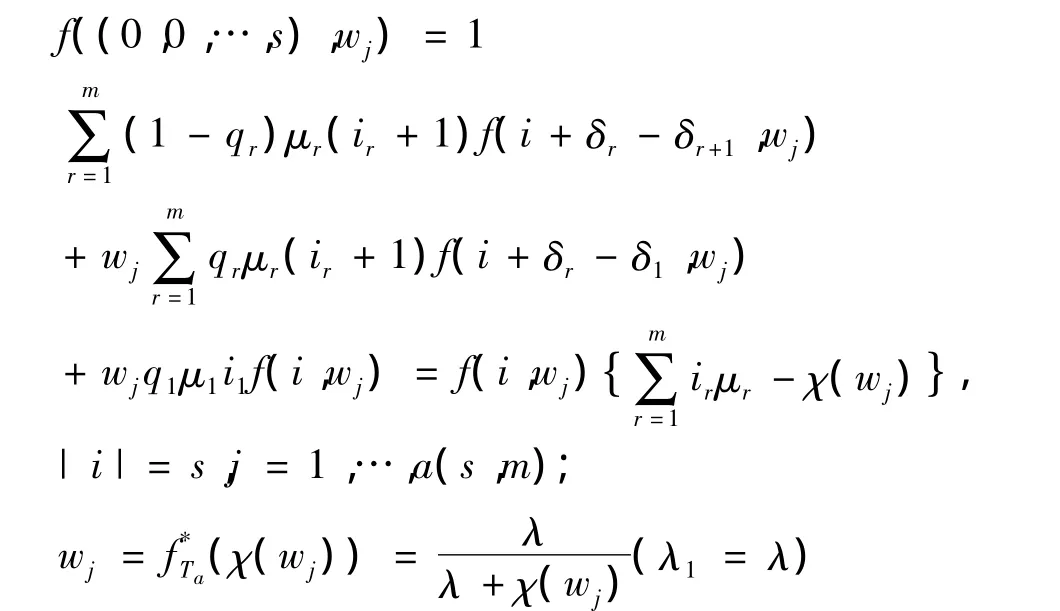
在采用FCFS规则下，假设新到顾客的平均等待时间为:

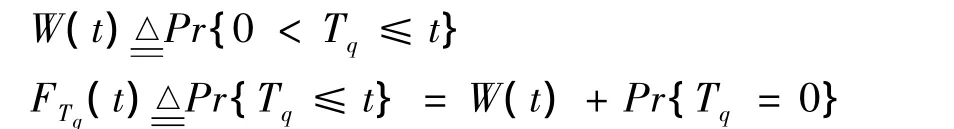
模型在稳定状态下，解以上方程，平均等待时间近似为

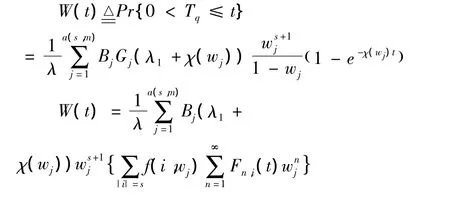
由解得的Lq和Wq，根据Little公式〔6〕，其它指标也就可以计算出来了。

结 果

基于 λ =4.88(人/小时)，μ =1.5(人/小时)，k=2，对该眼科门诊的坐诊专家人数c为3人、4人和5人时，应用 G/Ek/c模型，利用软件 Open Office加载QtsPlus4Calc〔3－4〕计算得各项主要评价指标，如表 2 所示。并以系统中的病人数为横坐标，相应的概率为纵坐标，在c=3，c=4时绘制概率图，如图1和图2所示。

表2 G/Ek/c模型应用的参数估计结果

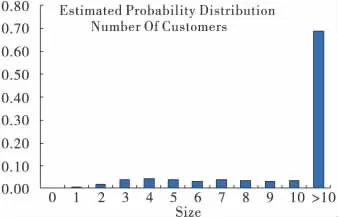
图1 c=3时系统中病人数的概率图

由以上结果可知，当有3位专家坐诊时，系统利用率为98.84%，平均每小时系统空置的概率为0.0013，队列中平均每小时19.96人，排队人数平均每小时16.99人，病人平均排队等待时间为3.54小时，且队列中大于10人的概率为0.6868。表明拥挤现象很严重。

如增加1位坐诊专家，即当c=4时，系统利用率为82.50%，平均每小时系统空置的概率为0.0040，队列中平均每小时4.14人，排队人数平均每小时不足1人，病人平均排队等待时间为0.17小时，且队列中有10人的概率降为0.0262。拥挤情况已经大为改善，效果相当明显，基本解决了拥挤排队的问题。

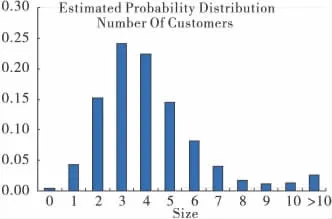
图2 c=4时系统中病人数的概率图

如增加2位坐诊专家，即当c=5时，系统利用率为66.71%，平均每小时系统空置的概率为0.0221，队列中平均每小时3.52人，排队人数平均每小时0.17人，病人平均排队等待时间为0.04小时，已经完全不存在排队拥挤的现象了。但相对4位专家的情况下，改善效果并没有明显增大，相对很高的人力成本来说，呈现出了浪费。

综合而言，该医院眼科专家门诊安排4位专家坐诊较为合理。

讨 论

到医院就诊排队是一种司空见惯的现象，我国由于医疗行业资源不够充分，这一现象显得更为突出。如果盲目增加服务窗口，包括配置人员或者相应的医疗设备，可能发生空闲和浪费。如果服务窗口配置不足，容易导致病人因排队时间太长而产生抱怨、不满、愤怒等负面情绪，甚至在排队过程中出现不良后果，对医院的满意度下降，直接影响病人对医院的选择和医院的品牌及整体管理质量。

本研究通过观察医院眼科专家门诊的排队状况，引入G/Ek/c排队论模型，对其人力资源配置进行评价和预测，为提高医院的服务效率，优化医疗资源配置提供了科学的参考依据。

1．王莹．排队论模型求解就医排队问题．科技资讯，2010，(17)．

2．Vasanawala SS，Desser T S．Accommodation of requests for emergency US and CT:applications of queueing theory to scheduling of urgent studies．．Radiology，2005，235(1):244-249．

3．周文正，尹平，马玉全，等．排队论模型M/D/c在医疗服务系统中的应用．中国卫生统计，2009，26(6):608-610．

4．周俊，周文正，尹平．G/M/c模型在医院口腔科门诊诊疗系统中的应用．中国医院统计，2010，17(2):135-138．

5．Rosenquist C J．Queueing analysis:a useful planning and management technique for radiology．．JMed Syst，1987，11(6):413-419．

6．Frederick S．hillier，Gerald J．Lieberman．运筹学导论．第八版．胡运权译．北京:清华大学出版社，2007，774-777．

7．Gorunescu F，Mcclean SI，Millard PH．Using a queueing model to help plan bed allocation in a department of geriatric medicine．Health Care Manag Sci，2002，5(4):307-312．

8．Avis D．Computing waiting times in GI/E ～ /s queueing system，TIMS Studies in Management Science，1977，7:215-232．

9．Ishikawa A．Stationary waiting time distribution in a GI/Ek/m queue，Oper．Res．Soc．Japan 27，1984:130-149．

10．Bertsimas D．An exact FCFSwaiting time analysis for a general class of G/G/s queueing systems．Queueing Systems 3，1988:305-320．