基于遗传算法收敛特性的停机准则＊

王 辉 徐晓英

（武汉理工大学理学院 武汉 430070）

0 引 言

作为一类模拟进化计算方法，遗传算法的基本框架、构成要素及操作策略已经形成，其搜索机理及收敛性理论也得到了深入的探索研究．目前，关于遗传算法的基础理论，较为完善的有Schema理论、遗传算法的马氏链分析及遗传算法的收敛理论［1］．

与收敛理论紧密相关的另一基本理论问题是遗传算法的收敛速度该如何表达．针对这一基本问题，文献［2］中Aytug和Koehlen利用马氏链中的首次访问时间概念，估计出遗传算法在一定的置信水平下访问到所有种群状态所需要的进化代数；文献［3］从转移矩阵的第二大特征值出发研究了标准遗传算法的停时准则；文献［4］中基于鞅理论研究了保留精英策略遗传算法的收敛速度，并给出了最大收敛代数的估算公式．

从目前多种估算方式和判断准则的研究中可以发现：（1）在判断遗传算法是否达到最优解时很少甚至并未考虑前代的信息，过于拘泥于概率意义上的计算；（2）在推导遗传算法最大收敛代数的估算公式中利用到全局最优解或最优解域的信息，而如何判断种群已达到最优解并未给出．

本文从遗传算法收敛性的定义出发，分析遗传算法的收敛特点，利用不同种群中最优个体适应值的一致性、种群的多样性分布，提出判断算法自动停止迭代的方法．为建立合适的停机准则及统一的遗传算法收敛速度度量方法提供参考．

1 遗传算法收敛定义及特点

设S为个体空间，SN为种群空间，P为SN上的概率分布，｛（n）｝是遗传算法所生成的第n代种群序列，f：s→R＋为适应值函数，记全体最优解集为M＝｛X；∀Y∈S有f（X）≥f（Y）｝．

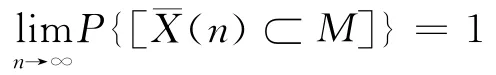
定义2 （几乎必然收敛）称种群序列｛X¯（n）｝几乎处处弱收敛到全局最优解集M，若

从上述的定义可以看出，如果遗传算法收敛，不管是依概率收敛还是几乎必然收敛，不管是强收敛还是弱收敛，必定存在种群序列｛¯X（i）｝，该序列与最优解集的交集不为空集，并且，这样的种群序列不止一组［5－8］．

在计算过程中，如何判断种群序列｛¯X（i）｝与最优解集的关系是判断是否停止迭代的重要依据．而如何确定问题的最优解集或者最优解又是分析上述关系的关键．

2 停机准则研究

2.1 不同种群最优个体适应值的一致性

通过对遗传算法种群序列收敛的定义及其特点的分析，可以看出收敛的遗传算法能够到达最优解集．如果种群序列｛¯X（i）｝到达最优解集，并且该算法采用最优个体保留策略，对于序列｛¯X（k）；k＞i｝，则必含最优解集的值，即使不采用最优个体保留策略，在第i代以后的种群中，必然还将存在能够到达最优解集的序列．将第i代种群序列的最优个体适应值记为fmax，i，并将其存放在集合B中．

通常情况下，某个体在多代种群中被作为最佳个体而被保存下来，则说明该个体具有优良的基因，其适应自然的能力极强而不致被淘汰，其个体最接近或者就是问题的最优解．反映到算法中，设集合B大小为m，将第一代种群序列｛¯X（1）｝的最优个体适应值fmax，1存入集合B中，然后进行遗传操作，得到的下一代种群序列｛¯X（2）｝的最优个体适应值记为fmax，2，存入集合B中，依次进行下去，直到将集合B存满为止．将集合B中不同种群最优个体适应值的一致性记为R．

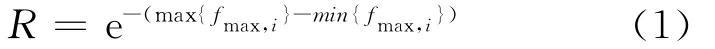
如果B已经存满而所得R值不能满足要求，则继续进行遗传操作运算，如果获得的fmax，m＋1比B中较差个体适应值更优，则将fmax，m＋1取代B中的最小值，依次进行下去，直到所得结果满足要求为止．

R值在一定程度上反映了种群最优个体适应值作为最优解的可信度，当m取较大的值并且R值趋于1时，说明不同种群最优个体的适应值一致性较强，取B中的最大值作为问题的最优解的可信度比较的大．在实际应用中，m值依具体情况而定．

然而，仅采用不同种群最优个体适应值的一致性判断算法达到最优解容易使算法陷入局部极值而停止迭代，故需考虑种群的多样性．

2.2 种群的多样性

遗传算法在计算过程中对包含可能解的种群反复使用遗传学的基本操作，不断地生成新的种群，并以全局并行搜索技术来搜索问题域中的最优个体，以求得满足要求的最优解或准最优解．遗传算法在运行的过程中可能会暂时停留在某些非最优点上，直到变异发生使其跃迁到另一个最优点上．由此可以断定，随着种群多样性的增加，在上述不同种群个体最优值的一致性为1的情况下所得的最优解作为全局最优解的可信度更大．

种群的多样性不是指一代种群，而是指到停时为止所有种群个体的多样性．设当代种群中包含不同个体数目记为其中k为种群中个体所在的位置，N为种群规模．当遗传算法迭代n次后，所有种群所包含的不同个体的数目为所有种群的多样性记为V．

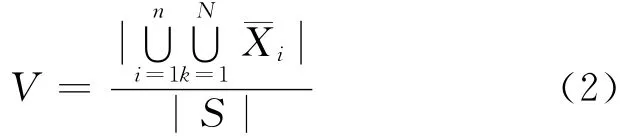
V值一定程度上反映了算法搜索域在整个问题的可行解域中所占的比例，当V值趋于1时，说明遗传算法搜索了所有的可行解，这样，所得到的最优个体必然是问题的最优解．

在实际的计算中，采用式（2）会使算法的复杂度大大增加．对实际问题，可以考虑将个体空间进行 划 分 h 块，令 S记 δi＝如此，则V可简化为

2.3 停机准则

设遗传算法的停机判断因子为η，η表达式如下

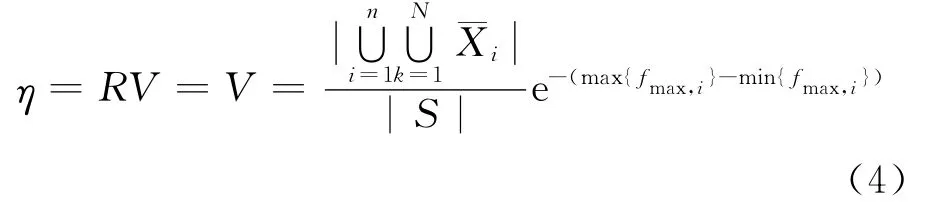
当η→1时，算法停止迭代，所得的计算结果可作为问题的最优解．上式中没有用到具体的编码方式，仅从不同种群最优个体适应值、种群的多样性出发研究停机准则，故该式的适用范围较广．在实际的应用中，B中所包含元素的个数以及可行域的划分影响所得结果的可信度，需着重考虑．

对于标准遗传算法，通过马氏链模型可以看出，该算法不能保证得到全局最优解，然而可以达到种群空间中任何状态无限多次，如此，从上述停机判断角度分析，标准遗传算法的停机判别因子η能够无限接近于1，故从实用的角度来讲，标准遗传算法是有效的．

2.4 数值实验

为验证本文所提出的遗传算法停机准则的可行性，下面给出求De Jong函数和Shubert函数最小值的实验，并与不采用该停机准则所计算的结果进行比较．

1）De Jong测试函数

遗传算法的主要参数：采用二进制编码，个体数量100，适应度比例选择算子，交叉概率0．7，变异概率0．035，停止迭代次数分别设置为100，200，300，400，各个迭代次数计算5次，取最小值．所得结果见表1．如果采用停机准则，遗传算法参数不变，最优解｜B｜＝80，区间划分为203个，η＝0．999 9，计算3次，结果见表2．

表1 设定的迭代次数与函数最小值

表2 满足条件自动停止的迭代次数与函数最小值

2）Shubert测试函数

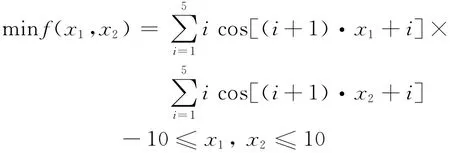
遗传算法的主要参数：采用二进制编码，个体数量50，适应度比例选择算子，交叉概率0．7，变异概率0．03，停止迭代次数分别设置为20，30，40，50，各个迭代次数计算5次，取最小值．所得结果见表3．如果采用停机准则，遗传算法参数不变，最优解｜B｜＝10，区间划分为100个，η＝0．999 9，计算4次，结果见表4．

表3 设定的迭代次数与函数最小值

表4 满足条件自动停止的迭代次数与函数最小值

从该实验中，可以看出，利用停机准则设置算法停止迭代的条件，实现了目标函数达到最优解后自动停机的目的．

3 结束语

从遗传算法收敛性定义出发，研究了遗传算法的自动停机准则，从式（4）中可以看出，该准则只与不同种群最优个体适应值、种群多样性有关，使得该公式有较广的适用范围．停机判断因子反映了遗传算法所求问题最优解的可信度，η越接近于1，则所求最优解的可信度越高．而在停机判别因子及各个参数的设置上，需根据具体需要加以适当限定．同时，该停机准则为建立恰当的度量标准来客观评价遗传算法的各种执行策略及时间复杂度提供参考．

［1］田雨波，钱 鉴．计算智能与计算电磁学［M］．北京：科学出版社，2008．

［2］AYTUG H，KOEHLER G J．Stopping criteria for finite length genetic algorithms［J］．INFORMS Journal on Computing，1996（8）：183－191．

［3］PARAG C P，GARY J K．A general steady state distribution based stopping criteria for finite length genetic algorithms［J］．European Journal of Operational Research，2007，176：1436－1451．

［4］邝溯琼．遗传算法参数自适应控制及收敛性研究［D］．长沙：中南大学，2009．

［5］张文修，梁 怡．遗传算法的数学基础［M］．西安：西安交通大学出版社，2003．

［6］毕晓君，肖 婧．基于自适应差分进货的多目标进化算法［J］．计算机集成制造系统，2011，17（12）：55－58．

［7］朱葛俊．基于差分进化和粗糙集理论的多目标优化算法的研究［J］．科技通报，2012，28（2）：80－84．

［8］李 珂，郑金华．一种改进的基于差分进化的多目标进化算法［J］．计算机工程与应用，2008，44（29）：40－43．