Research on Three-Echelon Inventory Model and Algorithm for Valuable Spare Parts in Weapon Equipment

SUN Jiang－sheng(孙江生)，ZHAO Fang－geng(赵方庚)，LV Yan－mei(吕艳梅)，LIAN Guang－yao(连光耀)

(1.Machine Technology Research Institute，Shijiazhuang 050000，Hebei，China;2.Bengbu Automobile Petty Officer Academy，Bengbu 233011，Anhui，China)

Introduction

Spare parts delivery is an important and difficult problem in weapon equipment support.It is always besetting the weapon equipment support to determine the ordering strategy and the stock level and obtain the best military and economic efficiency.Currently，in our country，the expenditure rules of spare parts are studied to constitute the dissipative standard of spare parts，and the modern supply chain theory has been applied to the model research of the spare parts support.However，the significant achievements about the spare parts support theory，especially the multi－echelon inventory optimization theory，are singularly because of the complexity of the problem.In the foreign countries，the spare parts support are usually modeled as a repairable inventory model，and many researches，including the single－echelon and multi－echelon inventory models，aimed at the valuable and seldom－available spare parts.In addition，the multi－indenture relationship between spare parts and the cannibalization issue are also thoroughly discussed.The related research results have already been applied to the equipment support of the Army，Navy and Air force in the US［1－7］.

Although researches about the inventory for reparable spare parts are abundant，no one of them can be well applied to the practical equipment support in PLA，especially to the practical environment of multi support layer and the complex composition of support power.In this paper，based on the two－echelon inventory model for repairable spare parts that is widely studied abroad，a three－echelon inventory model for valuable spare parts，which is more fit to the practical environment in PLA，is established，and the genetic algorithm for the problem solution is studied to obtain the inventory strategy.

1 Physical Model for Three-echelon Inventory

In this paper，the spare parts are assumed to be valuable and non－often－used，and optimizing the inventory of these parts will significantly affect the weapon supply.The inventory model of valuable spare parts will be based on the sketch shown in Fig.1，and the physical process of repairing valuable spare parts can be described as follows.

Fig.1 Sketch of repair organization and spare part provision for weapons

When the using unit detects a fault of equipment，the maintenance organization in the basic level should do some simple works，such as failure isolation，recognition and disassembly operation，and repairing simple fault etc.If it can not fulfill the repair work，then send the fault spare parts to the intermediate maintenance organization for repair，and ask the intermediate level supply the parts.The intermediate maintenance organization repairs the fault spare parts sent from the basic levels belonging to it，and the spare parts will be stocked at the intermediate level or supplied to the relevant basic level after repair.If the parts can not be repaired by the intermediate maintenance organization，it will be sent to the base for repair，and the base will be asked a supply demand.The base repairs the parts sent from the intermediate level，and keeps a certain stock level to supply the intermediate maintenance organization.When the base and the intermediate level receive the request of re－supply，the time of ordering and transporting will be considered as the time from that the supply requirement is sent by a lower level to that the item is obtained from its higher level organization.The model can calculate the delay when the higher level supplies to the lower level，which depends on the stock level of the higher level.

According to the practical environment of equipment support in PLA，the following assumptions are made in the model.

1)The(s－1，s)inventory policy is appropriate for each part in every echelon.It means that the parts are not batched for repair，and any fault parts are repaired one by one.

2)If the basic levels have test equipment，persons and other resources，and the repair is accomplished with a probability，whenever the base has the capability，without considering workload.

3)The lower level is supplied from its higher level，and the lateral supply from the same level is not permitted.It appears to be appropriate for set stock levels，because the number of lateral shipments is typically small and they are apt to induce special transportation costs.

4)The stock，transportation and related management costs are not considered in the model.

5)The base can not directly supply the spare parts to the basic levels，and the intermediate level can only supply the spare parts to its basic levels.

Compared to the classic METRIC model，the variables in the three－echelon model significantly increase，and the number of optimizing calculation exponentially augments.

2 Modeling

In our three－echelon inventory model for valuable spare parts，only random faults are considered.According to the Palm’s theory［8］，if the demand of a part is according with Poisson distribution with a annual expectation of m，and the time for repairing each fault part is independent and has the same distribution with a mean of T years，the distribution for the quantity of parts under repair is a Poisson distribution with an expectation of mT.That is

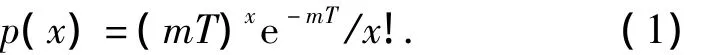
According to the classical METRIC theory，the expression of stock level is

where s is the stock level of a spare part，OH denotes the stock quantity of spare parts in the field，DI represents the stock quantity of spare parts obtained from repair or re－supply，and BO is the delayed delivery quantity.All of the quantities mentioned above are the non－negative random variables，and any change of a variable will change other parameters.

Let’s assume that the expected quantity of spare parts is s+k in a certain random time，from Eq.(2)，we can see that the delayed delivery quantity is k，and its expectation can be written as

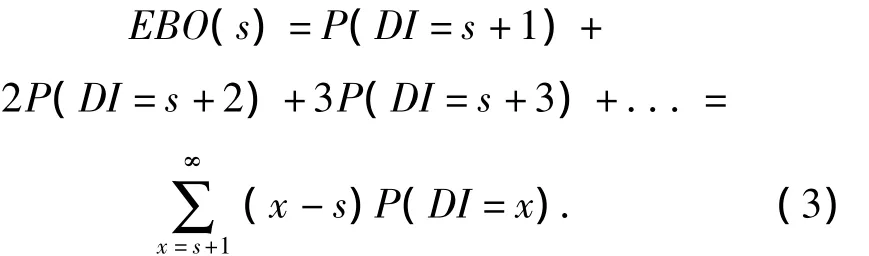
From Eq.(3)，we can determine the mathematical expectation of the delayed delivery quantity at different stock level.For any valuable spare parts，the variables in the three－echelon inventory model can be set as follows:

m0the average annual demand in the base;

T0the average repair time in the base.

As the sum of several Poisson distributions is a Poisson distribution also，we can firstly calculate the average demand in the base，which is a sum of the demands that can not be repaired in the intermediate level.Assume that the total number of the intermediate level organizations is I，then

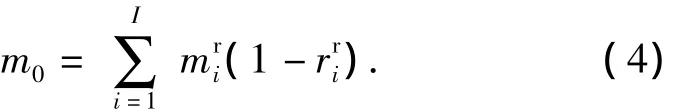
The average demand in the intermediate level i is a function of demands that can not be repaired in the basic level j belonging to the intermediate level organization.Assume that the total number of basic levels belonging to the intermediate level i is J，then

The average pipeline of the demand in the basic level j can be expressed as

If the item can be repaired in the basic level，then the average pipeline in the basic level j isthat is，the quantity of the under－repair units in the basic level.If the item can not be repaired，then the average pipeline isbecause it is caused by the ordering and transporting time，and the delayed delivery caused by the fact that the intermediate level has not stock always.The expected delayed delivery in the intermediate level i，EBO ()，is the expectation of re－supply demand from the basic level which can not be completed in the intermediate level i at any time.Another explanation for this quantity is that it is the average quantity of accumulating delay of daily resupplies demand because the intermediate level can not always possess the stock.

Finally，the average pipeline of each demand in the intermediate level i can be written as

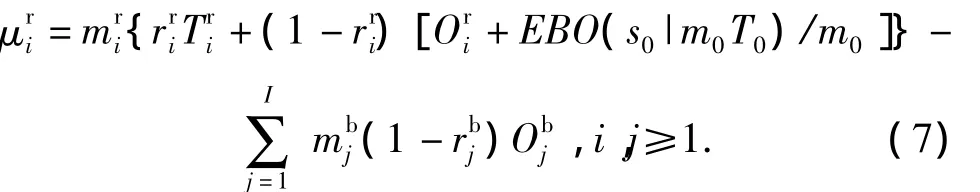
If the part can be repaired in the intermediate level，the average pipeline in the intermediate level i is，which is the average quantity of under－repair parts.If it can not be repaired，the average pipeline is，because this quantity is caused by the ordering and transporting time，and the delayed delivery caused by the fact that the basic level has not stock always.The expected delay delivery in the base，EBO(s0|m0T0)，is the expectation of the re－supply demand from the intermediate level which can not be completed in the base at any time.

In addition is the average pipeline that the intermediate level i intends to supply to each basic level j belonging to it.The average pipeline is a dimensionless parameter，and it can be understood as:Eq.(1)the average expectation during a longer period of time，or Eq.(2)the average expectation in many different random time periods.

Note that many parameters are not necessary in the optimization process in discussing the model.For example，the ordering and storage costs are not taken into account，because they are assumed to be supplied one by one，which means the ordering quantity and the field average stock have been determined already.The repairing cost is not considered also，because，if a part can be repaired，the cost for repair is far less than that of purchasing a new one.

In a word，we can determine the expected delay delivery at different stock level by Eq.(1)and Eq.(3 －7).If the expected delay delivery decreases，the system availability， as mentioned by Sherbrooke［8］，will increase.In the established three－echelon inventory model，the optimization objective is to maximize the system availability under the constraint of total cost.

3 Genetic Algorithm for the Three-Echelon Inventory Problem Solution

Currently，METRIC－based models are mainly solved by marginal analysis proposed by Sherbrooke，and it is a greedy local search method with lower efficiency［9］.To improve the performance of inventory assignment algorithm，we use the genetic algorithm(GA)to solve the three－echelon inventory problem of repairable spare parts.

Genetic algorithm is a search algorithm based on an evolutionary principle.It was firstly proposed by Holland［10］.It has been successfully applied to many combinatorial optimization problems，such as the traveling salesman problem(TSP)［11］，the vehicle routing problem(VRP)［12］，the quadratic assignment problem(QAP)［13］， and the job－shop scheduling problem(JSP)［14］，because of its simplicity，ease of operation，and global perspective.

GA’s flowchart for the three－echelon inventory problem solution is shown in Fig.2.After initializing the parameters used in the algorithm，GA produces an initial population comprised of pop_size feasible solutions，and then evaluates each solution’s fitness with the objective function.As long as the terminal condition is not satisfied，GA searches iteratively.In each iteration(generation)，two individuals are randomly selected from the population according to the roulette wheel selection rule.Then，the selected individuals are operated by using crossover and mutation operators to generate offspring.After the operations mentioned above，half of the individuals with worse fitness in population are replaced by the offspring，and the size of population keeps constant.In addition，the stopping criterion used in our algorithm is defined in terms of a fixed number of generations.

Fig.2 Flowchart of genetic algorithm for three-echelon inventory problem

3.1 Chromosome Representation and Fitness Evaluation

We use an integer string of length(IJC+JZJ+1)×l to represent the chromosome，where IJCis the total number of basic level organizations，JZJis the total number of intermediate level organizations，and l is the total item of spare parts.Fig.3 gives an example chromosome with 1 base，2 intermediate level organizations，6 basic level organizations，and the equipment has 3 spare parts.In the solution shown in Fig.3，the stock level of part 1 in the base is s10，the stock level of part 2 in the first intermediate level organization is s21，and the stock level of part 3 in basic level 5 is s37.

The fitness of a chromosome(solution)shows its solution quality.In our algorithm，the overall system availability，under the corresponding inventory assignment scheme，is used to evaluate the fitness.

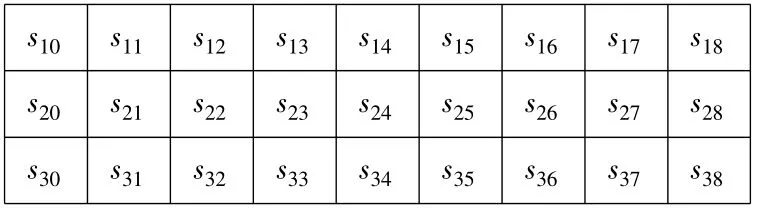
Fig.3 Chromosome representation

3.2 Production of Initial Population

The production method of initial population is based on the random selection.The production algorithm randomly selects a part x and an inventory location y，and adds 1 to the corresponding stock level.This random selection procedure will be iterated until the total investment can not afford to add more spare parts.The procedure is repeated pop_size(the size of population)times.

3.3 Crossover Operator

The crossover operator utilizes two parents(p1，p2)to construct an offspring.Before generating an offspring，the operator firstly calculates a factor fc

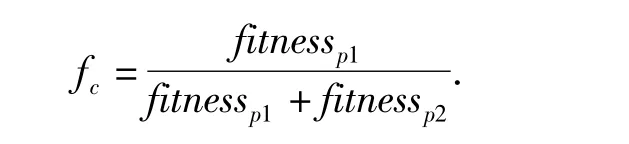
Let s'xyrepresent the stock level of part x in location y in solution p1，and s″xyrepresent the stock level of part x in location y in solution p2.The corresponding stock level sxyin the offspring is

Step 1:Randomly select a part x and an inventory location y;

Step 2:If sxyis larger than the corresponding stock level in the better solution of the two parents，then sxy=sxy－1，and go to Step 3;otherwise，return to Step 1;

Step 3:If the offspring is feasible，then end the adjustment，otherwise，return to Step 1.

3.4 Mutation Operator

Let total_cost represent the total cost of all spare parts in a solution，cxdenote the cost of part x.The mutation process is:

Step 1:Randomly select two element，sxyand skr，in the solution;

Step 2:If(total_cost+cx－ck)＜C，then sxy=sxy+1，skr=skr－1，and total_cost=total_cost+cx－ck;otherwise，sxy=sxy－1，skr=skr+1，total_cost=total_cost－ cx+ck.

4 Computational Example

4.1 Algorithm Implementation and Parameter Setting

The genetic algorithm is implemented in C under a Visual C++ .net environment.The population size pop_size is set to 30，the crossover probability and the mutation probability are set to 0.8 and 0.1，respectively.In addition，the algorithm will be stopped after 100 generations.

4.2 Instance and Results

An instance of three－echelon inventory problem for valuable spare parts involves 1 base，3 intermediate level organizations，9 basic level organizations(each intermediate level organization dominates 3 basic level organizations)，and 10 different spare parts.The parameters for the problem are set as follows.

The number of equipment in the basic level organizations(Nj)×9=(10，10，10，10，10，10，10，10，10);

The average annual demands of the basic level for spare parts(mij)×10×9=(12.1，6.6，11.2，5.9，13.2，13.6，10.8，7.2，12.5，12.3)×9;

The price of parts(ci)×10=(120，100，155，85，167，221，77，122，189，356).

The number of part occurrences in the equipment(Zi)×10=(1，2，1，3，2，1，1，1，2，1).

In addition，the average repair times for spare parts in the basic level，intermediate level organizations and base are 0.01，0.016 and 0.02 years，respectively;the repair probability in the basic and intermediate levels is 0.3 and 0.5，respectively，and the average ordering and transporting times both from base to intermediate level and from intermediate level to basic level are 0.01 years.

The problem is solved under different investments(C=2 500，5 000，…，30 000)，and the relation between investment and availability is given in Fig.4.Take C=2 500 for an example，the inventory assignment results are shown in Tab.1.

Fig.4 Relation between investment and availability

Tab.1 Inventory assignment scheme when C=2 500

5 Conclusions

In this paper，based on the repairable inventory theory，the repair and supply support of weapon equipment in PLA，a three－echelon inventory model for the valuable spare parts is established.In this model，the relationship between the ordering cost and the delayed delivery is discussed.To solve the model，the genetic algorithm for three－echelon inventory problem is designed.By using the model and algorithm，the spare parts stock and supply strategy can be optimized in a three－echelon situation.

［1］Giillii R.On the value of information in dynamic production/inventory problems under forecast evolution［J］.Na－val Res.Logist，1996(43):289 －303.

［2］Heath D C，Jackson P L.Modeling the evolution of demand forecasts with application to safety stock analysis in production/distribution systems［J］.IIE Transcations，1994，26(3):17－30.

［3］Stephen C G.A multi－echelon inventory model for a repairable item with one－for－one replenishment［J］.Management Science，1985，31(10):1247－1250.

［4］Vinayak Deshpande，Morris A Cohen，Karen Donohue.An empirical study of service differentiation for weapon system service parts［J］.Operations Research，2003，51(4):518－521.

［5］Perlman Y，Mehrez A ，Kaspi M.Setting expediting repair policyin a multi－echelon repairable2item inventory system with limited repair capacity［J］.Journal of the Operational Research Society，2001，52(2):198－209.

［6］Rustenburg W D，van Houtum G J，Zijm W H.Spare parts management for technical system:Resupply of spare parts under limited budgets［J］.IIE Transactions，2000，32(10):1013－1026.

［7］Kim J S，Shin K C，Park S K.An optimal algorithm for repairable－item inventory system with depot spares［J］.Journal of the Operational Research Society，2000，51(3):350－357.

［8］Sherbrooke C C.Optimal inventory modeling of systems:Multi－echelon techniques［M］.2nd ed.Boston:Artech House，2004.

［9］Díaz A.Multi－echelon inventory models for repairable items［M］.College Park:University of Maryland，1995.

［10］Holland J.Adaptation in natural and artificial systems［M］.Ann Arbour:The University of Michigan Press，1975.

［11］Nguyen H D，Yoshihara I，Yamamori K，et al.Implementation of an effective hybrid GA for large－scale traveling salesman problems［J］.IEEE transactions on Systems，Man，and Cybernetics，Part B:Cybernetics，2007，37(1):92－99.

［12］Prins C.A simple and effective evolutionary algorithm for the vehicle routing problem［J］.Computers ＆ Operations Research，2004，31(12):1985 －2002.

［13］Misevicius A.An improved hybrid genetic algorithm:new results for the quadratic assignment problem［J］.Knowledge－Based Systems，2004，17(2 －4):65 －73.

［14］Park B J，Choi H R，Kim H S.A hybrid genetic algorithm for the job shop scheduling problems［J］.Computers＆ Industrial Engineering，2003，45(4):597－613.