基于改进的相关度的局部图像修复模型
2012-03-07胡德敏朱晓临邓祥龙
胡德敏, 朱晓临, 邓祥龙
(合肥工业大学 数 学学院,安徽 合 肥 230009)
图像修复是指对数字图像中丢失、破损的部分进行还原修复,是一种出现很早的工艺技术,近年来图像修复技术有了长足的发展。图像修复主要应用于破损图像的恢复以及文字或物体等目标区域的移除,主要有基于纹理的修复方法和基于结构的修复方法。目前结构的修复模型大多基于偏微分方程(partial differential equation,简称PDE)或变分问题(variation formulation)。有研究者提出了基于纹理的图像修复方法,在未受损图像中寻找与受损模块最为匹配的修复模块并填充到受损区域内,从而实现图像的修复。
文献[1]将PDE方法应用于图像修复,该模型依据艺术家修复图片的方法,沿图像等照度线方向将已知区域的信息传输到待修复区域,由于等照线之间无信息交互,因此该模型还附加各向异性扩散过程来保证等照线间信息交互以保持模型的稳定。
文献[2]提出了基于整体变分(Total Variation,简称TV)模型的图像修复方法,也是一种比较好的各向异性扩散算法,在保持边缘的同时达到去噪的目的。但是这种方法对于修复条形或线形来说运算量比文献[3]算法的运算量大,且对参数的选取也较敏感。文献[4]提出了曲率驱动扩散模型(curvature driven diffusion,简称CDD),这种模型把曲率考虑进去,虽然修复效果有所提高,但运算量比较大。此外,这种方法在修复图像中可能产生人为的角点。
文献[3]对整体变分模型进行改进,提出对条形或线形空白区域图像修复算法。该算法对一定宽度的竖条形修复效果较好,但应用范围比较局限,主要适用于宽度约为10个像素,长度约为120个像素的待修补区域。
文献[5]提出了一种改进的整体变分法并且将其应用到图像修复中,通过考虑图像破损区域外部参考像素和待修复点的相关度,从而达到图像修复的目的。
文献[6]通过在图像修复迭代过程中设置不同的参数,解决参数选取敏感的问题,从而达到修复效果。此方法对于2个破损区域处于同一行或者同一列的时候修复效果不太理想。
文献[7]通过对TV模型进行改进,采用由外到内的修复顺序,并完全采用已知区域信息对图像进行修复,所有待修复点仅需1次迭代便可完成修复。该方法对于那种破损区域只有几个像素宽的图像修复效果理想,但对破损较大的区域修复效果不太理想。
传统的TV模型在修复图像时,都是对整个待修复图像进行迭代,本文通过找出待修复图像的破损块,并只在该破损块上进行迭代,提出局部图像修复模型,减少了图像修复所需时间。同时引入改进的相关度,使图像的修复效果更好。
1 TV模型简介
TV(Total Variation)模型[2]由 T.F.Chan于2000年提出,其后又有很多学者对这一模型进行了改进[8-10]。图1所示为破损区域及其邻域示意图,其中D为待修复区域(空信息),E为待修复区域的外区域,一般为环状。
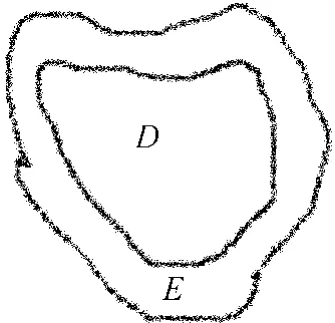
图1 待修复图像
记修复后区域D∪E内的图像为u,定义代价函数为:

且满足噪声约束:

其中,A(E)为E的面积;σ为白噪声的标准差;r为非负的实函数;▽u为图像u灰度的梯度;u0为E内被白噪声污染的原始图像。
(1)式使待修复区域及边界尽可能平滑,(2)式使修复过程对噪声有良好的鲁棒性。运用Lagrange乘子法将有约束条件的极值问题转化成无约束条件的极值问题,新的代价函数为:

根据Euler-Lagrange方程知,使得Jλ(u)最小的u应满足如下条件:

在实际计算中,为防止分母过小,div(▽u/|▽u|)通常需要转换为div(用|▽u|a表示,则(4)式变为:

本文只考虑没有加入高斯噪声的干扰,那么(5)式变为:
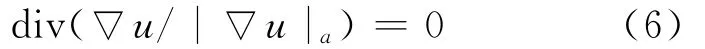
(6)式为TV模型的基本公式。
2 基于相关度的TV模型
相关度的概念由文献[5]提出。传统的修复方法只是考虑了上下左右4邻域参考点对目标点的影响,而没有考虑目标点与它们的距离远近对修复效果的影响。而相关度在修复时考虑到破损区边缘各个参考点对目标点的影响不同,对每个参考点设置权值来区分它们分别对目标点的影响程度,如图2所示。
其中,A为破损区域的外围部分;B为破损区域,破损区域B内为空信息。
文献[5]中的相关度Ri定义为:

其中,参数r1、r2、r3、r4分别为目标点O距左右上下4个方向参考点V1、V2、V3、V4的距离(距离取目标点与参考点间的相隔像素数)。

图2 目标点与参考点的相关度系数
3 基于改进相关度的图像修复模型
由(7)式可以看出距离目标点越近,该参考点对目标点的影响越大,反之则影响越小。从(7)式中r-1i可以看出,当参数r越小,则它的倒数就大,即与参考点的相关度越大。如果把它的指数-1换成-ri,相当于强化了相关度的作用,那么在相同的迭代次数下,这种改进的相关度对图像修复效果的影响将更明显。
改进的相关度定义为:

其中,参数r1、r2、r3、r4分别为目标点O距左右上下4个方向参考点V1、V2、V3、V4的距离(距离取目标点与参考点间的相隔像素数)。
特别地,当破损区域为细长的竖条形状时,不考虑上下参考点对目标点的影响,此时改进的相关度为:

当破损区域为细长的横条形状时,不考虑左右参考点对目标点的影响,此时改进的相关度为:

图3、图4所示为文献[5]基于相关度的模型和本文基于改进相关度模型的修复效果对比。
图3、图4是迭代500次的修复效果图,从这2组图对照来看,基于改进的相关度的模型比基于相关度的模型的修复效果好,修复时间也差不多,见表1所列。

图3 本文与文献[5]的修复效果对比(一)

图4 本文与文献[5]的修复效果对比(二)

表1 图3、图4所需修复时间对比
4 基于改进相关度的局部图像修复模型
传统的TV模型都是在整个待修复图像上进行迭代修复,这样图像修复所需的时间就比较长。为此,本文提出局部图像修复模型,即通过在整幅图像上寻找破损区域,并且只在该破损区域进行迭代修复,这样就大大减少了图像修复所需的时间。具体地说就是:先在整幅图像上搜寻待修复点,通过待修复点向上下左右4个方向继续寻找破损点,进而找出破损区域的最大长和宽,然后再通过长宽计算出该破损区域,在该破损区域运用基于改进的相关度的图像修复模型进行迭代修复。这样,在缩短图像修复所需时间的同时又提高了图像的修复效果。
在图5中,O为待修复点,本文的模型考虑O的8个邻域的像素信息,采用半点格式法来求解梯度。

图5 8邻域图
设O的邻域节点为Λ={N,S,W,E},{n,s,w,e}为O的半像素邻域点。半点n点像素的梯度为:

半点e、s、w点像素的梯度可类似给出。
根据上述分析,提出基于改进的相关度的局部图像修复模型,记

其中,v1和v2分别表示▽u/|▽u|在待修复区域横向和纵向的分量,则(6)式可以离散化为:
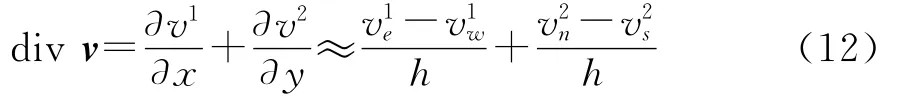

其中,divv表示v的散度。以v2n为例,即可类似推出。把(11)~(13)式以及改进的相关度R1、R2、R3、R4带入(6)式可得:

解得:
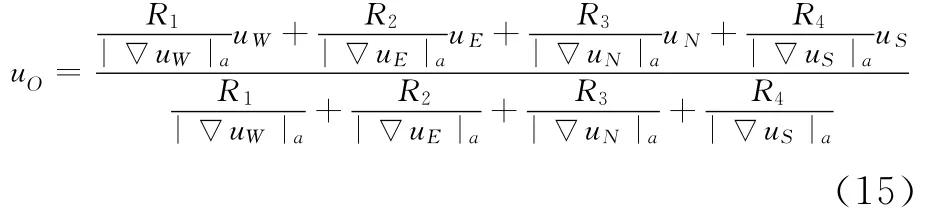
考虑到破损区域可能是细长横条或细长竖条,为了将这些特殊情形也包含在(15)式中,将(15)式改写为:

其中,ki=1或0,i=1,2,3,4。应用 G auss-Jacobi 迭代算法,则图像u可以由(17)式求得:

在(17)式中,当破损区域为细长横条时,k1=k2=0,k3=k4=1,此时改进的相关度为
当破损区域为细长竖条时,k1=k2=1,k3=k4=0,此时改进的相关度为
当破损区域不是上述2种情形时,则k1=k2=k3=k4=1,改进的相关度由(8)式给出。
方法步骤如下:
(1)读取待修复图像。
(2)在整幅图像上寻找待修复点,并计算待修复点到上下左右的距离,得到局部破损区域的最大长和宽,寻找到该破损区域D,同时利用(8)~(10)式计算改进的相关度Ri。
(3)确定破损区域D外边缘2像素宽的环状区域E。
(4)通过(17)式对该破损区域进行局部修复。
(5)当一个破损区域修复完成以后返回到步骤(2),继续进行修复,直到图像完全被修复后停止。
5 实验结果
本文采用峰值信噪比(PSNR)对所修复图像进行评估。所修复图像的PSNR值越大,则修复效果越好。其中,U为原图像;U1为修复后的图像;M和N为图像的行列值。
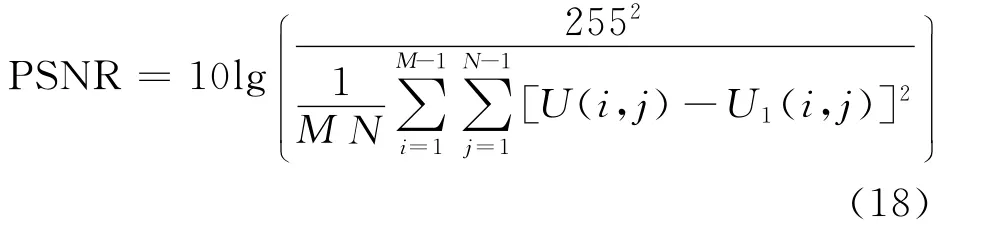
图6、图7所示为本文的模型、TV模型和文献[5]中改进TV模型的图像修复效果,PSNR值和修复时间的比较见表2所列。

图6 本文的模型与TV模型和文献[5]中改进TV模型的比较(一)

图7 本文的模型与TV模型和文献[5]中改进TV模型的比较(二)

表2 本文模型与现有模型的PSNR、修复所需时间对比
由表2可知,本文给出的基于改进的相关度局部图像修复模型比TV模型和文献[5]中的改进的TV模型对图像的修复效果更好,所用的时间也更短。
6 结束语
本文通过对传统的TV模型进行分析,并在文献[5]方法的基础上,引入改进的相关度,提出针对局部破损区域进行修复的基于改进的相关度的局部图像修复模型。此模型大大地缩短了修复图像的时间,而且得到了更好的修复效果。通过实验可以得出,在迭代次数相同的情况下,本文给出的基于改进的相关度的局部图像修复模型比传统的TV模型和文献[5]中改进TV模型对图像的修复效果更好,所用的时间也更短。
[1] Bertalmio M,Sapiro G,Caselles V,et al.Image inpainting[C]//Proceedings of SIGGRAPH’2000.ACM Press,2000:411-424.
[2] Chan T F,Shen J.Mathematical models for local nontexture inpaintings [J].SIAM Joumal on Applied Math,2001,62(3):1019-1043.
[3] 郑精灵,王树根.整体变分算法在图像修补中的应用研究[J].计 算 机 辅 助 设 计 与 图 形 学 学 报,2003,15(10):1219-1223.
[4] Chan T F,Shen J.Non-texture inpainting by curvaturedriven diffusions(CDD)[J].Journal of Visual Communication and Image Representation,2001,4(12):436-449.
[5] 周 密,彭进业,赵 健,等.改进的整体变分法在图像修复中的应用 [J].计算机工程与应用,2007,43(27):88-90.
[6] 许云云,朱晓临,黄淑兵,等.基于TV模型的改进算法在图像修复中的应用[J].合肥工业大学学报:自然科学版,2010,33(12):1916-1920.
[7] 朱 坤,朱晓临,许云云,等.一种快速的图像修复算法[J].合肥工业大学学报:自然科学版,2011,34(8):1272-1275,1280.
[8] 邵肖伟,刘政凯.一种基于TV模型的自适应图像修复方法[J].电路与系统学报,2004,9(2):113-117.
[9] 张福美,潘振宽.基于整体变分模型的矢量图像修复[J].计算机工程,2008,34(8):223-225.
[10] 邢天璋,彭进业.一种改进的全变分(TV)修补模型[J].西北大学学报:自然科学版,2009,39(6):948-951.
