倾斜荷载下基桩P-Δ效应等效剪力有限元迭代法研究

李微哲

（中煤科工集团重庆设计研究院，重庆 400016）

倾斜荷载下基桩P-Δ效应等效剪力有限元迭代法研究

李微哲

（中煤科工集团重庆设计研究院，重庆 400016）

假定桩身位移为三次幂函数，结合倾斜偏心荷载下单桩受力微分方程确定的桩身弯矩、剪力与桩身水平位移关系，在此基础上引入等效剪力增量概念，提出了基桩P-Δ效应的等效剪力有限元迭代法，相应编制了Matlab分析程序，并结合算例对成层地基中倾斜偏心荷载、桩自重、水平分布荷载、竖向分布荷载和竖向荷载综合作用下基桩内力位移进行了分析。结果表明：等效剪力有限元迭代法用于倾斜荷载下基桩P-Δ效应计算分析是有效的；当墩身较高时，墩身倾斜、墩顶偏心弯矩、水平力等对基桩产生的P-Δ效应显著。

桩基础；倾斜荷载；等效剪力有限元迭代法；P-Δ效应

在倾斜偏心荷载下，不仅其水平分力和偏心矩将使桩身产生较大内力和位移，竖向分力也将因桩身挠曲变形而产生附加弯矩，即所谓的P-Δ效应。

P-Δ效应在工程中备受关注。从上世纪50年代以来国际著名学者Meyerhof对倾斜荷载下基桩承载力性能进行了大量的室内模型试验研究，提出了倾斜偏心荷载下单桩承载力计算的半经验公式，然而倾斜荷载下计入P-Δ效应的基桩内力及位移分析研究不多［1-5］。随后，国内外学者对计入P-Δ的基桩内力及位移分析做了大量研究工作。70年代横山幸满给出了地基系数为常数时的幂级数解析解［6］；赵明华等给出了地基系数m法假定的幂级数解析解，提出了有限元－有限层法、引入加权刚度的改进有限元－有限层方法［7-10］；笔者给出了地基系数满足（mz+C）的线性增长规律时的幂级数解析解［11］。

但在计算机普及的时代，探讨计入P-Δ效应的基桩内力及位移分析有限元法，有重要的实际意义。为此提出了等效剪力有限元迭代法，进行倾斜荷载下基桩计算分析研究，以进一步探讨计入P-Δ效应的基桩受力特性。

1 等效剪力有限元迭代法

1.1 考虑P-Δ效应的单元平衡方程

对倾斜偏心荷载下基桩微元体进行受力分析（见图1），弯矩以桩身左侧受拉为正、剪力以构成顺时针力矩为正、位移向右为正、桩侧土压力右侧受压为正，从桩段中取出一微元体对下端点取矩得弯矩平衡方程如下

式中：P(z)为轴力；Q为剪力；M为弯矩；dM为剪力增量；dz为基桩微元体长度；q为侧向均布荷载。

对式（1）进行简化可得

式中：dv为桩段单元水平位移差。

1.2 模拟附加弯矩的等效剪力

1.3 基桩P-Δ效应过程模式假定

如图2，假定单桩顶作用有水平力FQ和竖向力Fz，不考虑P-Δ效应时，桩身将发生水平位移，节点i初始位移为Vi0，所有节点的位移列阵记为V0。所有水平力和弯矩构成的节点荷载列阵记为Q0。则有

式中：K为初始刚度矩阵；k为节点约束等效弹簧刚度矩阵；V0为初始位移列阵；Q0为初始荷载列阵。

此时竖向力Fz因桩身发生的初始水平位移而产生附加弯矩，假定节点i、节点i+1处的等效剪力增量为Qi1，Q(i+1)1计算如下

式中：Qi1为i点第一次等效剪力增量；Q(i+1)1为第i+1点第一次等效剪力增量；Fzi，Fz(i+1)分别为i点和i+1点的竖向力。

将第一次等效剪力增量Q11，Q21，…，Qi1，Q(i+1)1记为Q1。在Q1作用下，桩身继续发生变形，将此时的位移增量记为V1。竖向力Fz因变形增量V1将继续产生附加弯矩，设此时节点i、节点i+1处的等效剪力增量为Qi2，Q(i+1)2，计算如下

式中：Qi2为i点第二次等效剪力增量；Q(i+1)2为第i+1点第二次等效剪力增量；Vi1，V(i+1)1分别为等效剪力Q1作用下i点、i+1的水平位移增量。

将第n次等效剪力增量Q1n，Q2n，…，Qin，Q(i+1)n作用下，桩身的位移增量为V1n，V2n，…，Vin，V(i+1)n。此时竖向力Fz因变形增量产生附加弯矩，则节点i、节点i+1处的等效剪力增量Qin+1，Q(i+1)n+1计算如下

图1 杆单元受力分析示意图Fig.1 Force analysis of pole unit

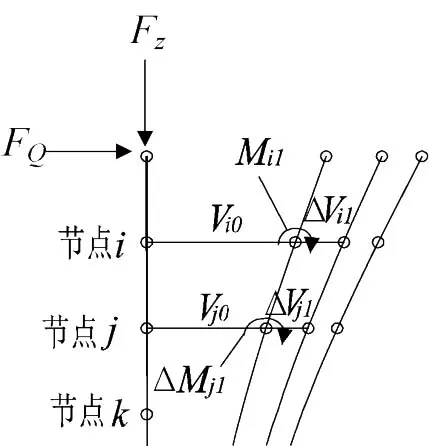
图2 基桩P-Δ效应过程模简图Fig.2 Process simulation of P-Δ effect of pile

将第二次等效剪力增量Q12，Q22，…，Qi2，Q(i+1)2记为Q2。等效剪力增Q2产生的位移增量为V2，第n次等效剪力增量Q1n，Q2n，…，Qin，Q(i+1)n记为Qn，等效剪力增量Qn产生的位移增量为Vn。则

则当n足够大时，计入P-Δ效应的基桩弯矩和位移计算如下

1.4 竖直桩等效剪力有限元迭代分析步骤

在基桩无倾斜时，倾斜荷载作用下考虑P-Δ效应的等效剪力有限元法分析步骤如下：

1划分单元并计算单元所受竖向荷载、水平荷载、单元节点对应的地基系数；计算初始荷载列阵Q0、初始刚度矩阵K、节点约束等效弹簧刚度矩阵k。2按式（3）计算基桩初始水平位移V0。3按照式（6）和式（7）计算竖向荷载因初始位移产生的等效剪力增量Q1，并按式（12）计算位移增量V1。4按式（8），重复n次，计算等效剪力增量Q2，…，Qn，按式（12）计算位移增量V2，…，Vn。5当Vn足够小，满足工程精度要求时，即停止迭代计算。6按照式（13）和式（14）计算弯矩和位移。7计算桩侧土压力。8绘制桩身内力位移图和桩侧土压力图。

设地基系数满足m法假定或(mz+C)线形增长规律，m为比例系数，z为计算分析截面至土层顶面的距离；C为地基分项系数。则土层顶面以下z处发生x水平位移对应桩侧土压力为

1.5 微倾斜桩等效剪力有限元迭代分析步骤

当基桩有略微倾斜时，则需要对初始荷载列阵F0进行修正，具体步骤如下：

1划分单元并计算单元所受竖向荷载、水平荷载、单元节点对应的地基系数；计算初始荷载列阵Q0、初始刚度矩阵K、节点约束等效弹簧刚度矩阵k。修正初始荷载列阵，即将竖向力因桩身微倾斜产生的等效剪力增量Q02直接计入初始荷载列阵，则修正后的初始荷载列阵为

2按式（5）计算基桩初始水平位移V0。3按照式（6）和式（7）计算竖向荷载因初始位移产生的附加弯矩M1，并按式（12）计算位移增量V1。 4 按式（10），重复n次，计算附加弯矩M2，…，Mn，按式（12）计算位移增量V2，…，Vn。5当Vn足够小，满足工程精度要求时，即停止停止迭代计算。6按照式（13）和式（14）计算弯矩和位移。7按式（15）计算桩侧土压力。8绘制桩身内力位移图和桩侧土压力图。

2 算例分析

2.1 竖直基桩算例分析

某桥梁基桩，冲刷线以上桩长30.212 m，其中l1=8.012 m，d1=1.8 m，E1=1.933 3×104MPa；l2=22.2 m，d2=1.8 m，E2=1.8×104MPa；冲刷线以下桩长l3=42.8 m，d3=1.8 m，E3=1.8×104MPa；地基比例系数m=10 000 kN·m-3，竖向荷载Fz=9 102.2 kN，水平荷载Fx=165 kN。按本文等效弯矩迭代有限元法自编Mat⁃lab程序计算结果和文献［7，12］结果对比如表1。

表1 不同方法计算结果比较Tab.1 Comparison of calculating results with different methods

由表1可知，本文方法计算得到的桩顶位移、地面处位移、最大弯矩及最大剪力与文献［7，12］计算结果基本一致，验证了本文方法计算竖直基桩P-Δ效应基本正确。

2.2 微倾斜基桩算例分析

基桩基本参数如2.1节所述，当桩身倾斜角θ=0.005时，文献［11］和本文计算分析结果如表2所示。

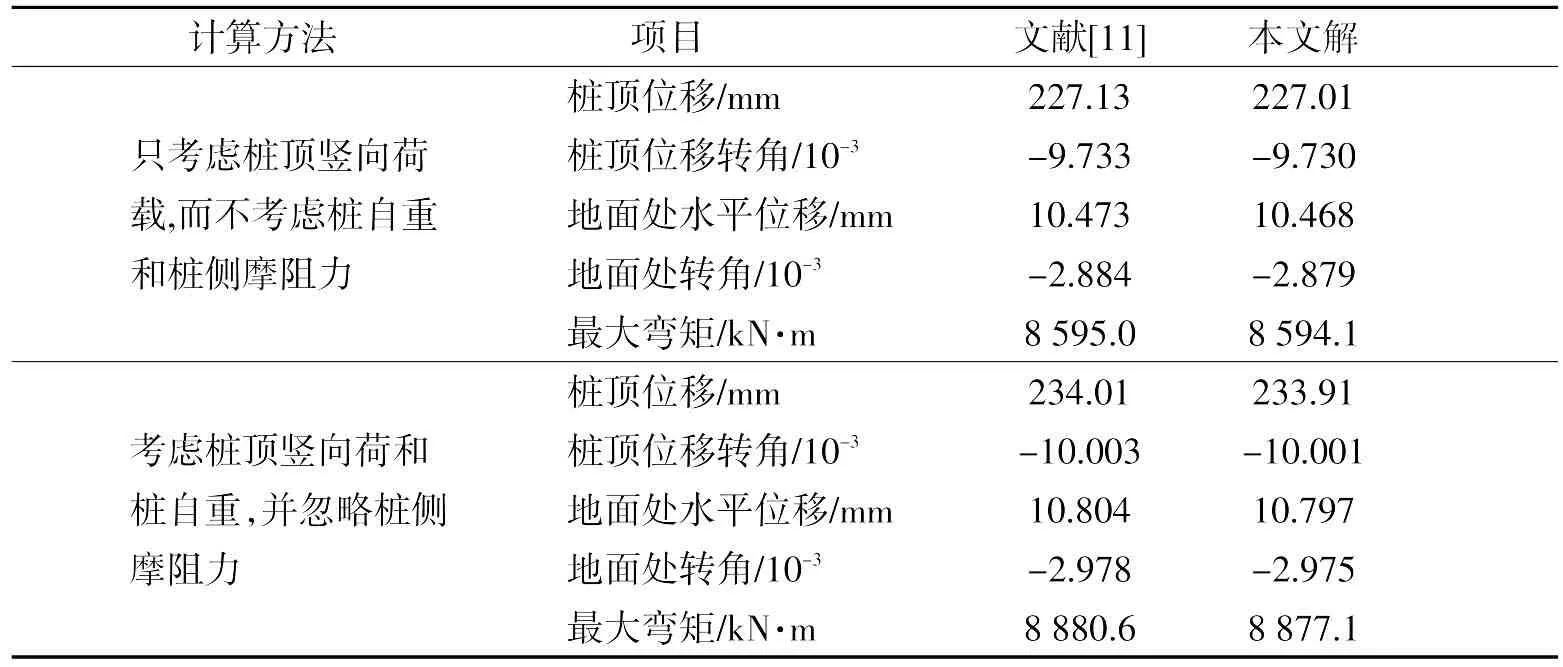
表2 不同方法计算解答比较Tab.2 Comparison of calculation with different methods

由表2可知，本文方法计算得到的桩顶位移、地面处位移、最大弯矩及最大剪力与文献［11］计算结果基本一致，验证了本文方法计算微倾斜基桩P-Δ效应基本正确。

3 结语

通过对基桩P-Δ效应产生机理研究，基于等效剪力概念，提出了等效剪力有限元迭代法，并编制了相应的有限单元Matlab分析程序，主要结论如下：

1）等效剪力有限元迭代法可用于计算竖直基桩在倾斜荷载下的P-Δ效应。

2）等效剪力有限元迭代法可用于计算微倾斜基桩在倾斜荷载下的P-Δ效应。

3）算例分析表明，当基桩地面以上较长、刚度较柔时，P-Δ效应显著，不可忽略。

［1］KISHIDA H，MEYERHOF G G.Bearing capacity of pile groups under eccentric loads in sand［J］.Proceedings of the 6thInternational Conference on soil Mechanics and Foundation Engineering ，1965，2（4）：270-273.

［2］MEYERHOF G G，MATHUR S K，VALSNAGKAR A J.The bearing capacity of rigid piles and pile groups under inclined loads in layered sand［J］.Canadian Geotechnical Journal，1981，18（4）：514-519.

［3］MEYERHOF G G，YALCINAS，MATHUR S K.Ultimate pile capacity for eccentric inclined load［J］.Journal of the geotechnical engineering division ，ASCE，1983，109（GT3）：408-423.

［4］ MEYERHOF G G，SASTRY V V R N.Bearing capacity of rigid piles under eccentric and inclined loads［J］.Canadian Geotechnical Journal，1985：22（3）：267-275.

［5］ MEYERHOF G G，GHOSH D P.Ultimate capacity of flexible piles under eccentric and inclined loads［J］.Canadian Geotechnical Journal，1989，26（1）：34-42.

［6］横山兴满（日）.桩结构物的计算方法和计算实例［M］.唐业清，吴庆荪，译.北京：人民交通出版社，1981：167-169.

［7］赵明华.轴向和横向荷载同时作用下的桩的计算［J］.湖南大学学报，1987，14（2）：68-81.

［8］赵明华，吴鸣，郭玉荣.轴横向荷载下桥梁基桩的受力分析及试验研究［J］.中国公路学报，2002，15（1）：50-54.

［9］赵明华，邬宝林，曹文贵.倾斜荷载下群桩有限元分析方法探讨［J］.中南公路工程，2003，28（2）：8-14.

［10］赵明华，邹新军，邹银生，等.倾斜荷载下基桩的改进有限元－有限层分析方法［J］.工程力学，2004，21（3）：129-13.

［11］李微哲，赵明华，单远铭，等.倾斜偏心荷载下基桩内力位移分析［J］.中南公路工程，2005，30（3）：53-57.

［12］赵明华，李微哲，曹文贵.复杂荷载及边界条件下基桩有限杆单元方法研究［J］.岩土工程学报，2006，28（9）：1059-1063.

Equivalent-shear Finite Element-iterative Method of P-Δ Effect of Pile under Inclined Loads

Li Weizhe
（Chongqing Design and Research Institute，China Coal Technology Engineering Groups，Chongqing 400016，China）

It is assumed that horizontal displacement of pile has a longitudinally cubic power function，and equivalent-shear finite element-iterative method which can analyze the P-Δ effect of piles under inclined and eccentric loads，is derived in the paper.And Matlab process of equivalent-shear finite element-iterative method is edited.Case analysis is done in the paper for displacement and stress calculation of pile under inclined and eccentric loads，moment，pile gravity，horizontal distributed loads，vertical distributed loads，scattering vertical forces and soil-pile friction.Finally conclusions are drawn as follows：equivalent-shear finite element-iterative method is proved to be an effective method for P-Δ effect analysis of piles under complex loads；P-Δ effect is notable while piers are high.

pile foundation；inclined loads；equivalent-shear finite element-iterative method；P-Δ effect

U442

A

2011-02-24

李微哲（1981－），男，硕士，研究方向为桥梁结构与基础工程计算分析研究。

1005-0523（2012）03-0031-05