基于剪枝策略的改进TDCALT算法

钟慧玲，章 梦，石永强，蔡文学

（华南理工大学经济与贸易学院，广东广州510006）

智能交通系统（intelligent transportation system，ITS）是解决交通拥挤问题的有效工具，路径规划则是其中最重要的功能之一，即给定起点和终点后，求解出一条合理的路径诱导车辆行驶.目前实现该功能的路径规划算法的基础是最短路算法，已有许多学者提出［1－3］基于固定边权的静态最短路算法，该类型算法求解的结果为一条距离最短的路径，而在现实应用中，通常需要通行时间最短（最快）的路径，求解该路径需要考虑交通状况对于通行时间的影响.受道路通行时间的不确定性和路网规模过大的双重影响，该类算法求解路径的过程效率还有待进一步提升，因此极大地限制了其实际应用（如在集中式路径诱导系统中的应用）.目前许多学者研究如何提高求解路径的算法效率［4－6］，但还存在着算法搜索盲目性等局限，故本文以提高计算效率为目标进行该类最短路算法的研究.

根据刻画道路通行时间的不同方式，考虑交通状况的最短路算法研究可以分为两类：一是将通行时间表达为时间依赖性函数的算法［4］，二是将通行时间表达为完全随机数的算法［7］.由于后者的计算效率明显低于前者，本文将基于前者进行扩展研究，即研究时间依赖性路网下的最短路算法.该类型的算法由Cooke［8］提出，后续研究主要从串行计算和并行计算两个角度来提高计算效率.串行计算应用不同加速策略提高其计算效率［9－10］：① 方向诱导策略［11］虽然能够缩小搜索空间，但是其计算效率还不能满足实际需求；② 双向搜索策略［12］执行双向搜索过程，大部分情况下能够提高计算效率，但是在最坏的情况下比单向搜索策略差，同时难以确定后向搜索的出发时刻；③ 压缩图策略［13］通过简化路网有效提高了算法效率，但是其效率还有进一步提升的空间；④ 路径分解策略［14］能够有效提升效率，但其求解的路径可能不是最短路；⑤ 分区策略［15］能够有效提高算法效率，但算法的预处理时间过长.并行计算依赖于具体的串行算法［16］，通过将串行计算并行化的方式提高计算效率，其计算效率与并行计算过程中使用的网络分割方法、串行最短路算法以及终止检测方法有较紧密的关系，是目前比较前沿的发展方向.

由于并行计算的基础是串行最短路算法，因此本文将先进行串行最短路算法的研究.针对串行计算单独使用各项加速策略存在的缺陷，目前一些研究［4，17－18］将几种不同的策略结合起来以进一步提高算法效率，比较典型的是将方向诱导策略、双向搜索策略和压缩图策略结合起来的TDCALT（time dependent core－based A＊landmarks triangle inequality）算法［4］，该算法分为两个子算法：离线预处理子算法和在线搜索子算法.首先通过离线预处理子算法对时间依赖性路网进行分层预处理以压缩路网，同时根据文献［19］进行地标点的选择处理；其次通过在线搜索子算法在经过预处理的路网上利用方向诱导策略和双向搜索策略计算最短路.该算法的效率比其他算法的效率有很大的提高［4］，但其还存在着搜索盲目性等缺陷，仍有进一步提升的空间.

本文以TDCALT算法为基础，首先对TDCALT算法中的上限值进行动态优化，提高算法效率；其次针对其搜索盲目性的缺陷（即算法搜索了明显不在最短路上的节点）通过引入应用于静态路网下最短路算法的剪枝策略［20］，将其改进为适用于时间依赖性路网的剪枝策略来弥补该缺陷，进一步提高算法效率；最后在广州市路网上通过试验对比分析本文提出的改进TDCALT算法（improved TDCALT，ITDCALT），TDCALT算法和TDIJKSTRA（time－dependent DIJKSTRA）算法在各种算法评价指标下的表现.

1 问题定义

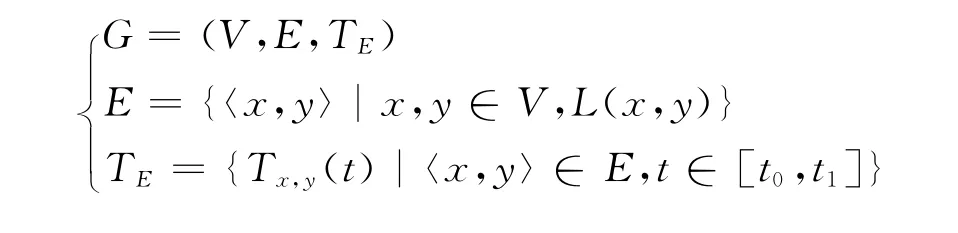
本文使用时间依赖性路网来表达路网信息和交通状况信息，时间依赖性路网G的定义如下：式中：G表示时间依赖性路网；V表示道路节点集合；E表示路段集合，其元素为有序对〈x，y〉，x为路段的起点，y为路段的终点；L（x，y）是路段〈x，y〉的长度；TE是在时间区间［t0，t1］上定义的函数，Tx，y（t）是非负实数，表示t时刻在路段〈x，y〉上的通行时间.

对于给定的起点S∈V、终点D∈V、出发时刻T，如何在G上高效地求解出在T时刻出发，从S到D的通行时间最短的路径即本文研究的主要问题.

2 ITDCALT算法

在求解时间依赖性路网的最短路算法中，TDCALT算法的效率比其他算法的效率有很大提高［4］，但是还存在着一定的缺陷，因此本文将以该算法为基础进行改进.

2.1 TDCALT算法描述

文献［4］中提出的TDCALT算法分为两个子算法：离线预处理子算法（该部分主要作用为初始化路网，只需执行一次即可）和在线搜索子算法（该部分主要作用为计算最短路，需在每一次搜索请求中执行一次）.其中离线预处理子算法应用了压缩图策略和方向诱导策略，在线搜索子算法应用了双向搜索策略和方向诱导策略.以下简要阐述两个子算法的主要步骤，为方便描述，引入以下表述：

G（V，E）：原始的时间依赖性路网；

GC（VC，EC）：经过压缩图策略处理之后的时间依赖性路网；

G（V，E）：下限值路网，即该路网中每一条路段E的通行时间都是G中该路段所有通行时间的最小值，记为len；

GC（VC，EC）：经过压缩图策略处理之后的时间依赖性下限值路网，即该路网中每一条路段EC的通行时间都是GC中该路段所有通行时间的最小值；

GCA（VCA，ECA）：经过压缩图策略和方向诱导策略处理之后的时间依赖性路网；

GCA（VCA，ECA）：经过压缩图策略和方向诱导策略处理之后的时间依赖性下限值路网，即该路网中每一条路段ECA的通行时间都是GCA中该路段所有通行时间的最小值；

GF（VF，EF）：G和GCA合并之后的路网，其中VF＝V，EF＝E∪ECA.

2.1.1 离线预处理子算法

输入：原始的时间依赖性路网G（V，E）.

输出：经过预处理的路网GCA（VCA，ECA）.

步骤：首先是基于压缩图策略的预处理子算法，其次是基于方向诱导策略的预处理子算法，分别如下：

（1）基于压缩图策略的预处理子算法

步骤1.1：对于路网G中的每一个节点v，如满足被去除的标准（如果v节点的入边数量为N，出边数量为M，对于给定的参数C，若NM＞C（N＋M），即可去除v节点［4］，其中参数C∈（0，＋∞）.不同的参数C产生不同的预处理结果，进而影响算法效率），则去除该点，同时生成虚拟边连接该点相应的前驱和后继节点，转入步骤1.2.

步骤1.2：对于每一条虚拟边，如果其连接的两个节点之间存在另一条比虚拟边更短的路径，则将虚拟边去除.如此即形成路网GC.

（2）基于方向诱导策略的预处理子算法

步骤2.1：在GC中选取N个节点作为地标点，转入步骤2.2.

步骤2.2：计算GC中每一个地标点到其他节点的通行时间和其他点到该地标点的通行时间，将这些通行时间信息存放入GC中.如此即形成路网GCA.

2.1.2 在线搜索子算法

输入：起点S，终点D，出发时刻T，路网GF，路网GCA.

输出：T时刻出发，S和D之间的最短路径P（S，D，T）及其通行时间d（S，D，T）.

步骤如下：

步骤3.1：在GF上使用TDIJKSTRA算法开始前向／后向搜索，搜索过的节点分别存入集合F／B.当搜索到v∈VCA，不再从v节点扩展搜索.当B∩F≠Ø（情况一）或者前／后向的优先级队列都为空（情况二）时，转入步骤3.2.

步骤3.2：若为情况一，在GF上以S为起点，使用TDIJKSTRA算法搜索，直到搜索到D即结束，输出P（S，D，T）以及d（S，D，T）.若为情况二，则

步骤3.2.1：以F／B中的叶节点为前向／后向搜索的优先级队列初始集合，在GCA／GCA上开始使用方向诱导策略进行搜索，且后向搜索的节点存入集合B.设双向搜索在v1点相遇，记S…v1…D的通行时间为r，转入步骤3.2.2.

步骤3.2.2：继续双向搜索，直到后向搜索中所有点的键值都超过Kr（K为给定的参数，其中参数K∈（0，1］，不同的参数K直接影响在线搜索子算法的效率以及结果路径的通行时间），则转入步骤3.2.3.

步骤3.2.3：继续前向搜索，但只搜索B中的节点，直到搜索到D即终止.输出P（S，D，T）以及d（S，D，T）.

2.2 TDCALT算法改进

TDCALT算法虽然很好地结合了多种加速策略，但还存在一定的缺陷，本文分别对其改进.

2.2.1 r值的动态更新改进

在线搜索子算法中，后向搜索的终止条件是其优先级队列中所有节点的键值全部超过Kr（步骤3.2.2），因此在保证r大于最短通行时间的前提下，r越小则后向搜索越快终止，算法的搜索空间越小，如图1所示.当r1减小为ri时，搜索空间减少的部分如深色部分所示.TDCALT算法中r被设置为双向搜索第一次相遇时所找到路径的通行时间值，如图1的r1所示.在后续的最短路搜索过程中，可能会找到更小的r值，如图1中的ri所示，但该缩小的r值信息在TDCALT算法中没有被很好利用，导致算法搜索空间大，算法效率降低.

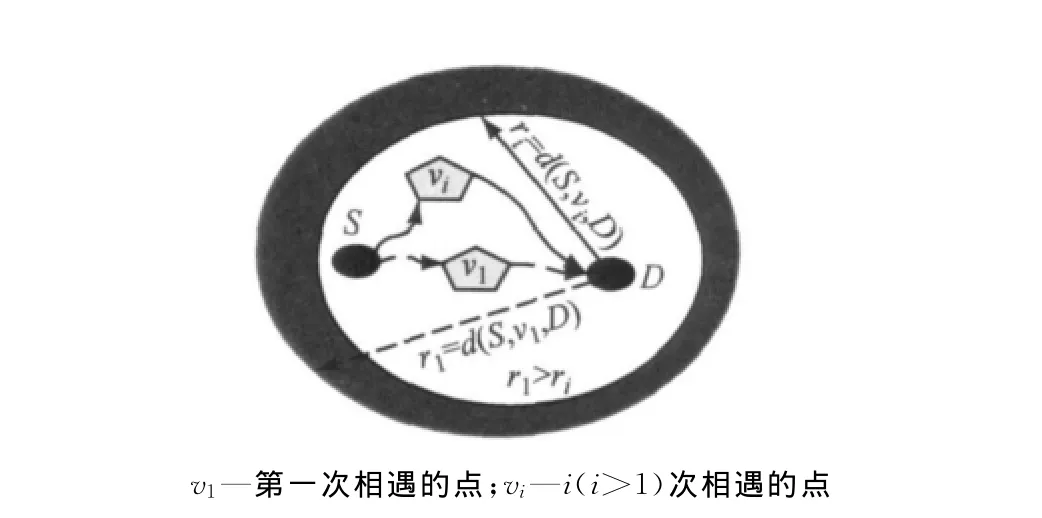
图1 不同r值的搜索空间Fig.1 Search space of different values of r

对此，本文改进为动态更新该r值.当双向搜索第一次相遇时，将r值设置为此时找到的可行路径的通行时间，如图1中的r1所示.在后续的双向搜索过程中，若找到其他可行路径的通行时间小于当前的r值，则将该r值更新为当前可行路径的通行时间值，如图1中的ri所示.如此处理既可保证r＞d（S，D，T），又可使r值不断减小，由此能够缩小搜索空间，提高算法效率.

2.2.2 剪枝策略的改进与应用

在线搜索子算法中，其搜索过程未考虑放弃搜索明显不在最短路上的节点，从而导致了搜索的盲目性，搜索空间扩大，算法效率降低.在静态最短路算法中，可以使用剪枝策略来解决该问题.该策略在静态最短路算法中能够取得很好的效果，但是不能直接应用到时间依赖性路网下的最短路算法中.本节将考虑改进剪枝策略，将其引入到时间依赖性路网下的最短路算法中，弥补TDCALT算法的缺陷.

2.2.2.1 基于Reach的静态剪枝策略

静态最短路算法中使用剪枝策略需要两个过程：离线预处理过程和在线搜索过程.在离线预处理过程中对每一节点生成一个标识信息，以标识该点是否在最短路上；在在线搜索过程中利用该标识信息判断节点是否在最短路上，以进行剪枝，避免搜索不在最短路上的节点，以此减少搜索空间，提高算法效率.文献［20］中所提出的应用于静态路网的基于Reach的剪枝策略为该类策略的典型代表.

文献［20］中对Reach的定义为：对于一条给定的最短路径P1（S…v…D），v相对于P1的Reach值P1（Reach）＝Min（d（S…v），d（v…D））.设P1，…，Pn为路网中经过v的所有的最短路，则v相对于整个路网的Reach值v.Reach＝Max（P1（Reach），P2（Reach），…，Pn（Reach））.如图2所示，P1与P2为路网中经过v的所有的最短路，P1＿Prefix为路径P1上起点到v的前半段路径，P1＿Suffix为路径P1上v到终点的后半段路径，P2＿Prefix与P2＿Suffix与前述定义类似，则P1（Reach）＝Min（d（P1＿Prefix），d（P1＿Suffix））＝7，P2（Reach）＝Min（d（P2＿Prefix），d（P2＿Suffix））＝4，v.Reach＝Max（P1（Reach），P2（Reach））＝7.文献［20］首先在离线预处理阶段计算每一个点相对整个路网的Reach值.在求解S和D之间最短路的在线搜索过程中若式（1）成立

d（S…v）＞v.Reach且d（v…D）＞v.Reach（1）则可确定v不在S和D之间的最短路上，故放弃搜索v（即剪枝操作），以减少搜索空间，提高算法效率.如图2所示，d（S…v）＝11＞v.Reach＝7且d（v…D）＝10＞v.Reach＝7，故放弃搜索v节点.

2.2.2.2 时间依赖性剪枝策略的改进

基于Reach的剪枝策略的成功应用必须满足以下两个关键条件：

条件一：离线预处理过程中，节点的Reach值必须是按照定义计算得到的值.

对于时间依赖性路网，由于其道路通行时间随时间变化，按照定义计算Reach的过程中需要确定经过v点的所有最短路，但是时间依赖性路网中不能确定上述最短路（如：P1在t1时刻是连接S和D的最短路，因为道路通行时间随时间变化，所以P1在t2时刻可能不是连接S和D的最短路），因此将不能按照定义求解Reach值，即条件一不能满足.

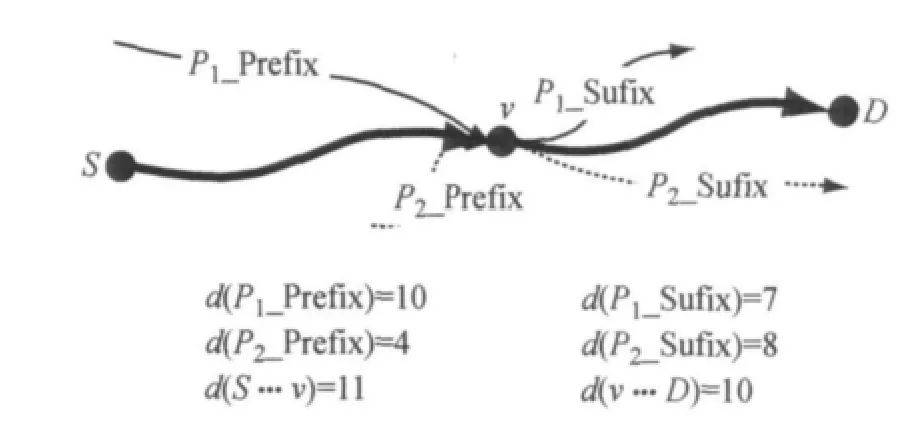
图2 基于Reach的剪枝策略示意图Fig.2 Example of Reach－based pruning strategy

条件二：在线搜索过程中，由于式（1）需要，必须能够实时获得d（S…v）和d（v…D）.

在获取d（v…D）的过程中，由于达到目的点D的时刻未知，因此d（v…D）也未知，故不能实时获取d（v…D），即条件二不能满足.

由于上述两个关键条件不能直接得到满足，因此基于Reach的剪枝策略将不能直接应用于时间依赖性路网下的最短路算法中，本文将分别针对上述两个缺陷进行改进，使其能够应用于时间依赖性路网下的最短路算法中，进一步提高算法效率.

（1）满足条件一的算法改进

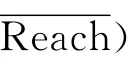
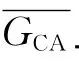
GCA为经过2.1.1节离线预处理后的路网，其通行时间为len；

Pitj为路网GCA上时刻点tj经过v节点的所有最短路（i＝1，…，n；j＝1，…，m）；

Pi为路网上经过v点的所有最短路（i＝1，…，n）.

据Reach定义，有

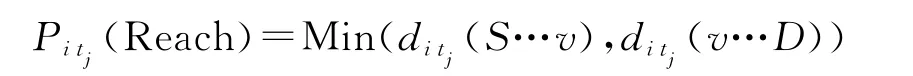
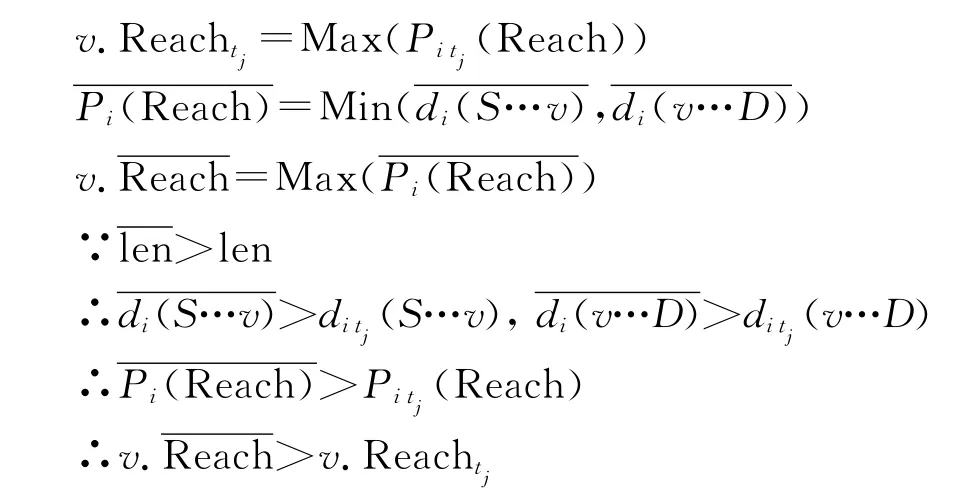
∵对于j＝1，…，m都有上述等式成立

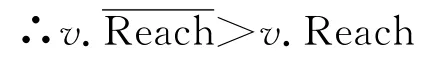
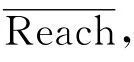
步骤如下：

（2）满足条件二的算法改进

TDCALT算法在线搜索过程中，虽然不能直接提供d（v…D）用于式（1）进行剪枝操作，但其后向搜索过程能够提供d（v…D）的下限值（d（v…D）），该值同样可以应用于式（1）进行剪枝操作，结合满足条件一的算法改进，将式（1）扩展为

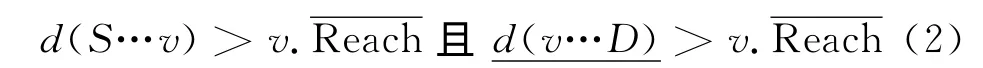
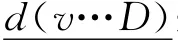
3 试验对比分析

本文从算法的效果和性能两方面选取相应的算法评价指标.为更好地展示ITDCALT算法的性能，本文以TDIJKSTRA算法作为基准算法，并在广州市路网上测试和对比分析了ITDCALT算法、TDCALT算法、TDIJKSTRA算法在不同指标下的表现.

3.1 算法评价指标

本文考虑从算法效果和算法性能两方面来评价算法.针对算法效果，本文以结果路径的通行时间作为评价指标，该指标值越小表示越接近于最短通行时间，效果越好.针对算法性能，目前多以算法的运行时间作为评价指标［4］，该指标值越小表示计算速度越快，性能越好，但该指标与计算机的性能相关程度较大.为更好地评价算法性能，本文以真实反映算法逻辑处理过程为原则，增加算法搜索空间作为评价指标.该指标完全独立于计算机性能，主要通过两个子指标来体现：① 搜索总节点数占路网总节点数比例，该指标值越小表示搜索空间越小，性能越好，下文简称指标A；② 结果路径上节点总数占搜索总点数比例，该指标值越大表示搜索空间越小，性能越好，下文简称指标B.算法评价指标体系如图3所示.

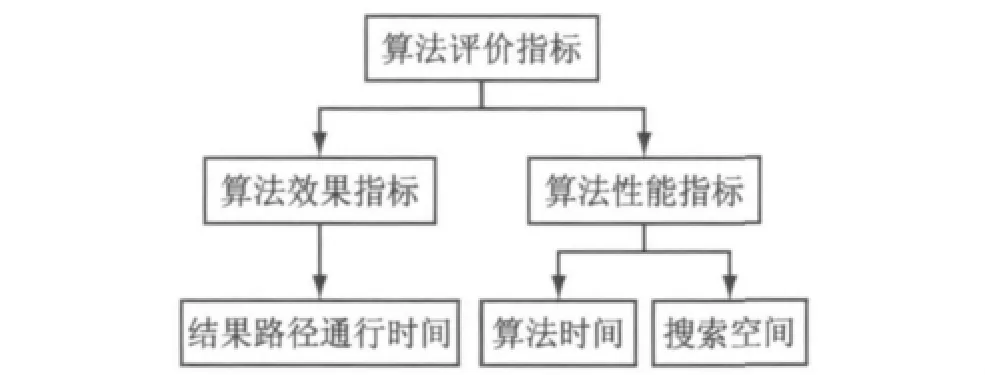
图3 算法评价指标体系Fig.3 Evaluation index of algorithm

3.2 算法测试与对比分析

本文在广州市路网上测试了ITDCALT算法、TDCALT算法、TDIJKSTRA算法的性能.该路网包含114 935条边与55 357个节点，节点的平均出入边数量为2.1，其中边信息中包含其起点、终点以及边的通行时间信息（该值为时间依赖性函数，不同时刻点道路的通行速度采用随机生成，变化范围为0～120km·h－1），点信息中包含了与之相连的出边、入边的信息.所有的算法均采用C＃（.NET 2.0）实现，算法的运行平台为Windows Server 2008，2.26GHz处理器，4G内存.

在广州市路网上随机选取了1 000对点对，每对点对分别模拟一个起点与终点，出发时刻统一为6点.分别使用ITDCALT算法、TDCALT算法、TDIJKSTRA算法，计算从6点出发，上述1 000个点对之间的最短路，并输出算法运行时间，结果路径的通行时间，搜索节点总数，结果路径上的节点总数等信息.

参数C与参数K均对算法结果有影响，但确定参数C和K的理论最优值是NP－HARD问题［2］，因此本文通过试验确定参数C和K的经验最优值.由参数C的性质可知，其不宜过大或过小，参数C过大会导致路网压缩率过小，参数C过小会导致路网压缩率过大，路网压缩率过大或过小都会降低算法效率.参数C的经验最优值受路网中节点平均出入边数量的影响，参照文献［18］中测试参数C的做法，结合测试路网中节点的平均出入边数量，本文测试了参数C从0.5到3.0，步长为0.5情况下的算法运行情况，获得经验最优的参数C为1.0.在经验最优参数C为1.0的情况下，测试了参数K从0.1到1.0，步长为0.1的情况下的算法运行情况.如表1所示，ITDCALT算法和TDCALT算法的结果路径平均通行时间与算法平均运行时间之间存在“背反”关系.随着K不断缩小，ITDCALT算法和TDCALT算法的结果路径通行时间有所延长，但延长较少，ITDCALT算法平均延长0.07%，TDCALT算法平均延长0.28%，当K＝1.0时，三种算法均输出通行时间最短的路径，同时算法运行时间也在不断缩小.设置C＝1.0，K＝1.0，三种算法在算法运行时间和搜索空间上的性能表现如表2，3所示.

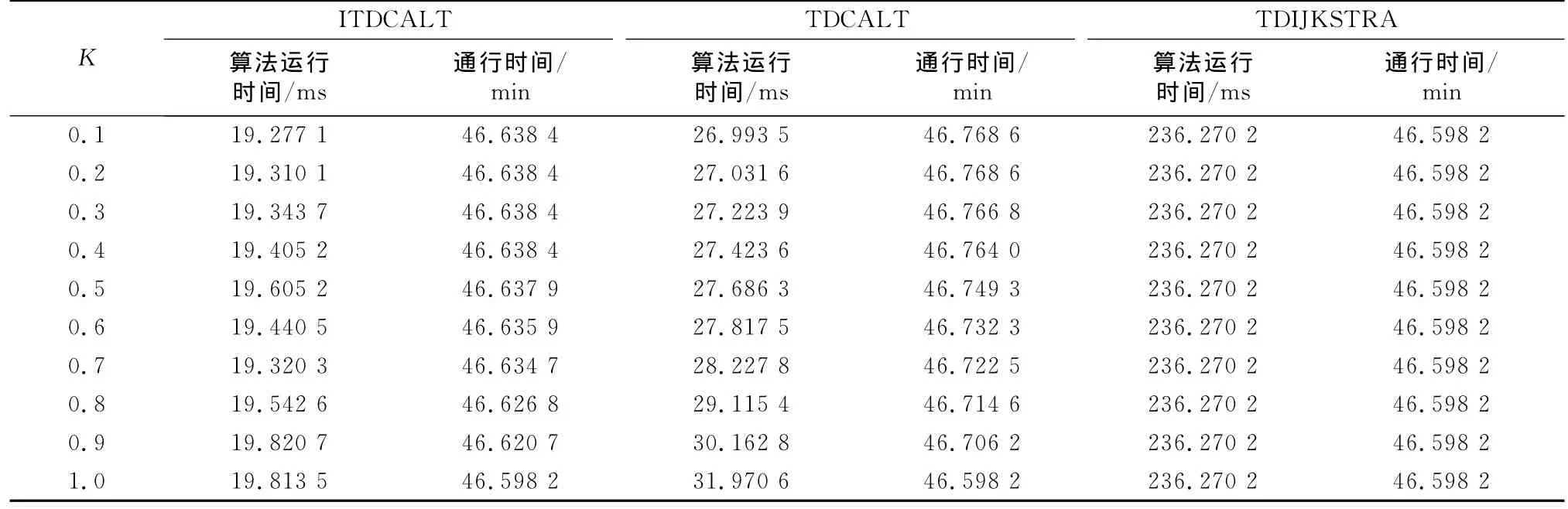
表1 不同参数K的算法运行时间与通行时间Tab.1 Running time and travel time of algorithm when Kis different

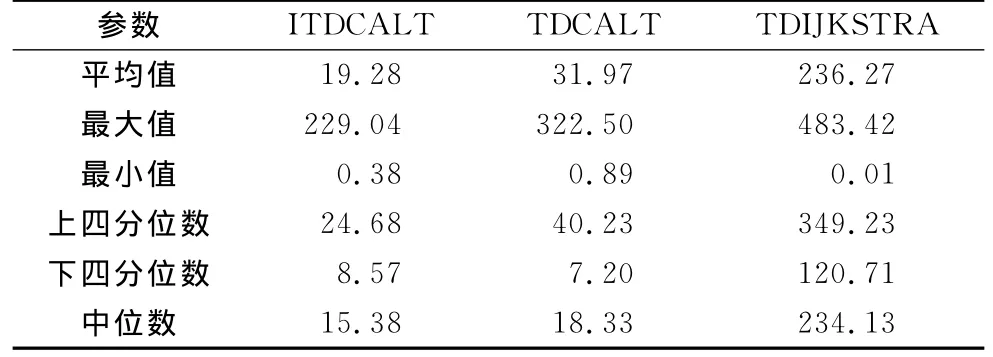
表2 算法运行时间表Tab.2 Running time of algorithms ms

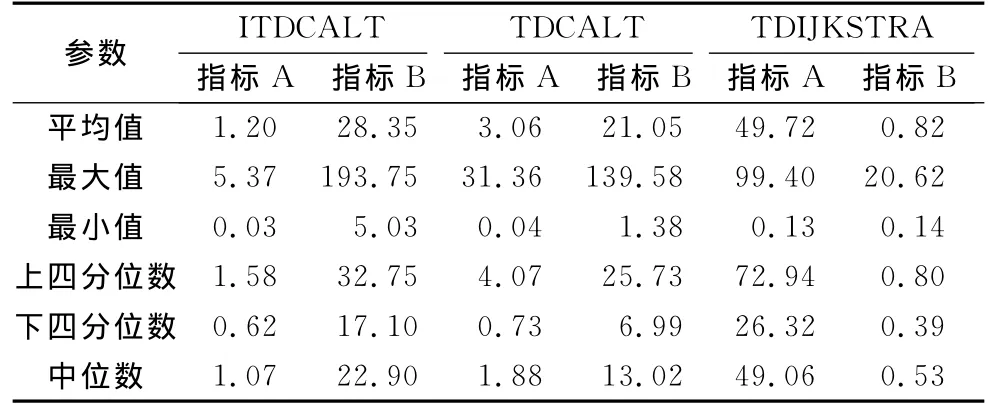
表3 算法搜索空间Tab.3 Search space of algorithms %

通过上述试验结果的分析，可以得到以下结论：

（1）ITDCALT算法的性能最高，且最为稳定.①由表2可知，ITDCALT算法的平均运行时间最少，平均仅需19.28ms，仅为TDCALT算法的61.97%及TDIJKSTRA算法的8.39%.②由表3可知，ITDCALT算法的搜索空间最小.从指标A的平均值上看，ITDCALT算法的平均值是最低的，仅为1.20%，而TDCALT算法的该指标值为3.06%，约为ITDCALT算法的2.55倍，TDIJKSTRA算法的该指标为49.72%，约为ITDCALT算法的41.43倍.从指标B的平均值上看，ITDCALT算法的指标值为28.35%，而TDCALT算法的该指标的平均值为21.05%，TDIJKSTRA算法的该指标平均值为0.82%.ITDCALT算法的指标B值与TDCALT算法的指标B值相似，主要原因为ITDCALT算法的搜索节点数较TDCALT算法少，导致其在指标B上优势性不明显.③ 表2，3中四分位数的分布表明ITDCALT算法的运行时间与搜索空间比TDCALT和TDIJKSTRA算法更为稳定.

4 结语

本文针对大规模交通网络中求解最短路的低效性与非实时性问题，构造了一种融合交通状况信息的高效最短路算法.该算法通过时间依赖性路网刻画路网信息和交通状况信息，通过改进目前效率较高的TDCALT算法，结合改进的剪枝策略来提高最短路算法的效率.试验表明，本文所提出的算法在算法运行时间和搜索空间两个指标上都明显优于原算法.在智能交通系统的集中式路径诱导系统中，该优势不仅能够提高系统的响应速度，同时能降低算法占用的计算机资源.该研究成果目前已得到了初步试用，取得了较好的效果.未来可以考虑：① 采用不同的时间依赖性函数来刻画交通状况信息，更好地拟合真实交通状况；② 考虑本算法的并行计算研究，进一步提高效率.

［1］ Sommer C.Approximate shortest path and distance queries in networks［D］.Tokyo：The University of Tokyo，2010.

［2］ Bauer R，Columbus T，Katz B，et al.Preprocessing speed－up techniques is hard［C］／／Algorithms and Complexity.Rome：Springer Verlag，2010：359－370.

［3］ Sanders P，Schultes D.Highway hierarchies hasten exact shortest path queries［C］／／13th European Symposium on Algorithms.Palma de Mallorca：Springer Verlag，2005：568－579.

［4］ Delling D，Nannicini G.Bidirectional core－based routing in dynamic time－dependent road networks［C］／／Proceedings of 19th International Symposium on Algorithms and Computation.Gold Coast：Springer Verlag，2008：813－824.

［5］ Sherali H D，Hobeika A G，Kangwalklai S，et al.Timedependent，label－constrained shortest path problems with applications［J］.Transportation Science，2003，37（3）：278.

［6］ Sherali H D，Jeenanunta C，Hobeika A G.The approachdependent，time－dependent，label－constrained shortest path problem［J］.Networks，2006，48（2）：56.

［7］ Demetrescu C，Italiano G F.Algorithmic techniques for maintaining shortest routes in dynamic networks［J］.Electronic Notes in Theoretical Computer Science，2007，171（1）：3.

［8］ Cooke K L.The shortest route through a network with timedependent internodal transit times［J］.Journal of Mathematical Analysis and Application，1966，14（3）：493.

［9］ Buriol L S，Resende M G C，Thorup M.Speeding up dynamic shortest－path algorithms［J］.Journal on Computing，2008，20（2）：191.

［10］ Hamacher H W，Ruzika S，Tjandra S A.Algorithms for timedependent bicriteria shortest path problems［J］.Discrete Optimization，2006，3（3）：238.

［11］ Nannicini G.Bidirectional A＊search for time dependent fast path［C］／／Proceedings of the 7th Workshop on Experimental Algorithms.New York：Springer Verlag，2008：334－346.

［12］ Wan－Yen L，Zwicker M.Bidirectional search for interactive motion synthesis［J］.Computer Graphics Forum，2010，29（2）：563.

［13］ Delling D，Nannicini G.Core routing on dynamic timedependent road network［J］.Journal on Computing，2012，24（2）：187.

［14］ Fua L，Sunb D，Rilett L R.Heuristic shortest path algorithms for transportation applications：state of the art［J］.Computers＆Operations Research，2006，33：3324.

［15］ Nannicini G，Baptiste P，Krob D，et al.Fast computation of point－point paths on time－dependent road networks［C］／／Proceedings of the 2nd International Conference on Combinatorial Optimization and Applications.Newfoundland：Springer Verlag，2008：225－234.

［16］ 倪安宁，隽志才，高林杰.交通网络最短路径并行算法研究综述［J］.公路交通科技，2006，23（12）：128.

NI Anning，JUAN Zhicai，GAO Linjie.An overview of research on parallel shortest path algorithm in transportation network［J］.Journal of Highway and Transportation Research and Development，2006，23（12）：128.

［17］ Muhring R，Schilling H，Schutz B，et al.Partitioning graph to speed up DIJKSTRA’s algorithm［J］.Journal of Experimental Algorithmics，2007，11（28）：1.

［18］ Delling D.Time－dependent SHARC－routing［J］.Algorithmica，2011，60（1）：60.

［19］ Goldberg A V，Harrelson C.Computing the shortest path：A＊search meets graph theory［C］／／Proceedings of the Sixteenth Annual ACM－SIAM Symposium on Discrete Algorithms.Vancouver BC：Society for Industrial and Applied Mathematics，2005：156－165.

［20］ Gutman R.Reach－based routing：a new approach to shortest path algorithms optimized for road networks［C］／／Proceedings of 6th Workshop on Algorithm Engineering and Experiments.Berlin：Springer Verlag，2004：332－343.