极大似然法在飞机起飞性能参数辨识中的应用

于雪梅，程伟，谷伟岩

(1.北京航空航天大学航空科学与工程学院，北京 100191;2.中航通用飞机有限责任公司试飞交付中心，广东珠海 519015)

引言

飞行器气动参数辨识自 Warner和 Norton［1］的早期工作以来，已经有九十多年的历史。以往飞行器气动参数的确定是通过理论计算和风洞试验进行的，而理论计算有其局限性，风洞试验与实际飞行条件也存在差异，两者所得到的气动特性均难以准确反应实际飞行特性。因此，飞行试验是确定飞机飞行性能最有效的方法，应尽可能在飞行试验的基础上确定飞机在使用范围内的飞行性能，但这样不可避免地存在耗资大、周期长的问题。

随着计算机和数值计算技术的发展，系统辨识理论在飞行器设计和研制过程中的作用越来越大，尤其是经过20世纪60年代后期以来的研究，飞机气动参数辨识已发展成为一个较为独立的系统辨识分支［2］。极大似然法是参数辨识领域中常用的一种方法，理论上已经证明参数的极大似然估计是一致渐进、有效、无偏的估计，且具有良好的收敛性［3-4］，因而该方法在飞行器参数估计中得到广泛应用。目前，世界发达国家对飞机状态估计和参数辨识的研究已发展到实用水平［5-6］。我国学者在飞行器的飞行试验参数识别方面也进行了许多研究，但总体来说，大部分研究都集中于操纵特性的气动导数和模态特性研究上［7-8］，对于飞行性能的气动参数识别和总体特性研究并不多见。

本文结合Y12飞机双发起飞飞行试验实测数据，研究了利用极大似然法进行飞机起飞性能参数辨识的问题，建立了Y12飞机起飞性能的数学模型，并从简化灵敏度导数计算角度提出了以飞机在起飞滑跑过程中速度增量为观测量的观测方程［9］，分析给出待辨识参数和利用极大似然法进行起飞参数辨识的方法，采用Matlab软件进行了系统仿真［10］，并针对主要辨识影响因素变化对结果的影响进行了讨论。

极大似然法与以前关于飞机起飞性能的数据处理方法相比具有较高的处理效率和辨识精度，因此，将极大似然法应用于飞机起飞性能参数辨识具有一定的现实意义，既可提高工作效率，又可节约试验成本。

1 飞机起飞性能建模

起飞性能涉及的内容包括:全部发动机工作正常起飞、一台发动机失效继续起飞、一台发动机失效中断起飞。本文仅研究利用极大似然法对全发起飞地面滑跑起飞性能的辨识。

1.1 起飞性能数学模型

从动力学角度分析，在不考虑跑道坡度的情况下，飞机在滑跑过程中承受的力有:飞机重力(G)、发动机推力(P)、气动阻力(D)、地面摩擦力(Ff)、地面对机轮的支持力(N)、机翼升力L。飞机起飞滑跑段的运动方程可简化为［10］:

式中，CL，CD分别为飞机起飞构型状态下(襟翼在起飞位置、起落架放下等)对应于停机迎角的升力系数、阻力系数;f为地面滑跑摩擦系数;ρ为大气密度;SW为机翼面积。一般情况下，发动机推力P是飞行速度、高度的函数，由发动机厂家提供。

飞机在滑跑过程中各力随飞行速度的变化如图1所示。图中，Q为总阻力;VLOF为离地真速。在起飞离地点处有:V=VLOF，L=G。

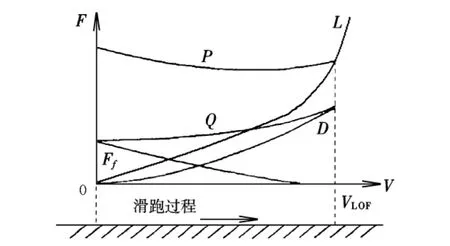
图1 起飞滑跑过程中各力随速度的变化曲线

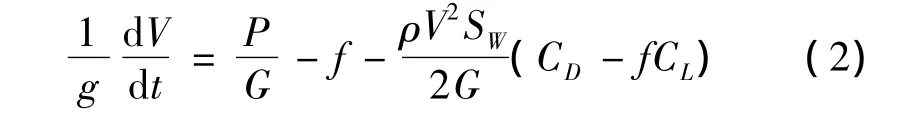
式(1)和式(2)中的速度均为飞行真速(VT)。因为飞机升力、阻力的大小只与真速有关，而起飞滑跑距离的大小却与地速(VG)有关，因此需考虑风对起飞距离的影响。真速和地速的关系为VG=VT±VW(逆风取“－”，顺风取“+”)。起飞滑跑距离可表达为d S=VGd t，积分则可获得起飞地面滑跑距离为:

将各参数的表达式带入式(1)，并除以G，有:

式中，CL，LOF为离地瞬间的升力系数。

由式(3)可见，影响起飞滑跑距离的主要因素有:起飞质量、襟翼状态、跑道条件(粗糙度、场压)、外界大气环境(场温、风速风向)等。起飞滑跑距离表达式中有3个未知参数(CD，CL，f)，如取综合阻力系数 A=(CD－fCL)，则待辨参数变为 f，A。

1.2 起飞性能辨识模型及辨识方法

根据极大似然法的辨识原理，在进行参数辨识前，首先需要选择观测量并给出观测方程［3］。如将式(3)作为观测方程，将L视为观测量，则待辨识参数f和A值位于分母中，计算中发现，此时灵敏度导数不易计算。因此，分析后选择起飞滑跑过程的速度增量为观测量，以简化观测方程，便于进行灵敏度导数计算和参数辨识。

将起飞滑跑过程分为足够多的小段，每一小段均可视为匀加速过程，则由式(3)可得速度增量为:

由式(8)可见，代价函数相当于测量量和观测量的累计差值，根据模型要求，其值可以适当变化。一般计算时，当|Jj+1－Jj|/|Jj|＜ε(迭代精度)时停止迭代，亦可事先定义代价函数或迭代次数进行迭代并检查收敛情况。

2 起飞性能飞行试验及数据采集

起飞性能飞行试验测试的目的就是通过准确测量飞机在起飞过程中的滑跑距离、速度、姿态、发动机功率等参数的变化规律来确定起飞性能。Y12飞机起飞性能的测试参数包括:飞机起飞质量、起飞襟翼偏度、大气温度、机场场压高度、风速、风向、指示空速、水平滑跑距离、发动机功率(包括螺旋桨转速和扭矩)、起飞松刹车信号、前轮离地信号等。以Y12飞机双发起飞性能为例，某一状态(起飞质量5 300 kg，起飞襟翼0°，大气温度 －14℃，机场高度145 m，逆风风速0.5 m/s)的指示空速、高度、发动机扭矩测试结果如图2所示(由于篇幅限制，其它参数未绘出)。

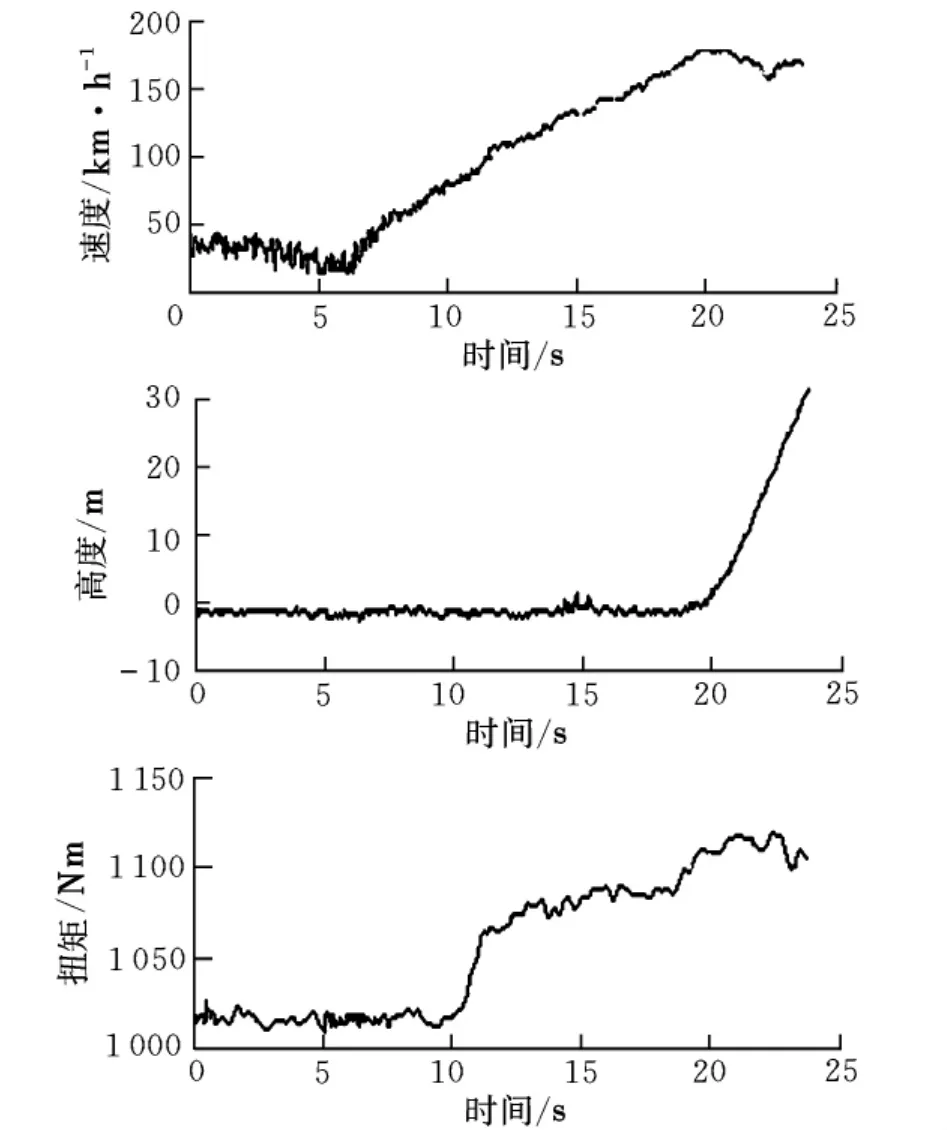
图2 飞机起飞测试结果

以上仅给出一组测试数据，实际辨识过程中采用取多组测试数据进行，将辨识结果取平均值作为这一状态飞行的待辨参数值。

3 极大似然法参数辨识

采用Matlab软件进行编程，具体辨识步骤如下:

(1)对机载测试数据(图2)进行预处理(主要包括滤波、中值、曲线拟合)，并将校正空速转换成真速，选取合适辨识数据段，建立测试结果数据文件。

(2)根据试验状态、飞机参数和发动机参数，计算对应试验状态的发动机推力和大气密度。

(3)根据待辨识参数的理论计算结果和工作经验，选取待辨识参数的迭代初值。对于Y12飞机，在起飞地面滑跑过程中，有关参数的取值范围为:

地面滑跑摩擦系数:f=0.03～0.04

机翼面积:SW=34.27 m2

阻力系数:CD=0.16～0.20

升力系数:CL=1.2～1.4

计算得综合阻力系数:A=4.1～5.2

因此，在迭代初始，两个待辨识参数f和A的初值应在上述范围内取值。

(4)将飞行速度随时间的变化转换为速度增量随时间的变化并作为观测量，建立数据文件。

(5)选择样本长度N=100。

(6)合理选择代价函数和迭代精度或迭代次数，按极大似然法计算待辨参数的灵敏度导数和代价函数，进行迭代计算。最终使辨识参数经过有限次数的迭代后，收敛于一个合理、可信的结果。在本文的参数辨识过程中，经过比较，选用了人工控制迭代次数的方法。

经上述步骤，得到辨识结果如表1所示。

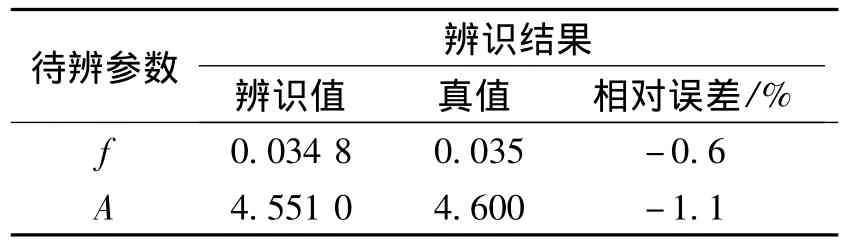
表1 起飞参数辨识结果

真值是Y12飞机经过多年飞行试验确定的结果，比较真实可信。从表中可见:辨识结果与真值的相对误差约为1%。将试验时飞机的状态参数、飞行参数和辨识值/真值分别代入式(3)中进行计算，可得到起飞滑跑距离的扩展结果分别为407 m，419 m，从工程应用角度看，该辨识结果能够满足性能试飞精度要求。

辨识参数迭代结果如图3所示。

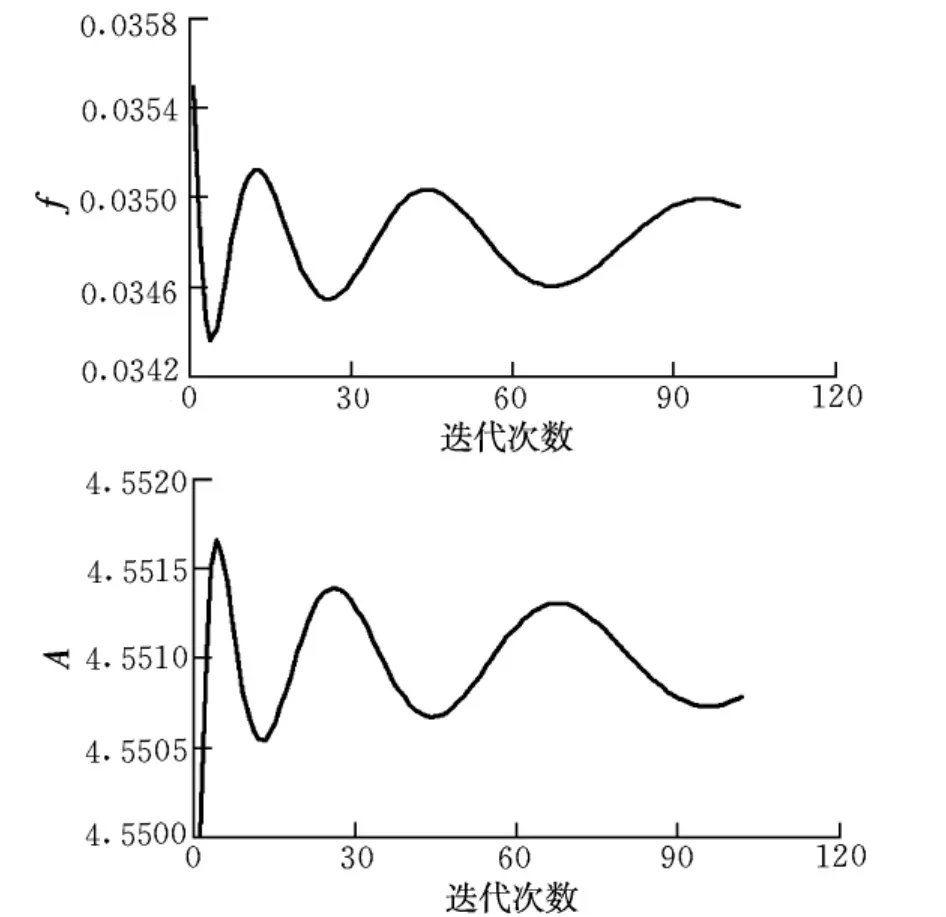
图3 辨识参数迭代结果曲线(J=0.01)

由图3可见，经过30次的迭代后，辨识参数已基本趋于稳定。迭代过程的变化趋势说明了迭代的收敛性。由于迭代曲线纵坐标的取值范围很小，因此，曲线在迭代到30次后虽然看似有一定的波动，但其实际变化范围已经很小，可以认为曲线收敛。

4 辨识结果影响因素分析

4.1 迭代初值影响

将地面滑跑摩擦系数f和综合阻力系数A的迭代初值分别有意识地放大和缩小，采用同样的数据处理和辨识方法进行辨识。结果表明，经过40次左右的迭代后，迭代参数的波动范围已趋正常范围，因此，本文采用的方法对迭代初值偏差具有良好的适应性。

4.2 代价函数影响

分别采用J=0.05，J=0.01和J=0.005三种代价函数进行对比计算，结果表明:代价函数越小，迭代次数越多，但迭代结果并没有显著提高，f基本在0.034 6～0.035 0之间波动，波动幅度为1%，A基本在4.550 5～4.551 3之间波动，波动幅度小于0.1%。因此，选择合适的代价函数可以经过较少次数的迭代就可以获得满意的结果。

4.3 迭代次数影响

分别采用50，100和500三种迭代次数进行计算，结果表明:迭代次数增多对迭代结果没有显著影响。因此，在进行参数辨识时，应选择合适的迭代次数，可以通过较少次数的迭代获得满意的结果。

4.4 敏感参数影响

在进行测试数据参数辨识初期，对测试数据进行预处理后，参数辨识结果很不理想，辨识结果在一个较大的范围内波动，有时还出现发散现象。

经过对观测方程式(5)的分析发现，对Y12飞机的状态参数和试验数据而言，方程式(5)中的ΔV和C0两项为同一量级，C1θ1项比ΔV低一个量级，而C2θ2U项则低至少两个量级。在开始进行实测数据参数辨识时，观测量ΔV的有效位数取值到10－1，这样，其它参数的变化就被ΔV的取值误差吃掉了。因此，观测量ΔV和C0的精度对辨识结果具有重要影响。结果表明，将观测量ΔV和C0的有效位数取到10－3，参数辨识结果明显改善。

因此，观测方程中各个参数对辨识结果的影响作用是不一样的。在参数辨识前，应初步对观测方程中的各个参数进行敏感性分析，以保证测试数据的选取有足够的精度。

4.5 试验数据段的选取

对Y12飞机起飞性能测试而言，由于速度传感器有效工作范围的限制(小速度指示误差较大)，起飞滑跑段速度的有效范围基本在50 km/h以上，从该速度到飞机起飞离地，对应的时间历程约为10 s左右。测试系统的采样率较高(通常50～100 Hz)，虽然理论上选取任意几秒作为数据段测试数据点都足以进行参数辨识，但实际上数据段的选取对辨识结果有一定影响，应当有目的地选取测试数据段。

从观测方程式(5)可见，式中C2θ2U项比观测量ΔV低一个量级甚至更多，而U为起飞滑跑速度的平方，因此，为使C2θ2U项与观测量ΔV项具有更接近的量级，试验数据段应尽量在较大速度范围内选取。

4.6 样本长度影响分析

极大似然法在理论上希望样本长度越大越好，然而实际样本过长不仅会增加计算量，而且数据中非理想误差的增加也会影响参数辨识结果。为确定样本长度对辨识结果的影响，本文进行了不同样本长度的对比辨识，在同样的测试数据段内，分别进行样本长度N=100和N=500情况的迭代，迭代结果表明:对Y12飞机起飞性能进行辨识，在同样迭代次数的情况下，样本长度的增加并没有使迭代收敛增快，在样本长度N=100的情况下，已具有比较满意的辨识结果，当样本长度N=500时，辨识结果精度并没有显著提高，而迭代计算需要的时间却显著增加。

5 结束语

本文研究了利用极大似然法进行飞机起飞性能飞行试验数据参数辨识的问题，确立了辨识模型和待辨参数，采用Matlab软件进行计算，结果表明极大似然法可以快速、准确地辨识出起飞性能所需的参数，并具有较高的精度。从工程实用的角度出发，辨识中所使用的观测方程应具有简单的形式，以便于灵敏度导数的计算。在观测方程中，各参数对辨识结果的影响是不一样的，为保证辨识结果的准确性，应进行敏感参数分析，确保测试数据的记录具有足够的精度。另外，代价函数、迭代次数、样本长度、数据段的选取等对参数辨识结果精度都可能有影响，在参数辨识过程中应注意分析，以尽可能经过较少迭代获得最优结果。与传统方法相比，极大似然法具有数据处理效率高、辨识结果精度高的特点，在今后的飞机起飞性能数据分析中应进一步推广，并应探索将其应用到其它性能分析中的方法。

［1］ Warner E P，Norton F H.Preliminary report on free flight test［R］.NASA Report No 70，1919.

［2］ 蔡金狮.飞行器系统辨识学［M］.北京:国防工业出版社，2002:287-294.

［3］ 叶建华.过程辨识技术［M］.上海:上海大学出版社，2007:59-82.

［4］ 王志贤.最优状态估计与系统辨识［M］.西安:西北工业大学出版社，2004:223-243.

［5］ Klein V，Mogan DR.Estimation ofbias errors inmeasured airplane responses using maximum likelihood method［R］.NASA TM-89059，1987:79-82.

［6］ Maine R E.Programmer’smanual for MMLE3，a general FORTRAN program formaximum likelihood parameter estimation［R］.NASA TP-1690，1981.

［7］ 全昌业.气动参数辨识飞机飞行试验研究回顾［J］.飞行试验，1999，15(2):8-14.

［8］ 刘兴堂，万少松.一种估计飞行器运动特性的实用极大似然法［J］.飞行力学，1999，17(3):65-70.

［9］ 谷伟岩.运十二飞机起飞性能参数辨识研究［D］.北京:北京航空航天大学，2000.

［10］ 张静.Matlab在控制系统中的应用［M］.北京:电子工业出版社，2008:364-83.