灰色层次分析法在建筑工程评标中的应用

朱雪芹，张 文

（华北水利水电学院，河南 郑州 450011）

建设部《房屋建筑和市政基础设施工程施工招标投标管理办法》第四十一条规定：“评标可以采用综合评估法、经评审的最低投标价法或者法律法规允许的其他评标方法”．目前，综合评估法是在招标、评标中使用较广泛的一种方法，采用这种方法时，需要招标人确定各项评价指标及其权重系数．确定权重系数的方法有很多，最常用的是层次分析法［1－5］．但在传统的层次分析法中，忽视了人对信息认知的灰色性［6］．所谓认知的灰色性是指人的认知能力是有限的，个人无法接受系统提供的所有决策信息，从而使决策问题成为了“部分信息已知，部分信息未知”的灰色问题．因此在构造判断矩阵时，人们只能确定各因素的取值范围，而不能确定其完全属于某一个标度，这个范围可以用区间灰数表示．为了解决这个问题，笔者采用灰色层次分析法确定各评标标准的系数，根据评标系数选择最优投标人，以保证工程的高质、高效．

1 灰色层次分析法

灰色层次分析法是将区间灰数的白化处理方法与已有的层次分析法结合起来［6］，是对传统层次分析法的改进，具体有以下5个步骤．

步骤1 建立递阶层次结构．根据对问题的分析，把所包含的因素按照最高层、中间层和最低层的形式排列起来，并用结构图的形式表示层次的递阶结构和各因素之间的从属关系．

步骤2 确定判断灰矩阵．邀请m位专家，利用德尔菲法对每一层各个元素的相对重要性给出客观的判断，并分别构造m个判断灰矩阵 R（k）），R（k））为灰正互反阵［7］．

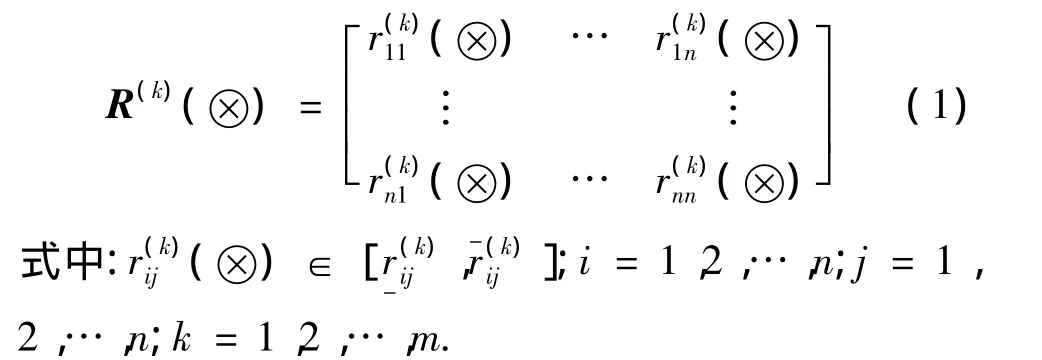
再以各位专家的判断灰矩阵及各位专家的权重ηk构造判断灰矩阵R（），R（）为灰正互反阵，根据公式

步骤3 对判断灰矩阵进行白化处理［8］，白化值为

其中：αij∈［0，1］;αij=1 － αji;

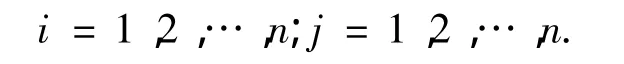
求得以定位系数为αij的白化矩阵为

步骤4 计算各准则下元素的相对权重及一致性检验．计算判断矩阵（）的最大特征值λmax和经过归一化的特征向量W［1］．特征向量即为指标权重，且满足（）W= λmaxW，主特征值

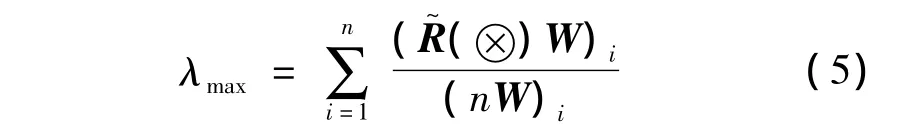
对判断矩阵的一致性进行检验，需要计算它的一致性指标C．I．和平均随机一致性指标R．I．，

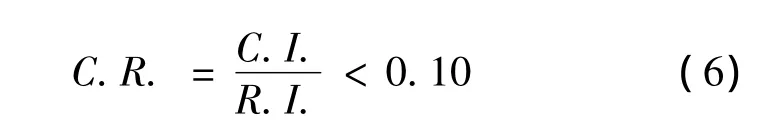
步骤5 计算综合权重的一致性检验．计算针对上一层次来说本层次所有元素重要性的权值，即各层元素的综合权重，并检验总排序是否具有满意的一致性．假设上一层次B中各元素的权重值分别为 β1，β2，…，βn，则本层次 C 的一致性指标及平均随机一致性指标分别为

式中：C．I．i为与βi对应的C层次中判断矩阵的一致性指标;R．I．i为与βi对应的C层次中判断矩阵的随机一致性指标．当满足式（6）时，本层次的判断矩阵满足一致性．

2 应用实例

某项目进行施工招标，在招标文件中确定了各项评标指标，现根据招标文件的要求确定各项指标的权重，从而确定最佳投标方案［9］．

步骤1 根据招标文件中建立的科学合理的评价指标，建立递阶层次结构模型，详见表1．

表1 招标项目评标指标表

步骤2 招标企业组织有关方面的评标专家，利用德尔菲法，按照表1所示的层次结构，由各位专家给出各层次的判断灰矩阵．由于各位专家所掌握的信息不完全，所以并不能确定各因素间的重要程度完全属于某一个标度，只能根据已有的决策信息确定一个标度的区间，用区间灰数表示．然后再根据各位专家的专业水平给定权重ηk，根据公式（2）求得准则层的总判断灰矩阵R1）以及措施层的总判断灰矩阵R2（），R3（），R4）和R5），分别如下．

步骤3 对上述各层的总判断灰矩阵进行白化处理．在进行系统分析过程中，通常以灰数的白化值代替灰数来进行系统分析，当区间灰数取值的分布信息缺乏时，通常采用等权均值白化［6］．所以在该实例中，取定位系数αij=0．5，得到各层的白化矩阵，并计算白化矩阵的最大特征值λmax及特征向量Wi，Wi（i=1，2，3，4，5）的分量即为各元素单排序的权重，最后检验判断矩阵的一致性．

由公式（5）和公式（6）计算可得：

由计算结果可知，上述判断矩阵具有满意的一致性，所得的特征向量即指标权重是可以被接受的．

步骤4 计算综合权重 ω1，ω2，ω3，ω4．措施层的综合权重由W1与Wj（j=2，3，4，5）综合确定．

式中：ω1，ω2，ω3，ω4中的数值分别表示为质量、工期、投标报价和社会信誉准则下各指标的权重系数．

步骤5 检验总排序的一致性．由式（7）和（8）得到C．I．=0．016，R．I．=1．011，C．R．=0．016＜0．10，总排序一致性检验通过．

步骤6 根据以上结果，选定最佳投标方案及最佳投标人．由各评标专家根据招标文件要求，对各投标方案评比并给出在质量、工期、投标报价和社会信誉准则下的评价指标的分值，综合各评标专家给出的分数取其平均值．

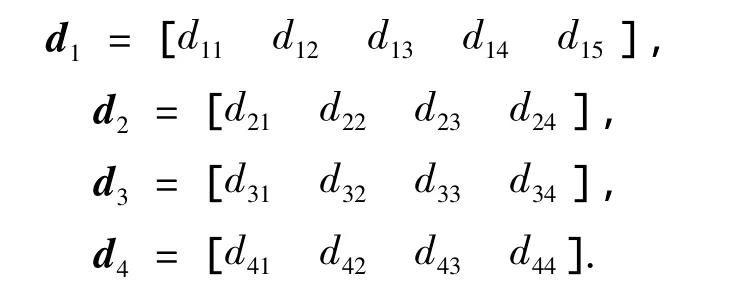
3 结语

应用实例表明，把灰色理论与层次分析法有机结合的灰色层次分析法应用到建筑工程评标中确实是行之有效的，这种方法能够有效地把人对信息认识的灰色性充分地考虑进去，在一定程度上克服了层次分析法在分析问题中的不足．在建筑工程项目评标中运用该方法能够更准确地对评价指标赋予权重，从而提高评标定标的准确性及合理性，使建设单位能够更加科学合理地选择最优投标人，保证工程项目的顺利实施．同时，由于该方法较为简单，并且具有较强的操作性及现实意义，所以也便于在实际应用中得到推广．但是在应用中也要注意，招标文件中所建立的评标指标体系不能做到完全细致准确，需充分反映业主的偏好与倾向以及评委的主观认识对评标结果的影响等客观事实的存在．

［1］杜纲．管理数学基础理论与应用［M］．修订版．天津：天津大学出版社，2003．

［2］邹坦，陈慧．基于可拓层次分析法的建设工程评标［J］．科技广场，2010（8）：199－201．

［3］靖凤伟，杨永国，窦贤明．用层次分析法选择电力最佳修复方案［J］．华北水利水电学院学报，2010，31（3）：48－51．

［4］高崇，李澎，王征．基于灰色关联分析法的边坡稳定性分析［J］．华北水利水电学院学报，2010，31（3）：111－114．

［5］徐建新，刘宏利，李彦彬．闸坝生态调度效果多层次模糊综合评价［J］．华北水利水电学院学报，2012，33（1）：15－18．

［6］谢乃明，刘思峰．灰色层次分析法及其定位求解［J］．江南大学学报，2004，3（1）：87 －89．

［7］周春堂．灰色层次分析法及其应用［J］．工程数学，1998，14（2）：44 －48．

［8］刘思峰，党耀国，方志耕，等．灰色系统理论及其应用［M］．5 版．北京：科学出版社，2010．

［9］何增勤．工程项目投标策略［M］．天津：天津大学出版社，2004．