可用度约束条件下装备健康管理信息测试周期优化研究

杨述明，邱静，刘冠军，杨鹏

(国防科学技术大学 机电工程与自动化学院，湖南 长沙410073)

0 引言

装备健康管理系统利用测试信息，结合各种模型和算法来监控、诊断、预测和评估装备健康水平，并结合各种可用资源触发最佳维修决策［1-3］。装备健康管理系统对于提高装备安全性、可靠性、维修性和经济可承受性，降低全寿命周期费用，实现自主维修、预知维修具有重要意义［4-5］。健康管理的观念、体系与内涵的研究首先始于美国军方，然后逐步扩展到民用工业领域。从公开发表的资料看，健康管理系统应用遍及航空、航天、汽车、桥梁、重型机械、工业工程、半导体制造、核电站、大型水坝等领域。在航天器中进行健康管理工程验证的项目有X-33、X-34、X-37、DS-1 等，军用飞机有F/A-18、F-22、F-35、UCAV 等，此外在民用飞机(如波音777 飞机)等其他国民经济部门也在开展应用研究。国外健康管理系统的两种典型代表是NASA、波音、霍尼韦尔等研究单位提出的运载器综合健康管理(IVHM)［6］和洛克希德·马丁公司在F-35 项目中提出的预测与健康管理(PHM)［7］。国内对于健康管理的研究刚刚起步，国防科学技术大学、北京航空航天大学、北京理工大学、西北工业大学、哈尔滨工业大学、军械工程学院、民用航空学院等单位进行了现代意义上的健康管理技术的跟踪和概念研究。

目前国内外对健康管理的研究主要集中在体系、方法和模型等方面，很少关注其前端的信息感知与测试。然而，信息感知与测试是实现健康管理的前提和基础［8-9］。因此，何时对装备进行测试显得十分重要，测试周期过长，不能及时发现装备的故障征兆会使得装备经常处于故障状态，影响可用度;测试周期太短，测试成本增加。在类似问题的研究中主要考虑单一优化目标，比如费用［10］、可用度［11］，没有全面衡量各种要素。然而对于武器装备尤其是航空航天系统如导弹、战机和雷达等，可用度是非常重要的约束［12］。本文在装备退化模型和控制限维修策略的基础上，考虑装备的可用度约束，以测试周期为决策变量，以费用率为优化目标进行最优测试周期设计，更符合装备的实际情况。

1 健康退化模型与控制限维修策略

对于贮存模式装备，通过实施定期测试确定装备健康状态，在依据状态进行维修决策。因此，应首先描述装备健康状态退化过程和基于健康状态的维修策略。

装备在贮存过程中，由于自身内部元器件的老化和外部环境的影响，其健康状态会随时间逐渐退化，其过程本质是一个随机过程，因此使用随机过程进行退化建模符合客观实际［13］。针对连续退化的随机模型应用较广，其中最为典型的是广义路径模型［10］和Gamma 过程模型［14］。广义路径模型非常适合描述总体的退化行为，而Gamma 过程模型对于单调劣化的随机过程建模具有特别的优势。连续劣化模型虽然能够比较准确地刻画系统的客观劣化过程，但是状态的连续性大大增加了建模和分析的难度。尽管装备退化失效是连续变化的过程，但忽略局部变化之间的微小差异，总可以将其用有限状态的Markov 过程刻画［15］。

设装备的健康状态空间为S ={0，1，…，s}，在装备正常退化过程中，记任意时刻t 装备的健康状态为随机变量X(t)，则{X(t)，t≥0}为S 上的时间连续状态离散Markov 过程，其状态演化及转移如图1所示。

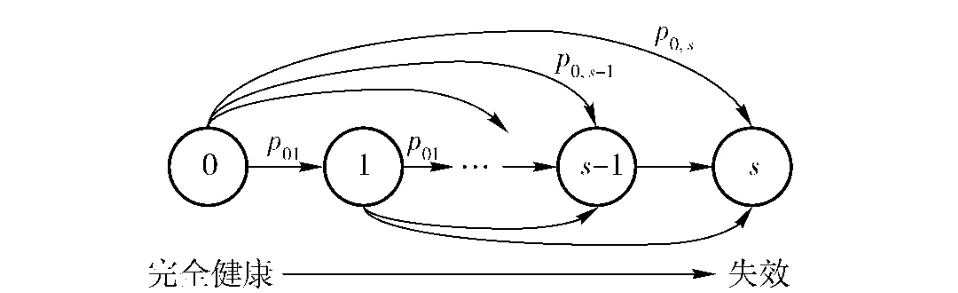
图1 装备健康退化模型Fig.1 Equipment health degradation model

装备从状态0 开始，随着时间流逝，健康水平逐渐退化直到故障状态s.对于∀i，j，l∈S，t∈［0，+∞)相关定义为:转移概率函数p(t)ij(h)=Pr{X(h +t)=j|X(h)=i}，初始概率分布ql=Pr{X(0)=l}，绝对概率分布q(t)i=Pr{X(t)=i}.显然，装备的退化Markov 过程满足如下性质:1)Pr{X(0)=0}=1;2)若j ＜i，则pij=0;3)若0 ≤t1＜t2，则X(t1)＜X(t2);4)状态s 是最小闭集，称为吸收态。

在健康状态退化模型描述基础上，控制限维修策略(CLMP)［17］可以表述为:通过测试获取的状态信息评估装备的健康水平，当X(t)＜r 时，不采取任何措施;当r ≤X(t)＜s 时，采取预防性维修;当X(t)=s 时，采取修复性维修。状态r 和s 称为预防性维修和修复性维修阈值。

装备一般分为贮存模式和使用模式，对于贮存模式下的装备一般采取周期测试(测试周期设为τ)，并且装备的健康状态只能通过测试获知，包括装备处于失效状态的情况。基于装备退化模型和CLMP 的健康管理流程如图2所示。

2 周期测试决策模型

2.1 模型假设

1)本文主要研究贮存模式下装备的周期测试策略;

2)对装备的行为包括:测试、预防性维修和修复性维修，且测试和维修均是完美的;

图2 装备健康管理流程Fig.2 Equipment health management process

3)从初始工作状态出发，到维修重新回到该状态构成一个更新周期T，更新周期内周期测试的次数为随机变量ε，进行预防性维修和修复性维修的概率分别为PP和PR;

4)测试时间为tT个时间单位，费用为cT个费用单位;预防性维修时间为tP个时间单位，费用为cP个费用单位;修复性维修时间为tR个时间单位，费用为cR个费用单位。且通常满足:tT＜tP＜tR，cT＜cP＜cR。由于装备的失效状态也需要测试确定，因此可能出现维修延迟的情况，维修延迟时间为随机变量Y;

5)装备的可用度要求下限为A0.

2.2 决策目标

在优化测试周期时，决策目标一般包括费用率、可用度。由更新过程定理［16］知，长期运行的平均费用率、可用度可以看成一个更新周期内的平均费用率和可用度。

由假设条件可知更新周期内的平均费用为E［C(T)］=cTE(ε)+cPPP+tRPR，更新周期平均长度为因此更新周期内平均费用率为

装备的可使用率是衡量装备具有一定战斗力，应付各种突发事件的能力，通常可用使用可用度表示。使用可用度通常定义为装备可用时间与总任务时间之比，受装备可靠性、维修性、测试性和保障性的影响非常大，是一个综合性指标。在更新周期T内的使用可用度可以表示为

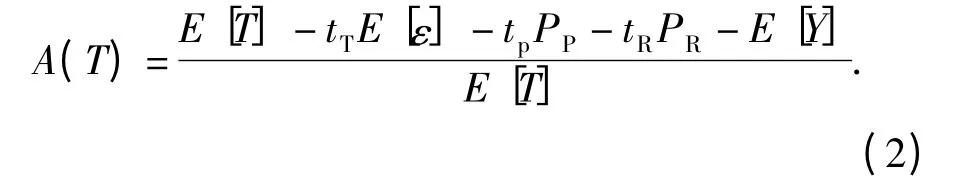
2.3 权衡优化模型

对于武器装备尤其是航空航天装备如导弹、火箭、飞机等，装备可用度是必须考虑的，建模应该是多目标优化问题。在实际中，装备费用率和可用度往往无法同时达到最优，通常做法是使某主目标最优，同时把其他目标看成约束。本文以可用度为约束，以测试周期τ 为决策变量，以费用率为优化目标建立权衡优化模型

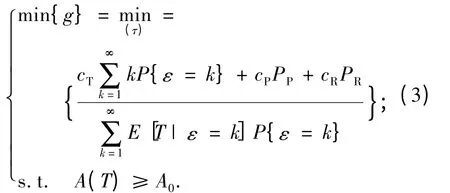
下面利用前面的退化模型和CLMP 确定方程中的具体表达式。更新分别由预防性维修和修复性维修引起时:

在进行第k 次测试时进行预防性维修和修复性维修的概率分别为

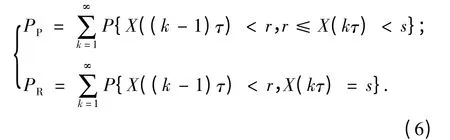
维修延迟平均时间［17］可以表示为

现在关键是确定P{X((k -1)τ)＜r，r≤X(kτ)＜s}和P{X((k-1)τ)＜r，X(kτ)=s}的具体表达式。根据Markov 退化过程，到时间t 时没有到达状态j 的概率为

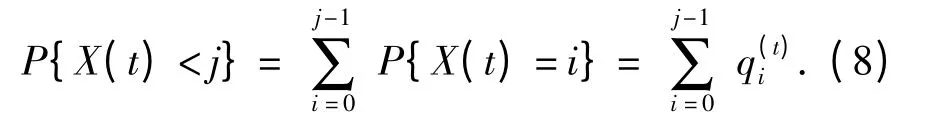
结合前面转移概率函数、初始概率分布和绝对概率分布的定义，以及全概率和条件概率公式，可以得到

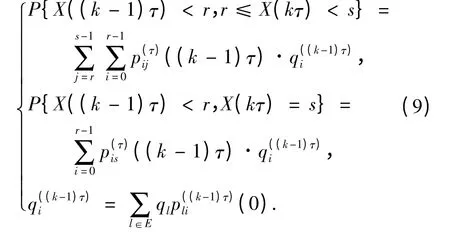
对于齐次马尔可夫过程，转移概率函数与状态的起始时刻无关，只与转移时间有关，即p(t)ij(h)=pij(t)则(9)式变为

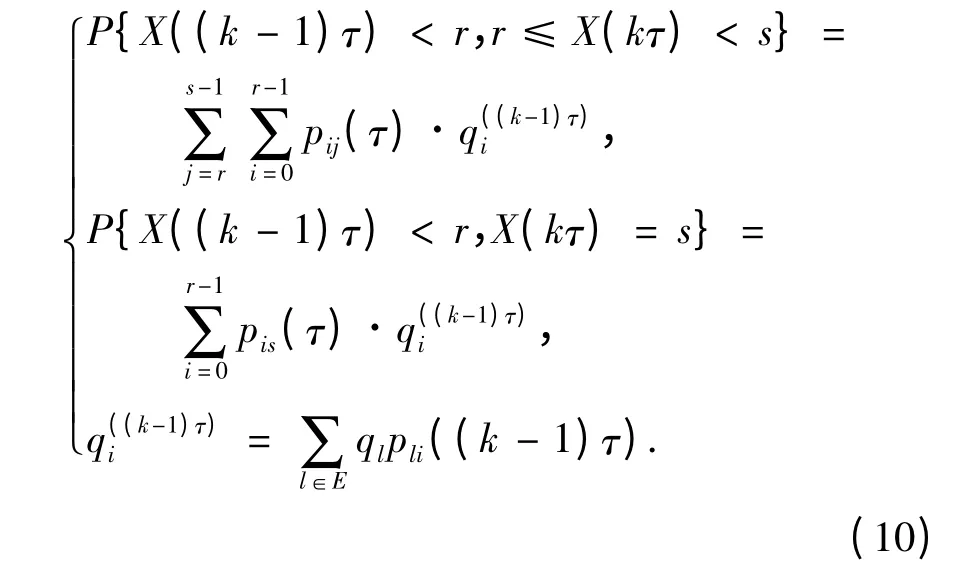
通常称{pij(τ)}是{pij(t)，t≥0}步长为τ 的离散骨架，它对应某一Markov 链的一步转移概率。因此，只要知道了装备退化Markov 过程的初始概率分布和一步转移概率，就可以确定权衡优化模型的具体解析式。

3 案例分析

以某型导弹为对象进行验证研究，该导弹的健康状态离散成7 个状态，即状态空间为S ={0，1，2，3，4，5，6}，导弹以概率1 处于完好状态，即初始概率分布为ql=［1，0，0，0，0，0，0］，r =3，s =6.装备退化Markov 模型为状态独立、齐次Markov 过程，状态转移率为0.05.若设cT=0.1，cP=1，cR=3，tT=2，tP=5，tR=10.要求贮存期间可用度不低于0.9.通过遗传算法进行优化求解，设置种群数量50 个，遗传代数取200 代，交叉率为0.5，变异率为0.05，通过计算获得无约束和有约束下的最优测试周期如图3和图4所示。

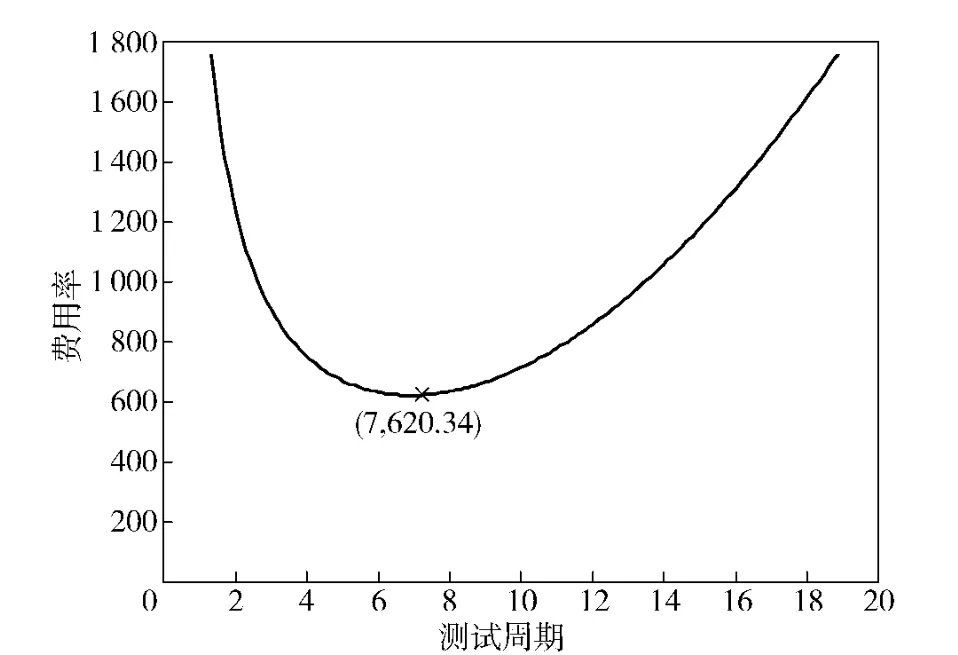
图3 无约束下测试周期与费用率关系Fig.3 Cost per unit time trend varying with test periodicity under no constraints

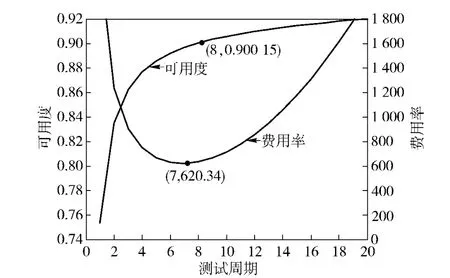
图4 测试周期与可用度关系Fig.4 Relationship between test periodicity and availability

由图3可以看出，在无约束下，存在一个最优测试周期，使得费用率最小，即当测试周期约为7 时，费用率最小为620.34.由图4可以分析:由于装备的可用度约束A0≥0.90，当测试周期为8 时，可用度为0.900 15，满足可用度要求，再结合费用率与测试周期的关系，可以得到可用度约束下的最优测试周期约为8，对应的费用率约为632.92.

4 结论

本文提出了可用度约束条件下的测试周期优化模型，并基于更新过程实现的测试周期优化设计。仿真结果显示，可用度约束直接影响测试周期，基于可用度约束的测试周期更具合理性和指导性。所提模型对于指导BIT 功能欠缺且需要外部周期性检测的长贮装备具有一定的指导意义。在应用中，也可以根据具体要求，以可用度为优化目标进行测试周期优化设计。

References)

［1］ Cheng S，Azarian M，Pecht M.Sensor systems for prognostics and health management［J］.Sensors，2010，10(4):5774 -5797.

［2］ Lau D，Fong B.Special issue on prognostics and health management［J］.Microelectronics Reliability，2011，51(2):253 -254.

［3］ Julka N，Thirunavukkarasu A，Lendermann P，et al.Making use of prognostics healthmanagement information for aerospace spare components logistics network optimization［J］.Computers in Industry，2011，62(6):613 -622.

［4］ Pecht M G.Prognostics and health management of electronics［M］.New Jersey:John Wiley ＆ Sons Inc，2008.

［5］ Orsagh R F，Brown D W，Kalgren P W，et al.Prognostic health management for avionic systems［C］∥IEEE Aerospace Conference.Montana:IEEE，2006:1 -7.

［6］ Paris D E，Trevino L C，Watson M D.A framework for integration of IVHM technologies for intelligent integration for vehicle management［C］∥IEEE Aerospace Conference.Montana:IEEE，2005:3843 -3852.

［7］ Hess A，Fila L.The joint strike fighter (JSF)PHM concept:potential impact on aging aircraft problems［C］∥IEEE Aerospace Conference Proceedings.Montana:IEEE，2002:3021 -3026.

［8］ Cheng S，Tom K，Thomas L，Pecht M.A wireless sensor system for prognostics［J］.IEEE Sensors Journal，2010，10(4):856-862.

［9］ Zhang G F.Optimum sensor localization/selection in a diagnostic/prognostic architecture［D］.Georgia:Georgia Institute of Technology，2005.

［10］ Jiang R.Optimization of alarm threshold and sequential inspection scheme［J］.Reliability Engineering ＆ System Safety，2010，95(3):208 -215.

［11］ 谭林，陈童，郭波.基于几何过程的单部件可修系统最优维修策略［J］.系统工程，2008，26(6):88 -92.TAN Lin，CHEN Tong，GUO Bo.Optimal maintenance strategy for the repairable system consisting of one component based on geometric process［J］.System Engineering，2008，26(6):88 -92.(in Chinese)

［12］ Nakagawa T，Mizutani S，Chen M.A summary of periodic and random inspection policies［J］.Reliability Engineering ＆ System Safety，2010，95(8):906 -911.

［13］ 赵建印.基于性能退化数据的可靠性建模与应用研究［D］.长沙:国防科学技术大学，2005.ZHAO Jian-yin.Study on reliability modeling and application based on performance degradation data［D］.Changsha:National University of Defense Technology，2005.(in Chinese)

［14］ Van Noortwijk J M.A survey of the application of gamma processes in maintenance［J］.Reliability Engineering ＆ System Safety，2009，94(1):2 -21.

［15］ Tseng S T，Peng C Y.Stochastic diffusion modeling of degradation data［J］.Journal of Data Science，2007，5:315 -333.

［16］ 陆大金.随机过程及其应用［M］.北京:清华大学出版社，2003.LU Da-jin.Stochastic process and its application［M］.Beijing:Tsinghua University Press，2003.(in Chinese)

［17］ Kallen M J，Van Noortwijk J M.Optimal periodic inspection of a deterioration process with sequential condition states［J］.International Journal of Pressure Vessels and Piping，2006，83(4):249-255.