光学遥感图像变量分裂迭代快速复原算法

宋义刚，肖亮，韦志辉，2，黄丽丽

(1.南京理工大学 计算机科学与技术学院，江苏 南京210094;2.南京理工大学 应用数学系，江苏 南京210094)

0 引言

光学遥感成像是对地观测和深空探测的重要数据获取途径。然而成像过程中光学系统散焦、运动和大气扰动等造成的模糊效应以及成像系统光电因素引起的噪声干扰等严重影响了图像的视觉质量和空间分辨率。如何去除模糊效应和抑制噪声干扰是光学遥感图像复原需要解决的问题，也是光学遥感图像超分辨的关键技术［1］。

目前图像复原算法可分为频域算法和空间域算法。Wiener 滤波算法简单、便于实现、在噪声水平不大的情形能够获得较好的复原效果，但随着噪声水平增大复原效果急剧下降并存在较多的“寄生波纹效应”;约束最小二乘算法具有Wiener 滤波类似的频域公式，能够减少“寄生波纹效应”但是不能很好的保持图像的边缘［2］。文献［3］基于Contourlet变换的遥感图像去噪新算法，为遥感图像噪声抑制提供了新的手段。文献［4］研究提出了一种基于超分辨图像处理的模糊图像盲复原算法，其利用推定复原图像的拉普拉斯算子获得参数的估计，算法用于遥感图像复原取得较好的效果。文献［5］提出将多准则优化理论引入到光学层析成像图像重建取得很好的结果，对光学遥感图像复原也具有指导意义。

光学遥感图像复原是一个病态重建问题，为克服重建过程的病态性，人们提出基于正则化和偏微分方程的图像复原方法，如文献［7－8］提出基于各向异性扩散方程的图像滤波算法，文献［9］针对航天湍流降质图像给出极大似然估计正则化复原算法。Rudin－Osher 提出了图像去噪的全变差(TV)图像模型［10］。TV 模型将图像建模为有界变差空间(BV 空间)的函数，能够很好保持图像的边缘结构，成为广为认可的图像复原和超分辨领域的图像正则化模型［10－14］。但是基于TV 模型的复原算法还存在一些问题，包括:复原图像会存在“阶梯效应”;如果采取最速下降法求解，算法的收敛速度较低，经实验表明需要迭代上百次才能达到收敛，并且每次迭代的复杂度非常高，降低了该算法的实用性。最近一些学者提出了一些快速算法，例如:针对TV 去噪模型的快速投影算法［11］，多重网格算法［12］，基于引入辅助变量的代价函数方法［13］等。

本文给出了一种新的变量分裂快速迭代快速复原算法。首先通过引入待去模糊图像的辅助变量、图像梯度的辅助变量，构造逼近于原始TV 复原模型的代理代价函数。通过分析代理代价函数特殊结构，充分利用循环周期卷积核与图像的卷积等价于傅里叶域的乘积，并且由傅里叶变换不会改变欧式范数的性质，设计了三阶段解析迭代算法。算法具有如下优点:1)迭代过程每个阶段均是具有解析解的子问题求解，并且每次迭代仅需2 次快速傅里叶变换和1 次快速逆傅里叶变换，算法的时间复杂度仅为O(M2logM)，其中M2为图像像素个数。2)迭代过程考虑了人眼对图像平坦区域和边缘区域噪声的感知特性，通过估计迭代系统中自适应的正则化参数，改善了图像复原的效果，一定程度上克服了“阶梯效应”。

1 已有全变差正则化复原算法与问题分析

1.1 光学遥感成像降质模型

下面讨论一般遥感成像系统的降质模型。记F(h)为点扩散函数h 的傅里叶变换，并令(ξ，η)∈为频域坐标，遥感成像光学系统的调制传递函数(MTF)一般包含如下3 部分:

1)感光耦合器件(CCD)的调制传递函数。在焦平面上CCD 敏感像素是一个细小的［－ c/2，c/2］2窗口，其中c 为相邻CCD 像元的距离，可以用一个矩形函数来描述，这样可推导出CCD 的MTF为

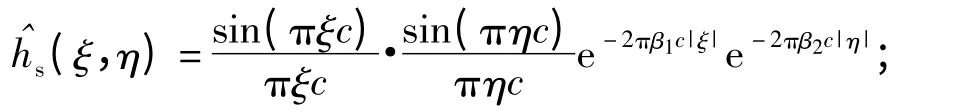
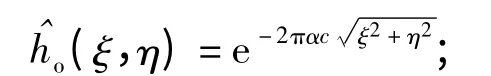
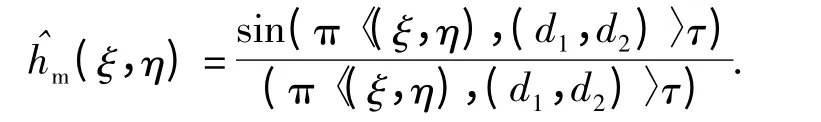
可假设遥感成像光学系统为圆对称系统，则总体MTF 是各部分MTF 的乘积:

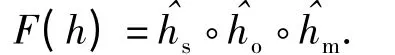
假设u(x，y)为未降质的图像，从而降质观测图像u0(x，y)为

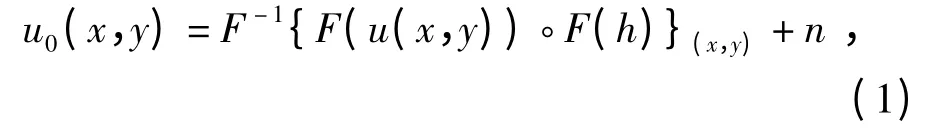
或 u0(x，y)=u(x，y)⊗h(x，y)+n，

式中:(x，y)为空间坐标;(u，v)为频率域坐标;F 和F－1分别表示傅里叶正反变换;n 表示噪声;⊗表示卷积算子。

1.2 基本模型与问题分析

图像复原实质上从u0中估计合适的u，属于Hardmard 意义下非适定数学反问题。基于Rudin－Osher 连续全变差模型，人们提出了图像正则化复原算法［11－13］，

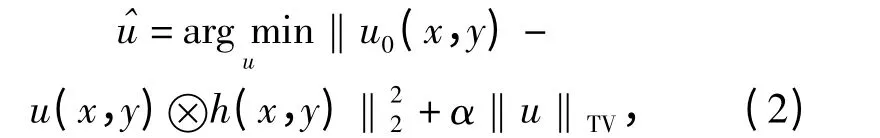
式中:参数α 为正的拉格朗日乘子，连续全变差模型定义为

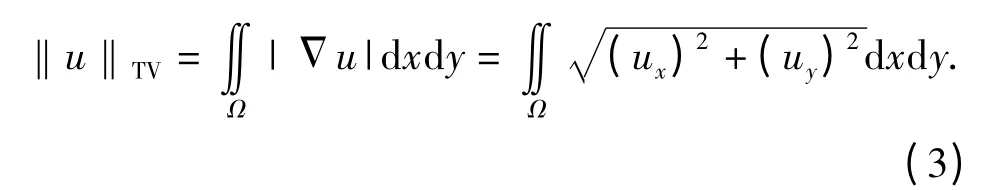
利用变分法和梯度下降法(GD)转换为求解非线性方程［10］:

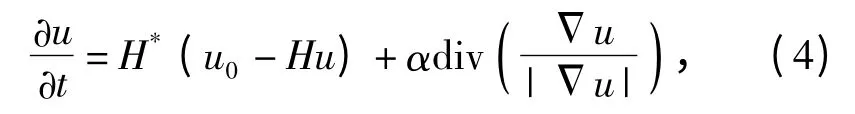
式中:H 为h 对应的卷积算子，为避免|u| =0，需引入参数ε ＞0，将其替换为全变差图像复原模型能够减少“寄生波纹效应”也能较好保持图像边缘，但是会导致图像中出现“阶梯效应”。

另外虽然梯度下降法是目前求解非线性变分问题最直观、最常用且实现比较简单的算法，但算法存在如下缺点:1)收敛速度较慢;2)在求解过程中需引入参数ε ＞0，且因为参数ε 的引入迭代解不能严格收敛于(6)式的精确解;3)每次迭代都要计算一次H*H，由于线性空间不变的模糊算子的支集一般很大，当受到模糊影响的遥感图像尺寸很大时去模糊的计算代价更高。文献［13］针对该问题，通过引入辅助变量w 和w 与u 的惩罚项，构造逼近于模型(2)式的代理代价函数，

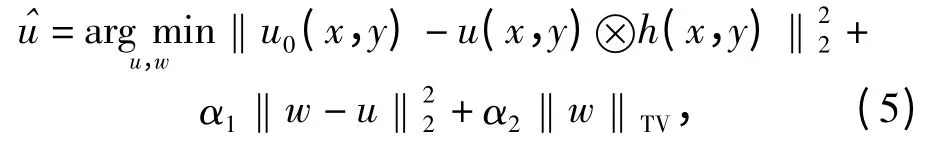
显然当参数α1足够大时，能够逼近于模型(2)式，并可采取交错迭代法求解:

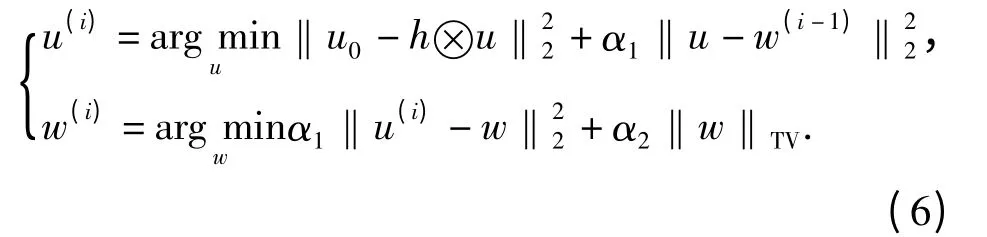
其好处是将原始TV 复原转化为去模糊和TV去噪2 个子问题。而去模糊是二次凸泛函的最优，可通过共扼梯度法快速求解;而TV 去噪可采取Chambolle 快速投影算法。从而避免了每次迭代都要计算一次H*H，且Chambolle 投影算法是TV 去噪的精确求解算法，实验结果表明该算法收敛速度提高一个数量级。该算法对TV 去噪引起的“阶梯效应”仍没有很好解决。

2 代理函数模型与快速优化算法

2.1 代理函数模型建立

本文在离散化框架下建立基于全变差的代理代价函数图像复原模型。不失一般性，考虑M ×M 大小的离散观测图像u0∈RM2，理想图像u∈RM2和噪声n∈RM2.光学系统的点扩散函数为h，则降质模型为

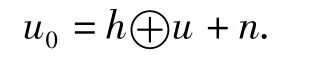
定义离散梯度算子D∶RM2→RM2为

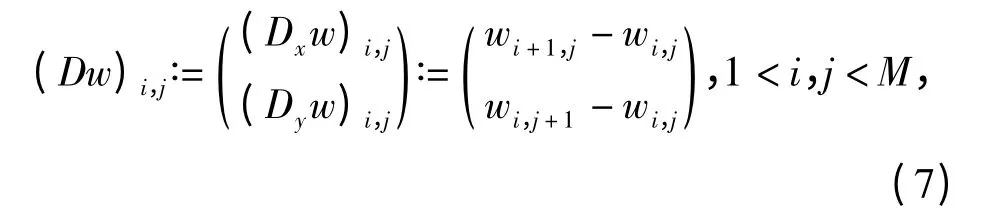
这里i=M，j=M 时采取循环边界条件，wi，j表示向量w 的第(iM+j)个分量。则

因此原始基于TV 的图像复原模型的离散化形式为

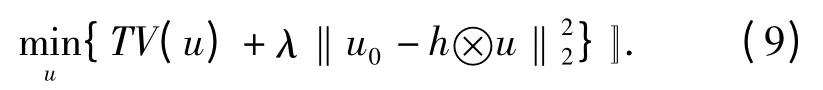
令w=h⊗u，则降质模型

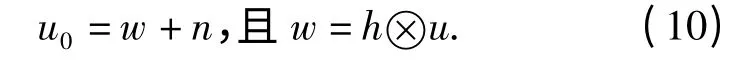
因此光学系统图像的图像复原问题等效于先去噪然后去模糊的2 个子问题迭代求解。根据TV 模型，本文构建带约束优化模型

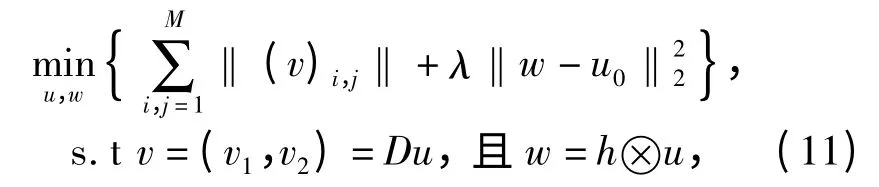
式中:‖·‖22为2－范数。利用Lagrange 乘子法将有约束问题转化为无约束代价函数最优:

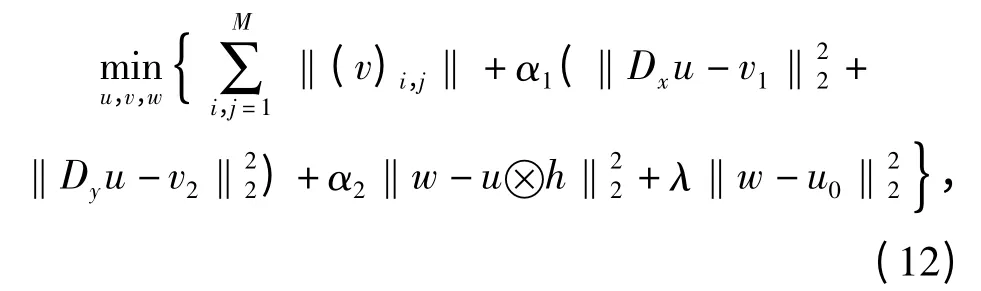
式中α1、α2为正的正则化参数。比较(12)式和(9)式，2 式之间的差别是(12)式新增了变量w 和相关的惩罚项‖w－u⊗h‖22;增加了另一个变量v 以及相关的惩罚项(‖Dxu－v1‖22+‖Dyu－v2‖22)。当α1、α2充分大时，(12)式与(9)式等价。

注意到(12)式中的代价函数包含4 项，第1 项为l1范数，而第2、第3 和第4 项为l2范数，它们都是凸的，因此代价函数是一个凸优化问题。因此根据凸分析理论，(12)式存在唯一的最优解。下面对新的代理代价函数最优设计具体的迭代过程和快速算法。

2.2 子问题优化求解

使用交替最小化算法求解(12)式。由一初值u(0)，利用该方法得到一迭代序列

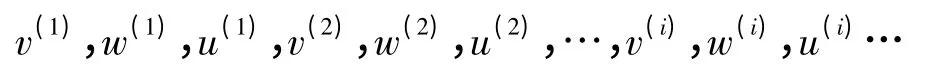
使得

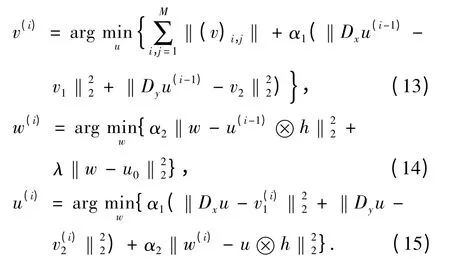
进一步考虑到:1)点扩散函数(PSF)与图像的卷积等价于调制传递函数与图像傅里叶变换的乘积;2)采取循环边界条件的向前差分算子与图像作用的过程可以表示为线性卷积过程，同样可以转化为向前差分算子形成的循环矩阵的傅里叶变换与图像傅里叶变换的乘积;3)傅里叶变换属于线性变换，不会改变欧式范数(Parseval 定理)的性质。则记F(u)，F(u0)，F(w)，F(Dx)，F(Dy)，F(h)分别为u，u0，w，Dx，Dx，h 的傅里叶变换，并分别令α =因此最小化问题(13)～(15)式可重写为

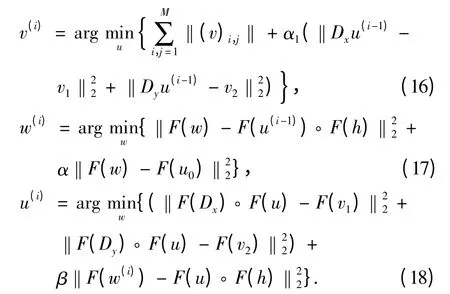
下面分别对3 个子问题的最优解进行推导，并给出计算公式。

v－子问题(13)式:u(i－1)固定时，直接进行演算，该问题对应的解为

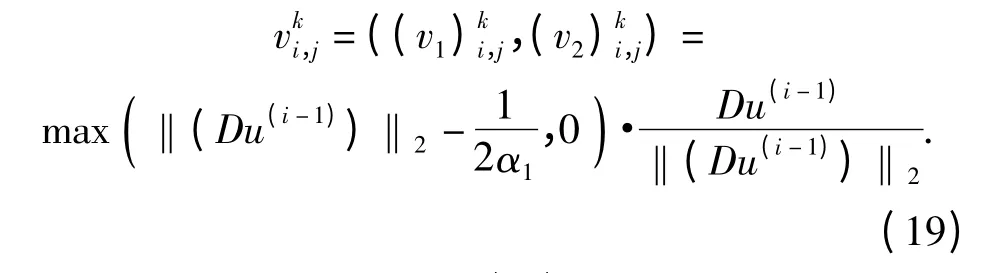
w－子问题(17)式:当u(i－1)固定时，其目标代价函数是关于F(w)的二次泛函，其解可以显式的表示为

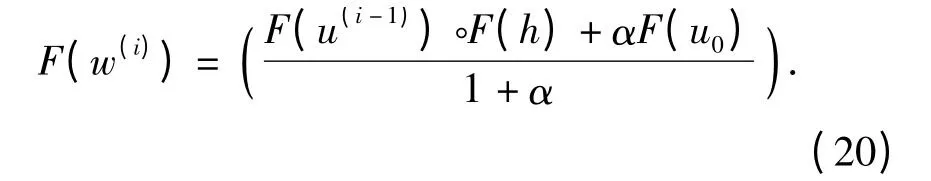
由(20)式可以看出，F(w(i))可以看作是第i－1 次的校正频谱F(u(i－1))与原始图像频谱的插值，相当于进行了一次频谱校正。

u－子问题(18)式:将F(v(i))和F(w(i))固定，求(18)式的最小解可以显示表示为

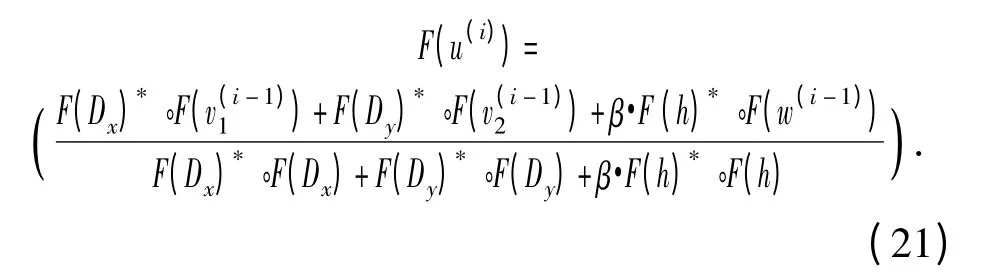
其中(20)式和(21)式“◦”表示矩阵点积，“* ”表示复共扼。

进一步进行逆傅里叶变换可得

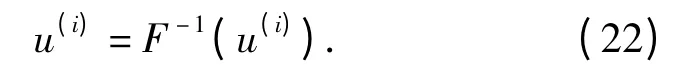
(22)式表明，u－子问题等效于图像高频信息与w－子问题求解得到的插值校正频谱信息F(w(i))的频谱重新校正过程。整个过程表明三阶段解析迭代过程具有较好的频谱外推特性。

2.3 参数选择

从上节可以看出，构建原始全变差图像恢复模型的代理代价函数的好处是等效地将模型(9)式转化为3 个简单子问题的迭代求解过程，而3 个子问题最优均具有显式解析解。三阶段解析迭代仅需要输入降质图像u0，正则化参数α1，α2， (λ 或者等效参数以及迭代终止误差参数。

由于本文算法中目标代价函数当α1，α2充分大时，才能很好地逼近于全变差复原模型。因此基于延拓方法的思想［14］，本文设置α1，α2的最大上限值α1max和α2max，在迭代过程中逐渐调整α1，α2的值达到最大上限。终止条件采取α1，α2的最大上限值α1≥α1max或α2≥α2max以及Re Diff= ‖u(i+1)－u(i)‖2/‖u(i+1)‖2＜ξstop进行控制。

基于全变差模型的图像复原算法能够较好地克服“寄生波纹效应”，但是全变差模型容易产生“阶梯效应”，特别是参数λ 的选择对“阶梯效应”的产生有影响;不恰当的λ 容易导致平坦区域的“阶梯效应”非常明显，从而降低复原图像的信噪比。根据代理函数模型，λ 的作用是平衡正则化项和保真项‖w－u0‖22惩罚之间的权衡参数。按照人眼对图像的感知特性，人眼对图像刺激的响应较少依赖于绝对亮度，而更依赖于对周围亮度的局部对比度变化。Weber－Fechner 定律［15］表明在一个相当宽的变化范围内，主观上刚可辨别亮度差异Δu 与背景的亮度u 之比称为Weber 比，它是一个常数(约为2%).另一方面图像平坦区域由于其本身方差很小且人眼对该区域的“阶梯效应”最为敏感，可认为方差的增加纯粹是噪声和“阶梯效应”引起的，因此应增加正则化项的作用，即选取较小的λ;而边缘区，由于其方差本身较大以及人眼的掩盖效应，使得人眼对该区域的“阶梯效应”不敏感，因此应增加保真项的惩罚，选取较大的λ，纹理区域应介于边缘区和平坦区之间。λ 的选择可通过图像的局部方差和梯度信息进行。由于在算法迭代过程中由(19)式我们可得到图像的梯度信息vki，j，因此本文构造自适应

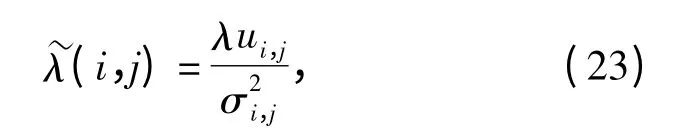
式中σi，j采取鲁棒性方差自动估计方法［16］，σi，j=1.486·median‖vki，j－median|vki，j|‖.

2.4 快速算法描述与复杂度分析

综合3.2 和3.3 节，本文算法可归结为如下步骤:

初始化:u0=u0，正则化参数α1，α2，λ，最大上限值α1max和α2max，迭代终止误差ξstop.

解析迭代

while α1＜α1max或α2＜α2maxdo

1)固定u(i－1)，根据(19)式计算梯度信息vii，j;校正得到F(w(i));

3)空域vki，j的梯度信息进行FFT 得到F(v1(i))，

2)根据(20)式在傅里叶变换域进行线性频谱F(v2(i))，连同步骤2)得到的F(w(i))代入(21)式计算F(u(i))，并进行快速IFFT 得到u(i);

4)根据(23)式进行参数更新。

终止条件判断:

如果Re Diff =‖u(i+1)－u(i)‖2/‖u(i+1)‖2＞ξstop，α1= 2α1，α2= 2α1，按照(23)式自适应调整(i，j)，重新迭代。否则输出u(i)，算法结束。

本文算法属于变量分离的子问题分裂算法，包含3 个子问题的求解。v－子问题对应的解析求解vki，j的算法复杂度为O(M2);而w－子问题和u－子问题的过程中，F(Dx)，F(Dy)，F(h)*，F(h)在迭代过程中保持不变，可以预先计算;解析求解F(w(i))和F(u(i))需要2 次快速傅里叶变换和一次快速逆傅里叶变换，其复杂度为O(M2lgM2)=O(M2lgM).而算法本质上是利用傅里叶变换对循环矩阵的对角化特性，与共扼梯度法一样属于有限步收敛算法。因此算法的整体复杂度为O(M2lgM).

关于本文算法的空间复杂度，由于预先存储的F(Dx)，F(Dy)，F(h)*，F(h)等信息均与图像的大小相同，因此空间复杂度为O(M2).

3 实验结果与分析

文中所有算法均在MATLAB 7.1 平台实现，计算环境为IBM W510 笔记本电脑、Intel 1.73 GHz CPU，3 G 内存。为了验证本文算法的有效性。用于定量评估去模糊算法的性能指标采取改进信噪比(ΔSNR)、峰值信噪比(PSNR)和相对误差(ReErr).设u0，u ，u* 分别为M ×N 的降质图像、参考图像和去模糊图像，ΔSNR、PSNR 和ReErr 定义如下:

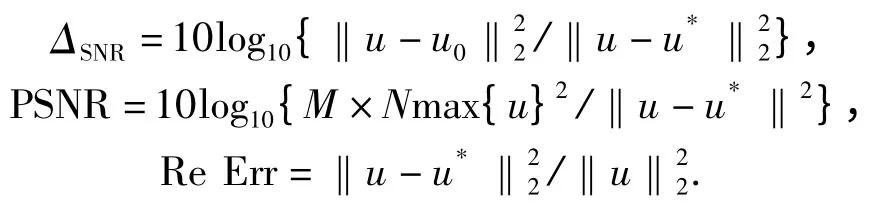
一般而言改进信噪比、峰值信噪比越大越好，而相对误差越小越好。为了更好地评价算法的结构保持特性，本文采取结构相似度指标(SSIM)来评价图像的恢复质量［17］。SSIM 指标与人类视觉特性基本吻合，与人的主观测评图像质量有较好的匹配性。实验中对比算法包括:MATLAB 7.1 中Wiener滤波、约束最小二乘算法(RLS)，Lucy－Richardson 算法;同时我们和全变差交替子空间投影算法(TVAP)［13］和文献［14］中FTVd 算法进行的对比。本文算法中初始化参数α1=α2=320，α1max=α2max=40 000，参数λ 初值为1.0，迭代过程由(23)式估计。TVAP、FTVd 和本文算法迭代终止条件均取为Re Diff=‖u(i+1)－u(i)‖2/‖u(i+1)‖2＜10－4.实验中图1(a)为一幅清晰的512 ×512 光学遥感图像，遥感成像系统MTF 模拟曲线如图1(b)所示。图2(a)为根据降质模型模拟生成的降质图像，其中加入噪声为均值为0、方差为15 高斯噪声。从图2(b)－(f)所示复原图像的视觉质量来看，约束最小二乘(RLS)算法和Lucy－Richardson 算法对于“寄生波纹效应”有所改善，但“阶跃”边缘和线状边缘保持效果不好。FTVd 算法和TVAP 的结果图像能够极大地减少“寄生波纹效应”，但视觉上的“阶梯效应”较为明显。本文算法的复原图像(如图2(f))很好地克服了两方面的不利影响，并且复原图像的细节较为清晰。

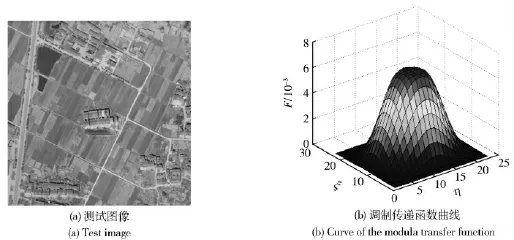
图1 实验图像与成像系统MTFFig.1 The test image and MTF of the imaging system

从复原算法的图像质量客观评价指标来看，本文算法虽然与TVAP 同样利用了全变差模型，由于TVAP 基于Chambolle 投影［11］的精确求解算法，图像质量的客观评价指标有所改善。而本文算法中通过自适应调整参数(i，j)，图像质量的客观评价指标得到进一步改善。表1给出了关于样本图像图2(a)的各类指标的提升情况，可以看到本文算法的PSNR 比FTVd 提高0.6 dB，而本文算法的ΔSNR比FTVd 提高0.3 dB.另外，本文算法取得了较好的SSIM 指标，表明图像的结构保持性能很好。

从算法所花费的CPU 时间来看，Lucy－Richardson 算法和RLS 算法是经典迭代的算法，时间较长，分别需要34.76 s 和7.11 s.TVAP 算法和FTVd、本文算法虽然都属于迭代算法，但因为前者采取了Chambolle 投影算法，而FTVd 采用了变量分离算法，都是目前快速全变差算法，时间较短。而本文算法仅用了1.36 s 就达到优于FTVd 算法的图像质量，因此本文算法得到了很好的图像质量－计算时间性价比。

图2 不同算法的复原图像Fig.2 Recovered images of different algorithms

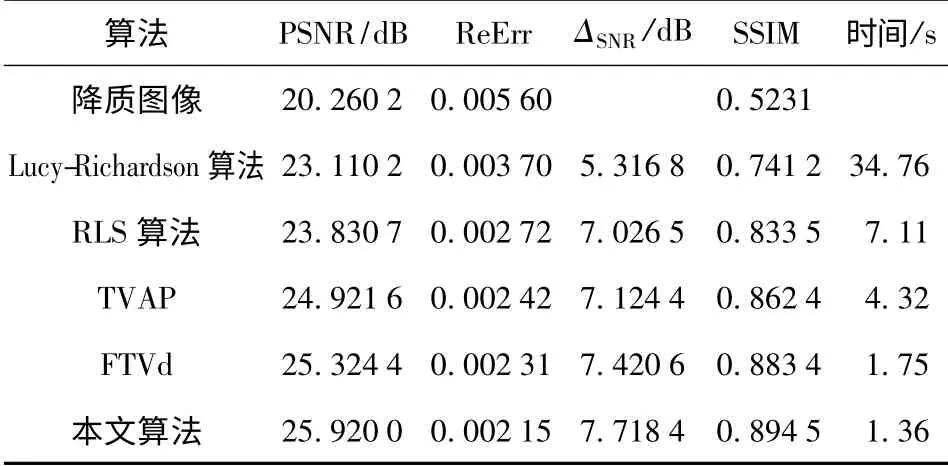
表1 不同复原算法性能指标比较结果Tab.1 Quantitative comparison between the proposed algorithm and state－of－the art algorithms

4 结论

本文给出了基于全变差图像复原模型的一种三阶段解析迭代快速复原算法，该算法基于辅助变量的全变差代理代价函数模型，将图像复原转化为3个子优化问题;并通过分析代理代价函数特殊的结构，得到了算法时间复杂度仅为O(M2logM)的三阶段解析迭代快速复原算法。算法考虑了人眼对图像平坦区域和边缘区域噪声的感知特性，通过估计迭代系统中自适应的正则化参数，较好克服了“阶梯效应”，改善了图像复原的效果。实验证明算法是一种适应于非纹理图像的优良复原算法。需要指出，对于实际光学遥感图像的复原，一般需要对模糊系统进行辨识，本文算法是假设系统点扩散函数已知的图像非盲复原，对于融合模糊辨识的盲复原算法将是下一步的主要工作;另外联合稀疏性和正则性［18］的图像复原也是重要的研究方向。

References)

［1］ Mohammal D A.Super－resolution:a short review，a new method based on hidden Markov modeling of HR image and future challenges［J］.Computer Journal，2009，52(1):126－141.

［2］ 邹谋炎.反卷积和信号复原［M］.北京:国防工业出版社，2001.ZOU Mou－yan.De－convolution and signal restoration［M］.Beijing:National Defense Industry Press，2001.(in Chinese)

［3］ 张晶晶，方勇华.基于Contourlet 变换的遥感图像去噪新算法［J］.光学学报，2008，28(3):462－466.ZHANG Jing－jing，FANG Yong－hua.Novel denoising method for remote sensing image based on contourlet transform［J］.Acta Optica Sinica，2008，28(3):462－466.(in Chinese)

［4］ 刘扬阳，金伟其，苏秉华，等.基于超分辨力图像复原算法的模糊系统辨识［J］.光电子·激光，2005 ，16(2):213－216.LIU Yang－yang ，JIN Wei－qi ，SU Bing－hua，et al.Identification of blurred system based on super－resolution reconstructing image schemes［J］.Journal of Optoelectronics Laser，2005，16(3):213－216.(in Chinese)

［5］ 孟静，王加俊，黄贤武，等.一种光学层析图像的多准则重建方法［J］.光学学报，2006，26(9):1340－1344.MENG Jing，WANG Jia－jun，HUANG Xian－wu，et al.Multi－criterion reconstruction method for optical tomography［J］.Acta Optica Sinica，2006，26(9):1340－1344.(in Chinese)

［6］ Shao W Z，Wei Z H.Edge－and－corner preserving regularization for image interpolation and reconstruction［J］.Image and Vision Computing，2008，26:1591－1606.

［7］ 王怀野，张科，李言俊.各向异性滤波在红外图像处理中的应用［J］.红外与毫米波学报，2005，24(2):109－112.WANG Huai－ye，ZHANG Ke，LI Yan－jun.Anisotropic Gaussian filtering for infrared image［J］.Journal of Infrared And Millimeter Waves，2005，24(2):109－112.(in Chinese)

［8］ 洪汉玉，张天序，余国亮.航天湍流降质图像的极大似然估计规整化复原算法［J］.红外与毫米波学报，2005，24(2):130－134.HONG Han－yu，ZHANG Tian－xu，YU Guo－liang.Regularized restoration algorithm of astronautically turbulence degraded images using maximum－likehood estimation ［J］.Journal of Infrared and Millimeter Waves，2005，24(2):130－134.(in Chinese)

［9］ Rudin L，Osher S，Fatemi E.Nonlinear total variation based noise removal algorithms［J］.Physica D，1992，60(1－4):259－268.

［10］ Marquina A，Osher S J.Image super－resolution by TV－regularization and Bregman iteration［J］.Journal of Scientific Computing，2008，37:367－382.

［11］ Chambolle A.An algorithm for total variation minimization and application［J］.Journal of Mathematical Imaging Vision，2004，20(1):89－97.

［12］ Chen K，Tai X C.A nonlinear multigrid method for total variation minimization from image restoration ［J］.Journal of Scientific Computing，2007，33(2):115－138.

［13］ Huang Y M，Micheal K NG，Wen Y W.A fast total variation minimization method for image restoration［J］.Muti－scale Model Simulation，2008，7(2):774－795.

［14］ Wang Y，Yang J，Yin W，et al.A new alternating minimization algorithm for total variation image reconstruction［J］.SIAM Journal on Imaging Sciences，2008，1(3):248－272.

［15］ Shen J H.On the foundations of vision modeling，I.Weber’s law and Weberized TV restoration［J］.Physica D:Nonlinear Phenomena，2003，175(3－4):241－251.

［16］ Black M，Sapiro G.Edge as outiers:anisotropic smoothing using local image statistics［C］∥Proceedings of the Scale－space Conference.Berlin:Springer－Verlag，1999:259－270.

［17］ Wang Z，Bovik A C，Sheikh H R，et al.Image quality assessment:from error visibility to structural similarity［J］.IEEE Transaction on Image Processing，2004，13(4):600－612.

［18］ Afonso M V，Bioucas－Dias J M，Figueiredo M A T.Fast image recovery using variable splitting and constrained optimization［J］.IEEE Transaction on Image Processing，2010，19(9):2345－2356.