基于Copula的机械系统可靠性模型及其应用

何成铭，吴纬，孟庆均

(1.装甲兵工程学院，北京100072;2.北京特种车辆研究所，北京100072)

0 引言

机械系统各组成单元及其失效模式之间具有复杂的相关性，这是机械系统区别于电子系统的显著标志之一，如何精确刻画这种相关性是机械系统可靠性设计与分析中亟待解决的关键问题之一［1－2］。近年来，一些学者在金融、保险和工程等领域，应用连接函数Copula 探讨相关性，取得了较为满意的效果［3－5］。文献［6－9］探讨了应用Copula 函数及有关理论解决机械系统可靠性中的相关性问题，尽管探讨只是初步的，还没有达到实用的程度，但却表明Copula 理论在解决机械系统可靠性相关性问题方面前景十分广阔。本文在前人工作的基础上，系统构建了基于Copula 的机械系统可靠性模型，并将其应用于某型装甲装备悬挂系统的可靠性预计中。

1 理论依据

Sklar 在1959年指出，可将一个联合分布分解为k 个边缘分布和一个Copula 函数，这个Copula 函数可描述变量之间的相关性［10］。Copula 函数实际上是一类将联合分布函数与它们各自的边缘分布函数连接在一起的函数，因此，也将它称为连接函数。

1.1 Copula 函数的定义与性质

用Rn记拓展的n 维空间(n 是任意的正整数)，a=(a1，a2，…，an)表示Rn中的点。对所有的k，如果都有ak≤bk，就说a≤b.对a≤b，用［a，b］=［a1，b1］×［a2，b2］×…×［an，bn］表示n 维立方体，其体积记为VC(［a，b］).

定义1［11］Copula 函数是指具有以下性质的函数C(·，…，·):

1)C(·，…，·)的定义域为In，即［0，1］n;

2)对In中的任意u，若u 中至少一个分量为0，则C(u)=0，若除uk外，u 中的所有分量都为1，则C(u)=uk;

3)对In中的a，b(a≤b)，VC(［a，b］)≥0，即C(·，…，·)有基底且是n 增函数。

定义2［11］若∀(u1，u2，…，un)∈In，C1(u1，u2，…，un)≤C2(u1，u2，…，un)，则称Copula 函数C1(·，…，·)＜C2(·，…，·)(或C2(·，…，·)＞C1(·，…，·))，记作:C1＜C2(或C2＞C1).

n 维Copula 的Freche－hoeffding 上、下界分别为

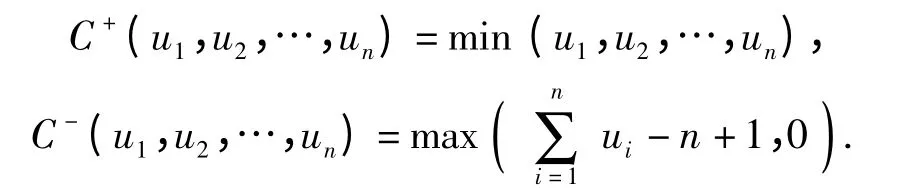
根据上述定义，可推导出Copula 函数(简记为C)的一些基本性质［3］:

1)对任意变量ui∈［0，1］，i =1，2，…，n，C(u1，u2，…，un)都是非减的;

2)C(u1，u2，…，0，…，un)=0，C(1，…，1，ui，1，…，1)=ui;

3)∀ui，vi∈［0，1］，i = 1，2，…，n，均有|C(u1，u2，…，un)－C2(v1，v2，…，vn)|

4)C－＜C ＜C+;

5)若变量ui∈［0，1］，i =1，2，…，n 相互独立，则记为C⊥.

1.2 Sklar 定理

定理［10］设H 是n 维分布函数，它的边缘分布为F1(·)，F2(·)，…，Fn(·)，那么对Rn中的所有X，存在一个n 维Copula C，使得

如果F1(·)，F2(·)，…，Fn(·)连续，则C 是唯一的。否则C 的唯一性在RanF1× RanF2× … ×RanFn上确定。反之，如果C 是n 维Copula，F1(·)，F2(·)，…，Fn(·)是分布函数，那么存在由(1)式定义的n 维分布函数H，它的边缘分布为F1(·)，F2(·)，…，Fn(·).

推论［6］设X1，X2，…，Xn是随机变量，它们的分布函数分别是FX1(x1)，FX2(x2)，…，FXn(xn)，联合分布函数为H(x1，x2，…，xn)，则存在一个n 维Copula C，使得(1)式成立。如果F1(x1)，F2(x2)，…，Fn(xn)连续，C 是唯一的。否则C 的唯一性在RanF1×RanF2×…×RanFn上确定。

通过Copula 函数C 的密度函数c 和边缘分布函数F1(x1)，F2(x2)，…，Fn(xn)，可以方便地求出n 维分布函数H(x1，x2，…，xn)的密度函数

式中:ui= Fi(xi);c (u1，u2，…，un) =是边缘分布Fi(xi)的密度函数，i=1，2，…，n.

根据Sklar 定理，利用Copula 函数，可将边缘分布和变量之间的相关结构分开研究，且降低多变量概率模型建模和分析的难度。

2 基于Copula 的机械系统可靠性模型

2.1 基于Copula 的串联机械系统可靠性模型

当机械系统由n 个单元串联而成时，设第i 个单元的寿命为Ti，Fi(t)为Ti的分布函数，可靠度为Ri(t)=P(Ti＞t)=1－Fi(t)，i =1，2，…，n，串联系统的寿命为T =min (T1，T2，…，Tn)，T1，T2，…，Tn的联合分布函数为H(t1，t2，…，tn)=P{T1≤t1，T2≤t2，…，Tn≤tn}.

由Sklar 定理，存在一个n 维Copula C，使得H(t1，t2，…，tn)=Cn(F1(t1)，F2(t2)，…，Fn(tn))，式中Cn(·)表示n 维Copula C，因为Fi(t)连续，所以Cn(F1(t1)，F2(t2)，…，Fn(tn))是唯一的。串联系统的可靠度为

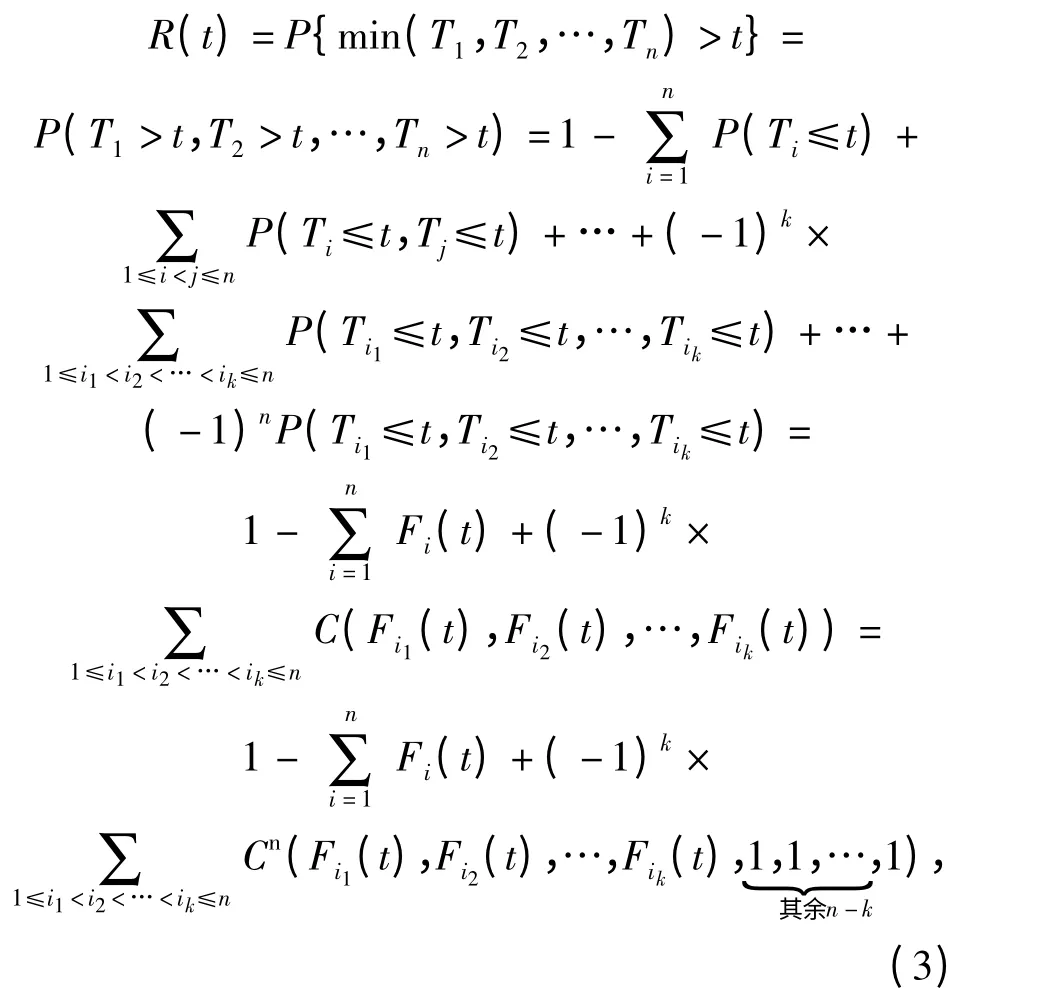
式中2≤k≤n.

2.2 基于Copula 的并联机械系统可靠性模型

对于n 个单元组成的并联机械系统，设第i 个单元的寿命为Ti，Fi(t)为Ti的分布函数，可靠度为Ri(t)=P(Ti＞t)=1－Fi(t)，i =1，2，…，n，并联系统的寿命为T =max (T1，T2，…，Tn)，T1，T2，…，Tn的联合分布函数为H(t1，t2，…，tn)=P{T1≤t1，T2≤t2，…，Tn≤tn}.

由Sklar 定理知，存在一个n 维Copula C，使得H(t1，t2，…，tn)=Cn(F1(t1)，F2(t2)，…，Fn(tn)).

并联系统的可靠度为

当各单元之间相互独立时，由

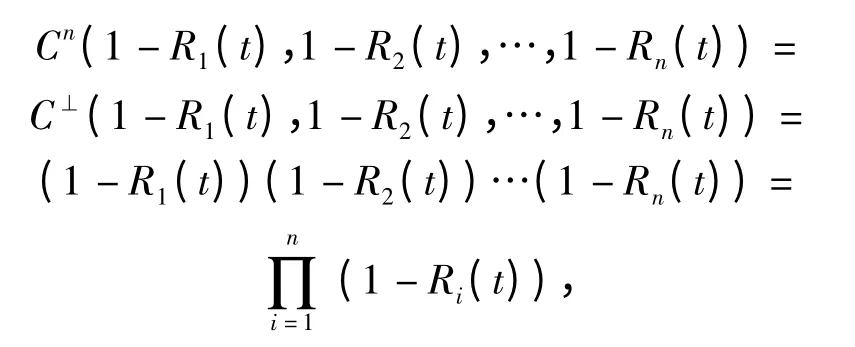
至此，本文就建立了基于Copula 的机械系统可靠性模型，这样就可在不研究多维随机变量联合分布函数的前提下，通过构造适当的Copula 函数，来求解考虑相关性时机械系统的可靠性量值，从而有效解决机械系统可靠性建模难的问题。

3 基于Copula 的机械系统可靠性模型在可靠性预计中的应用举例

利用基于Copula 的机械系统可靠性模型，通过构造能反映机械系统各组成单元相关结构特征的Copula 函数，以单元寿命为基本输入(假定各单元寿命分布规律已知)，可估计出Copula 模型的参数，从而预计机械系统的可靠性。下面以某型装甲车辆悬挂系统为例说明基于Copula 的机械系统可靠性模型在可靠性预计中的应用。

3.1 问题描述

由n 个单元组成的串联机械系统，第i 单元的寿命为Ti，其分布函数(故障概率)记为Fi(ti)，可靠度Ri(ti)=1－Fi(ti).已知各单元寿命的一组观测值(t1j，t2j，…，tnj)，j=1，2，…，w.试估计系统可靠度。

由(3)式，有

(5)式中，Fi(t)可通过确定分布类型并估计其分布参数得到;先选择合适的Copula 模型，由Copula 函数的性质，估计出Cn(F1(t)，F2(t)，…，Fn(t))的参数，令Fj(t)=1，j =ik+1，ik+2，…，n，就可以得到C(Fi1(t)，Fi2(t)，…，Fik(t))，1≤i1＜i2＜…＜ik≤n，2≤k≤n.

因而利用基于Copula 的机械系统模型预计系统可靠度的基本步骤为:

1)确定边缘分布，即单元寿命的分布类型Fi(t)，并估计其分布参数;

2)选择一个适当的Copula 函数，使之能够很好地描述各单元寿命之间的相关特征;

3)估计Copula 模型的参数;

4)计算系统可靠度。

下面对上述各步骤分别进行阐述。

3.2 单元寿命分布类型的确定及其参数估计

机械产品的寿命比较适宜于用威布尔分布来描述，威布尔分布具有较强的适应性，用三参数威布尔分布拟合机械产品寿命分布，更加符合实际，具有显著的优势。因此，本文采用三参数威布尔分布来描述单元寿命。第i 单元的寿命分布函数(故障概率)和可靠度分别为

式中γi、mi、ηi分别为第i 单元寿命威布尔分布的位置参数、形状参数和尺度参数。文献［12－13］对三参数威布尔分布提出了较为实用的参数估计方法。利用该方法可方便地求出3 个参数的估计值

3.3 Copula 模型的构建

文献［14］介绍了常用的Copula 函数，可根据需要选择。鉴于机械零部件寿命之间的相关性通常表现为正相关，同时考虑到模型参数估计和计算简便的要求，本文选用阿基米德Copula 函数族中的多元Gumbel Copula 函数。文献［8］指出Gumbel Copula函数能够比较准确地刻画机械系统的相关性。多元Gumbel Copula 函数的分布函数和密度函数分别为

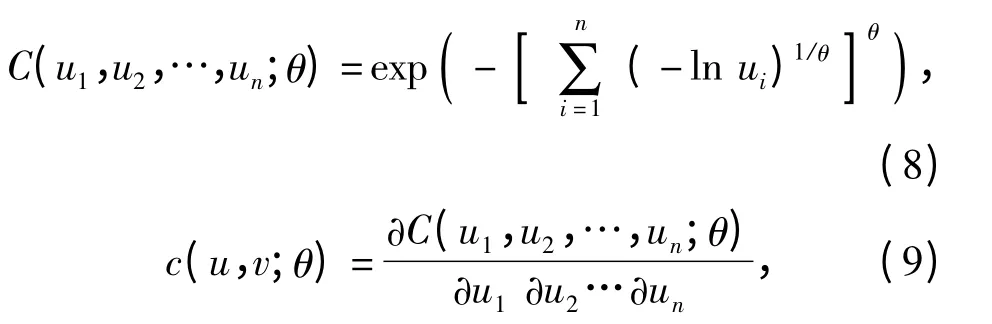
式中θ∈(0，1］为相关系数，θ=1 表示随机变量u1，u2，…，un独立，θ→0 表示随机变量u1，u2，…，un趋向于完全相关。

令ui=Fi(ti)=1－e－(ti－γi)mi/ηmi，由(8)式有

再根据(5)式，系统可靠度为

需要先估计出(10)式所示Copula 函数中参数θ 的值而后令Fj(t)=1，j =ik+1，ik+2，…，n，将和各单元威布尔分布参数估计值代入(11)式，即可求解系统可靠度。

3.4 Copula 模型的参数估计

本文采用NLP－MLE 方法［12－13］对(10)式所建立的模型进行参数估计。这里以某型装甲车辆悬挂系统为例，阐述上述Copula 模型参数估计方法。

已知某型装甲车辆悬挂系统由平衡肘、扭力轴和液压减振器组成(每台装备上各有10 件)。对5 台装备进行了寿命试验，记录了各单元的寿命数据，如表1～3 所示。

设扭力轴、平衡肘和液压减振器的寿命分别为T1、T2、T3，均服从三参数威布尔分布，分布函数分别为F1(t1)、F2(t2)、F3(t3)，由(8)式有

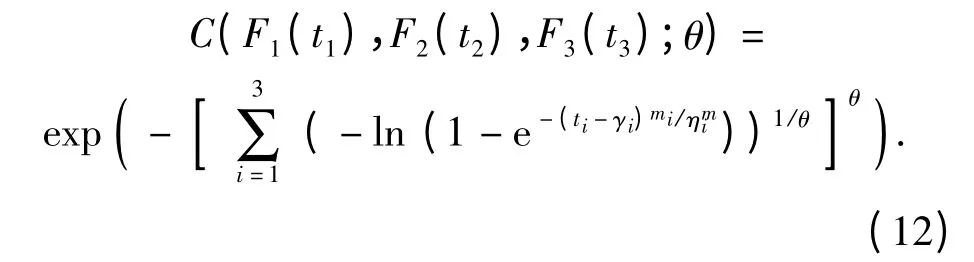
由(9)式，可得到三元Gumbel Copula 函数的密度函数为

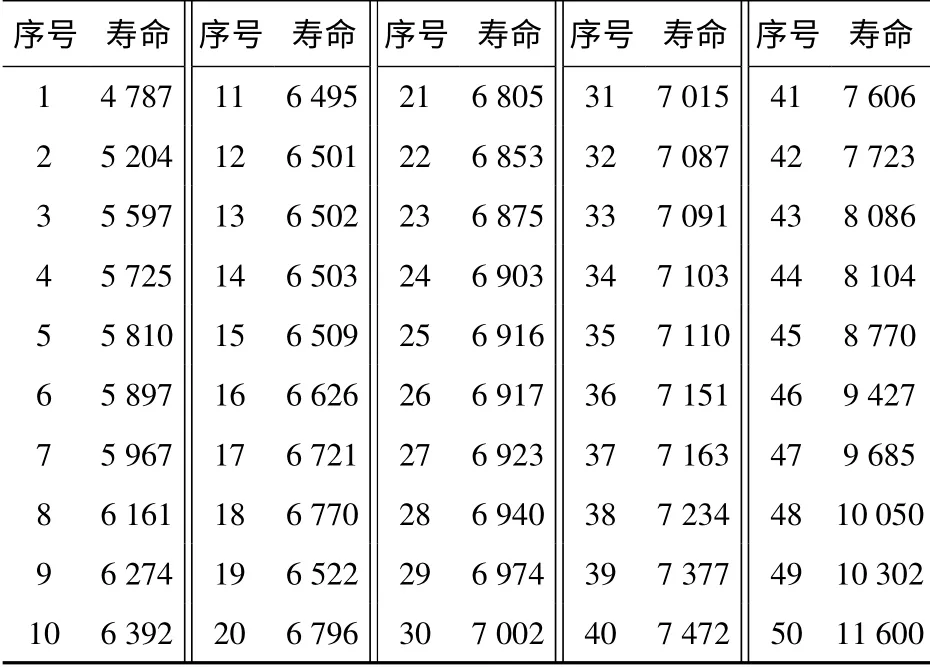
表1 某型装甲车辆平衡肘的寿命数据Tab.1 Elbow balancer’s life data for some type of armored vehicle km

表2 某型装甲车辆扭力轴的寿命数据Tab.2 Torsion bar’s life data for some type of armored vehicle km

表3 某型装甲车辆液压减振器的寿命数据Tab.3 Hydraulic shock absorber’s life data for some type of armored vehicle km

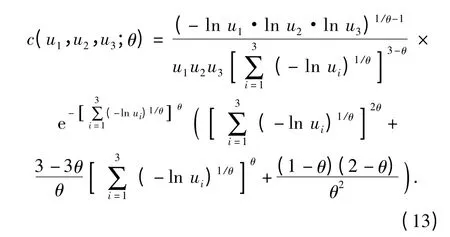
由(13)式可得到似然函数为

按照NLP－MLE 方法进行Copula 模型参数估计，需要先估计边缘分布的分布参数，用NLP－MLE方法，可得到扭力轴、平衡肘和液压减振器寿命威布尔分布的3 个参数，如表4所示。

表4 某型装甲车辆悬挂系统部件寿命威布尔分布参数估计值Tab.4 Weibull distribution parameters estimating result of suspension system for some type of armored vehicle

将表4中的数值代入(14)式。估计参数θ 的实质是寻找使(14)式取得最大值的，即将问题转化为如下的非线性规划问题:Excel的规划求解功能，可求得=0.234.

以表1～3 中的数据为基础，利用Microsoft

3.5 预计系统可靠度

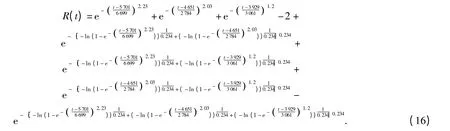
若要预计该悬挂系统在车辆行驶6 000 km 时的可靠度，将t=6 000 代入(16)式，得R(6 000)=0.532.

若不考虑单元之间的相关性，悬挂系统在车辆行驶6 000 km 时的可靠度

液压减振器是悬挂系统中可靠性最低的单元，其在车辆行驶6 000 km 时的可靠度

记基于Copula 的系统可靠度为RC(t)，假设各单元相互独立时的系统可靠度为RI(t)，薄弱环节理论对应的系统可靠度为RW(t)，由上面实例的计算结果，RC(t)= 0.532，RI(t)= 0.425，RW(t)=0.535，则显然有

这与可靠性界限模型的结论是一致的，从而也验证了基于Copula 的机械系统可靠性模型的合理性。

部队多年实际使用数据表明，该型装备悬挂系统行驶6 000 km 的损坏率为48%，相当于使用到6 000 km时悬挂系统的可靠度为0.520，略低于预计值0.532，剔除由于人为操作失误和维修不当等因素引起的损坏，可以认为该模型与实际情况是基本吻合的。这就从理论和实践2 个方面证实了模型的正确性与合理性。

4 结论

应用Copula 理论进行机械系统可靠性建模及其预计，将机械产品寿命随机变量的分布(边缘分布)和变量的相关结构分开来研究，减小了多变量概率模型建模和分析的难度，并使建模和分析过程更加清晰。机械系统可靠性中的相关性问题是普遍存在、不能回避的，基于Copula 的机械系统可靠性模型的提出，为解决机械系统可靠性建模与预计难题提供了科学实用的方法。

References)

［1］ 谢里阳，王正，周金宇，等.机械可靠性基本理论与方法［M］.北京:科学出版社，2009:118－129.XIE Li－yang，WANG Zheng，ZHOU Jin－yu，et al.The basic theories and methods of the mechanical reliability［M］.Beijing:Science Press，2009:118－129.(in Chinese)

［2］ 何成铭，吴纬，朱志杰.机械系统可靠性设计若干问题探讨［J］.装甲兵工程学院学报，2006，20(1):29－33.HE Cheng－ming，WU Wei，ZHU Zhi－jie.Discussion on some problems in mechanical system reliability design［J］.Journal of Academy of Armored Force Engineering，2006，20(1):29－ 33.(in Chinese)

［3］ 韦艳华，张世英.Copula 理论及其在金融分析上的应用［M］.北京:清华大学出版社，2008:1－33.WEI Yan－hua，ZHANG Shi－ying.Copula theory and its applications in financial analysis ［M］.Beijing:Tsinghua University Press，2008:1－33.(in Chinese)

［4］ 张尧庭.连接函数(Copula)技术与金融风险分析［J］.统计研究，2002，(4):48－51.ZHANG Yao－ting.Copula technique and financial risk analysis［J］.Statistical Research，2002，(4):48－51.(in Chinese)

［5］ 罗俊鹏.Copula 理论及其在金融分析中的应用研究［D］.天津:天津大学，2005.LUO Jun－peng.Copula theory and its applications in the financial analysis［D］.Tianjin:Tianjin University，2005.(in Chinese)

［6］ 易文德.应用Copula 探讨可靠性理论中的相依性［D］.成都:西南交通大学，2005.YI Wen－de.Application Copula explore dependencies in reliability theory［D］.Chengdu:Southwest Jiaotong University，2005.(in Chinese)

［7］ 易文德.简单系统相依部件的可靠性［J］.渝西学院学报:自然科学版，2005，4(2):5－8.YI Wen－de.The reliability of interdependent parts in simple systems［J］.Journal of Western Chongqing University:Nature Science，2005，4(2):5－8.(in Chinese)

［8］ 唐家银，赵永翔，何平，等.机械系统相关性可靠度计算的Copula 新理论［J］.机械科学与技术，2009，28(4):532－535.TANG Jia－yin，ZHAO Yong－xiang，HE Ping，et al.Copulas new theory for reliability calculation involving correlation in mechanical systems［J］.Mechanical Science and Technology for Aerospace Engineering，2009，28(4):532－535.(in Chinese)

［9］ 侯兵.Copula 在可靠性理论中的运用［J］.西南民族大学学报:自然科学版，2008，34(4):660－662.HOU Bing.Application of Copulas in reliability theory［J］.Journal of Southwest University for Nationalities:Natural Science Edition，2008，34(4):660－662.(in Chinese)

［10］ Sklar A.Fonctions de repartition àn dimensions et leura marges［J］.Publication de 1’Insititut de Statictique de 1’Université de Paris，1959，8:229－231.

［11］ Nelsen R B.Anintroduction to Copulas［M］.New York:Springer，2006.

［12］ 史景钊，杨星钊，陈新昌.3 参数威布尔分布参数估计方法的比较研究［J］.河南农业大学学报，2009，43(4):405－409.SHI Jing－zhao，YANG Xing－zhao，CHEN Xin－chang.Comparative study on parameter estimation methods for 3－parameter Weibull distribution［J］.Journal of Henan Agricultural University，2009，43(4):405－409.(in Chinese)

［13］ 何成铭.装甲车辆机械系统可靠性设计方法研究［D］.北京:装甲兵工程学院，2010.HE Cheng－ming.Research on mechanical system reliability design method for armored vehicle［D］.Beijing:Academy of Armored Forces Engineering，2010.(in Chinese)

［14］ Genest C，Machay J.The joy of Copulas:bivariate distributions with uniform marginal［J］.American Statistician，1986，40:280－283.