基于神经网络的双馈风电矢量控制系统转速辨识

王娟平，程书华

（山西电力职业技术学院，山西 太原 030021）

变速恒频风力发电系统，是一个复杂、不稳定、强耦合、多变量的非线性系统，其系统参数具有很强的不确定性，很难建立精确的数学模型。在很多研究中，人们将矢量控制应用于双馈风力发电系统中，实现了发电机输出频率不再影响原动机转速，发电机输出电压（或电流）的频率、幅值、相位也不受转子转速和转子瞬时位置的影响[1]，基本完成了风力发电这一非线性系统的解耦控制。

然而，传统的矢量控制技术，大多采用位置传感器来检测转子转速，给风力发电系统带来了较大的维护工作量，降低了风力发电机的可靠性和适应性。为此，近年来双馈发电机的无速度传感器矢量控制方法，成为研究风电系统的热门课题。

文献[2]提出一种基于转子电流的模型，参考自适应系统（MRAS）的双馈感应电机（DFIM）无速度传感器控制方法；

文献[3]通过采用PI自适应算法，构造了一种新型转速辨识的无速度传感器风电矢量控制方法；

本文在文献[3]的基础上，设计出一种基于神经网络的双馈风力发电机的转速估计方法，并在MATLAB/Simulink环境下，对该系统进行动态仿真研究，研究结果表明，该转速估计方法具有良好的快速逼近性。

1 无速度传感器双馈风电矢量控制系统原理

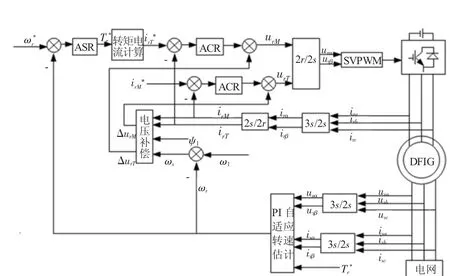
图1 基于PI自适应转速估计的无传感器矢量控制系统框图

图1 为基于PI自适应法进行转速估计的无传感器风电矢量控制系统转子侧模型。从图中可以看出，转子侧系统采用转子电流、转子转速双闭环控制。其中，内环为转子电流控制环，通过检测转子相电流，经过3s/2s和2s/2r两步变换，得到同步旋转坐标系下的irM、irT两个控制通道，通道中转子电流的给定值与irM、irT比较后的误差，经带积分和输出限幅的PI型电流调节器调节后输出电压控制量，该电压控制量分别叠加前馈电压补偿量△urM、△urT后，得到转子电压控制量，转子电压控制量再经2r/2s变换、SVPWM调制后产生发电机转子侧实际所需的励磁电压和励磁电流，实现双馈风力发电矢量控制系统转子侧的解耦控制。

图1矢量控制系统的外环为转子转速控制环，与电流内环类似，转速的给定值与转速的反馈值比较后所得的差值，经PI调节器调节后，得到发电机的输出转矩，输出转矩再经转矩电流计算，得到转子电流有功分量的给定值。而转子电流无功分量的给定值，通常是按照电网对风力发电矢量控制系统的无功要求计算得到的。该系统中，电机转速反馈值的检测，是通过PI自适应速度辨识方法来估计的，利用自适应控制原理，使系统对转子参数的鲁棒性大大提高，但同时仍然引入了PI调节器，使得系统动态估计精度受到影响[3]。

2 神经网络转速辨识

神经网络转速辨识的基本原理，如图2所示，采用离线训练、在线运行的方法，对原系统的输入、输出数据直接学习，通过调节其权值来映射原非线性系统，实现以任意精度逼近该非线性系统，从而进行参数估计和转速辨识。这种控制理论的自适应自组织能力、泛化能力和非线性映射能力很强，与传统的PI调节自适应控制相比，可弥补其不足，使其对参数的变化和系统的噪声具有很强的鲁棒性[4]。

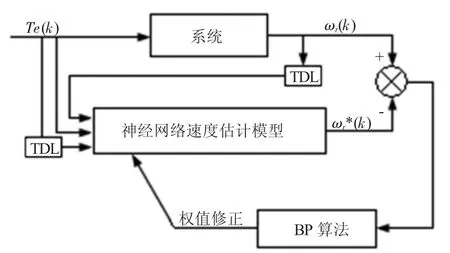
图2 神经网络转速辨识的基本原理

图2 中，“系统”是由PI自适应算法所建立的非线性模型，其非线性关系经过离散化后如下式所示：

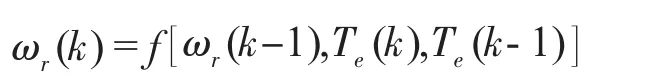
这一非线性关系，可以由神经网络来映射[4]，只需提供足够多的输入、输出样本数据，对神经网络进行严格的学习训练，使该神经网络逼近原PI自适应算法所建立的系统，进而映射原PI自适应算法所建立系统的非线性关系，实现用神经网络模型对风力发电系统的控制。

在众多的神经网络模型中，基于BP算法的神经网络（即BP网络）发展最为成熟。在使用BP网络时，关键问题在于神经网络的结构设计上，即如何选择网络的层数和每层节点数。

本文使用的神经网络转速辨识模型，是对PI自适应算法的输入、输出样本数据进行反复训练改进后所确定的，其结构如图3所示。

图中，x1、x2和 x3为系统输入，分别代表

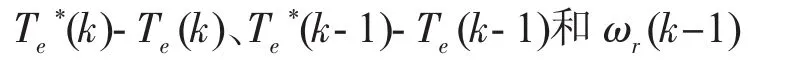
ωr为辨识对象的输出，ωr*为神经网络模型的输出，选择tan-sigmoid函数作为隐含层的激活函数，purelin函数作为输出层的激活函数，可得网络的训练样本集。

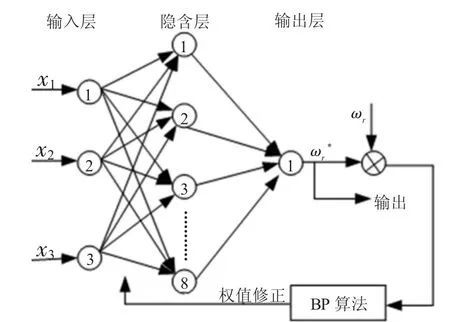
图3 神经网络转速辨识结构模型

3 BP神经网络控制系统仿真

以PI自适应速度估计为基础，对基于PI自适应速度估计的无传感器矢量控制系统中的PI调节器，用BP神经网络来代替，对转速进行辨识，得到了BP神经网络速度辨识系统。图4给出了MATLAB/Simulink环境下搭建的基于BP神经网络的转速辨识模型。

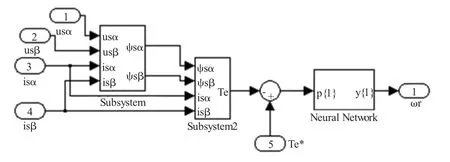
图4 基于神经网络的转速辨识模型

图5 为利用Matlab中的nntool工具箱建立的BP网络，即神经网络部分。

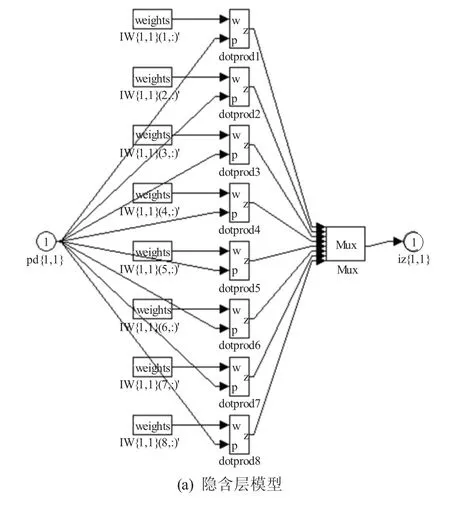
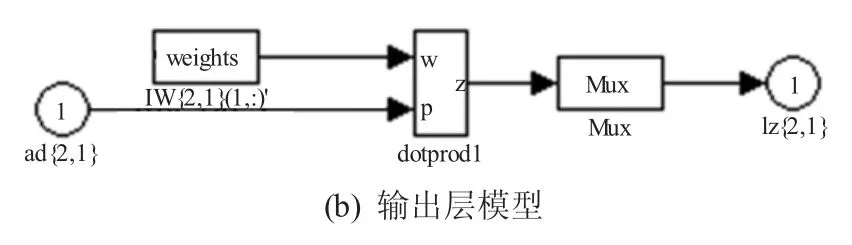
图5 BP网络模型

为验证应用BP神经网络估计发电机转速的实际效果，对该系统作了仿真。

当发电机工作在亚同步速（ω=135 rad/s）和超同步速（ω=152 rad/s）时，其系统转速的变化曲线分别如图6和图7所示。而当发电机的工作状态从亚同步速（ω=135 rad/s）状态切换到超同步速（ω=152 rad/s）状态时，其系统转速的变化曲线如图8所示。图中标有线标1的曲线为实际转速曲线，标有线标2的曲线为PI自适应辨识转速曲线，标有线标3的曲线为神经网络辨识转速曲线。

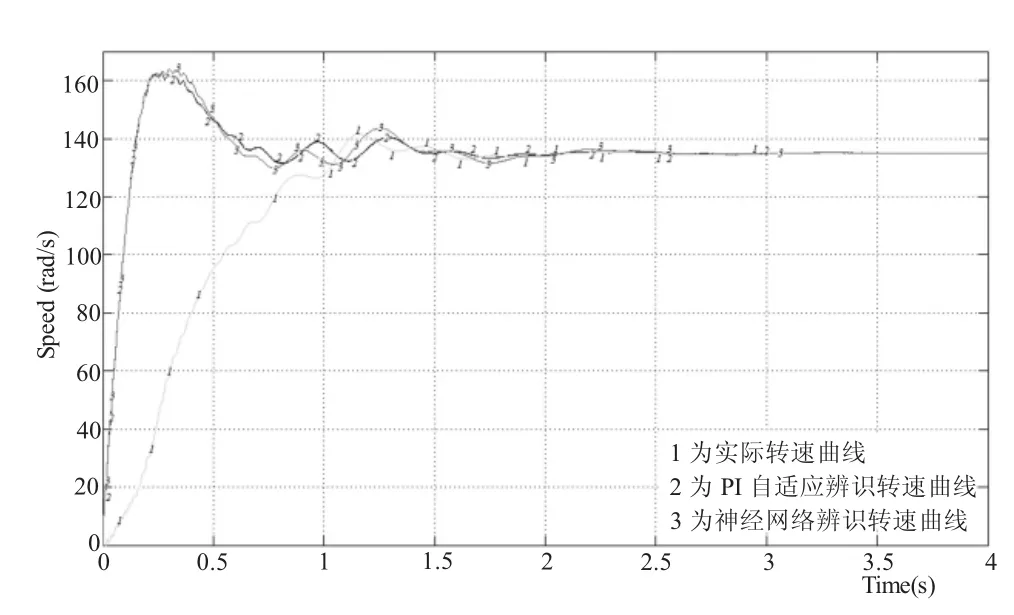
图6 给定转速ω=135 rad/s时发电机转速变化波形

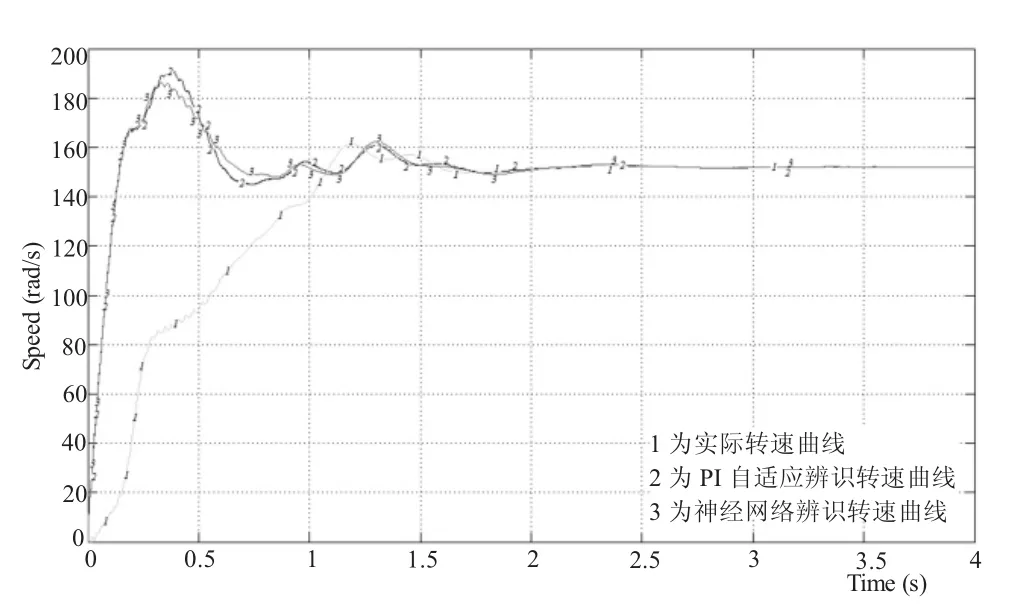
图7 给定转速ω=152 rad/s时发电机转速变化波形

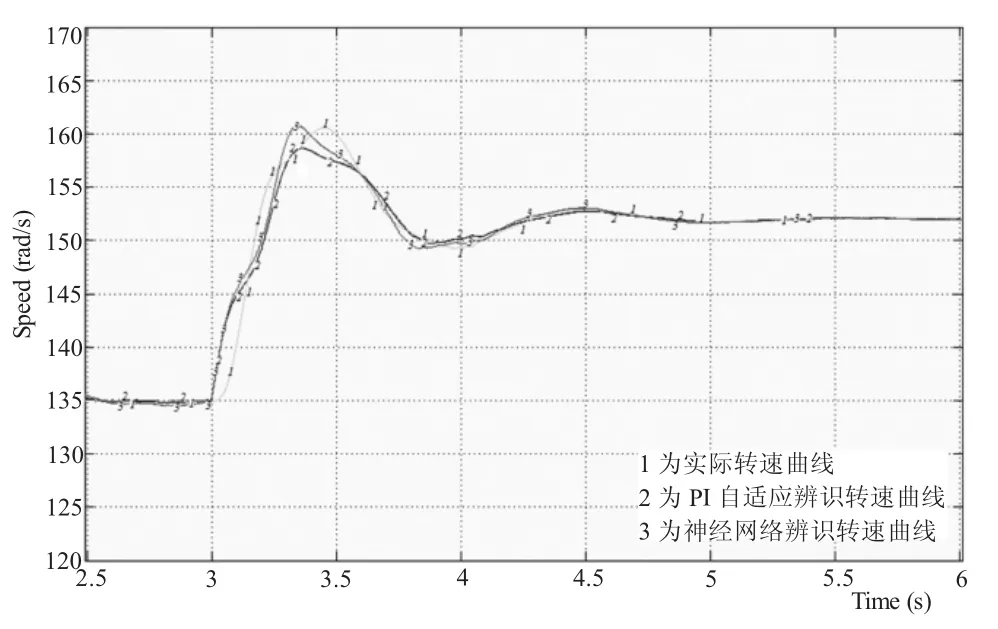
图8 发电机从亚同步状态切换到超同步状态时的转速变化波形

从图6、图7和图8的转速变化曲线可知，无论发电机工作于亚同步状态、超同步状态还是从亚同步状态过渡到超同步状态，采用PI自适应和神经网络两种方法对速度进行辨识的结果都优于实际转速，表现在两种方法的响应速度较快、抗外界干扰能力较灵敏、过渡过程中转速的超调量较小。但三种转速均能跟踪转速给定，且神经网络对速度的辨识，很接近PI自适应法对速度的辨识。

4 结束语

神经网络作为智能控制的一种，对于不能精确确定数学模型的非线性系统，具有良好的辨识能力和动态性能，采用该理论进行速度辨识，非常适用于双馈风力发电矢量控制系统中发电机转速的在线动态检测。且该方法自学习、自适应能力很强，一旦经过严格训练，便能以任意精度逼近原非线性系统，为非线性系统辨识提供了一个强有力的工具。

[1]刘宝英.并网型风力发电机组控制技术综述[J].机电信息，2009，（36）：66-68.

[2]高 乐，周有庆，徐隆亚，等.基于转子电流的双馈感应电机无速度传感器控制[J].电力系统自动化，2010，34(13)：61-65.

[3]李 岚，王 颖.双馈风力发电系统PI自适应速度估计[J].微特电机，2007，（3）：8-10.

[4]雷 华.感应电动机的神经网络速度估计方法研究[D].重庆：重庆大学，2003.