应急配送网络模型分析——以天气随机变化为考虑因素

○ 俞秋婷 张岐山

（福州大学管理学院 福建 福州 350108）

一、引言

应急物流配送网络设计是一个复杂系统，它的模型既可以是确定性的，也可以是不确定性的。在确定性模型中，获得的信息都是确定值；而不确定性模型中，获得的信息可以是不确定的，包括需求的不确定、路径选择的不确定、车辆选择的不确定，还包括随机不确定、模糊需求不确定和灰色不确定等。国内外的学者对于确定性应急物流配送网络作了较为细致全面的研究，通过建立整数规划或者混合整数规划、双层规划模型、多目标模型描述应急物流配送网络。为了使所建立的模型越来越接近现实，越来越多的应急物流配送网络的研究引入了模糊变量、随机变量、灰变量。

目前，大多数的研究都集中在对需求的模糊性或随机性、运输时间的模糊性以及灾难对于路径破坏的模糊性上，极少考虑由于天气随机变化影响运输效率的随机模型。在现实中，由于气候因素导致运输效率降低是相当普遍的，而在应急物流中，时效的重要性凸显，因此考虑天气随机因素的应急配送网络研究是有价值的。

二、问题描述

当某个地区遭受突发事件影响时，就需要对这个地区进行物资的应急配送。天气是对该地区进行应急配送重要的影响因素，它直接影响该物资运送的时间成本。当天气情况较好时，路段流量较为畅通，从而导致运输时间延长；反之，当天气情况较差时，路段流量较为拥堵，进而引起运输时间缩短。因此，天气状况对于整个交通运输有着重大影响，必须考虑天气随机变化情况下的应急配送中心选址和运输路线的安排问题。

灾害发生后，天气状况概率分布服从某种分布，其中x轴表示天气好坏，y轴表示天气状况的概率。当天气状况服从正态分布时，x的隶属函数的概率密度为：

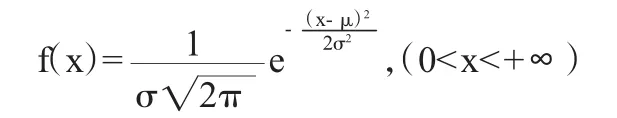
通过随机模拟，正是由天气状况和概率的随机取值来决定路段流量eij的随机分布，为了简化模型和便于求解，本文将路段流量eij的取值设定为服从0-1随机分布，分布如下：

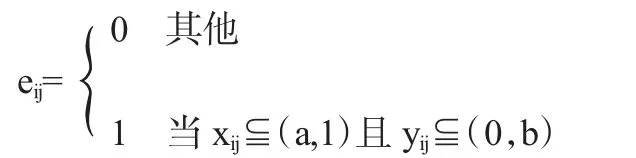
应急配送网络问题属于最小成本问题，其中不仅仅包括一般物流配送的费用成本，还包括时间成本。本文讨论的是多个受灾点和多个出救点的应急配送网络规划问题。其中主要包括两个问题，一个是出救点的选址问题，即在多个备选出救点中选取数量一定的点确定成为应急状况下的出救点，另一个是运输线路问题，即每个受灾点对应某个出救点进行物资的供应。该应急配送网络是以一个一级运输系统（即从出救点到受灾点之间的运输）运作总成本最小化为目标，综合考虑应急配送过程中的各种制约因素而建立的数学模型。

三、基本假设

1、模型假设

第一，假设天气变化服从某一正态分布。X-天气好坏的取值范围为（0，1），即x=0表示天气差，x=1表示天气好；Y- 概率的取值范围为（0，1），即y=0表示此状况发生的可能性为不可能，y=1表示此状况发生的可能性为一定发生。x表示一种对天气的评价好坏，y表示天气为x状况下的概率是多少。

第二，假设不同天气导致从出救点j到受灾点i的路段流量eij服从0-1随机分布。由于天气的变化，不同路段的流量eij随机变化。假设受灾点的数目是一定的，需求量的情况为随机需求。目前设成 xij取[a，1）且 yij取（0，b）上的值时，eij为 1，其它情况为0（a和b为可调参数，以免eij大部分为0）。

第三，备选的出救点已经过粗筛选，在确定的若干备选点进行选址，如果符合条件就建立，否则就不建立。

第四，出救点的容量、固定建设费用、物资的储存费用和运输成本均已知。出救点到受灾点的配送距离、单位运输费用和运输速度均已知。

第五，运输费用和运输量、距离成正比。出救点数目一定，且出救点有容量的限制。每个受灾点至少有一个出救点供货。目标函数为成本函数，且为线性函数。

2、符号与变量说明

第一，模型中的参数符号。

i：受灾点编号 i∈｛1，2，……I｝；

j：出救点编号 j∈｛1，2，……J｝；

eij：0-1变量，表示从出救点j到受灾点i的路段流量eij能否可行（1—可行，0—不可行）；

eij通过随机模拟的过程来掷筛子求出它的取值，每一段路都掷一次筛子；

E：最终选择的出救点j数量；

a：时间成本的权重a⊆（0.6，1）（使得时间作为主要的优化目标）（设定一个固定值，eg：0.6）；

fj：出救点j基础投资费用；

Lj：出救点j的最大容量限制；

Cj：出救点j的存储费用；

γi：受灾点 i的需求量；

Gij：出救点j到受灾点i的的单位距离运输费用（根据eij来确定，若eij=0，则为无穷大，否则由用户指定或由随机函数生成）；

dij：出救点j到受灾点i的距离；

vij：出救点j到受灾点i的运输速度；

第二，模型中的变量。

Mj：0-1变量，表示第j个待选出救点是否被选择建立（1—选，0—不选）；

Kij：0-1变量，表示出救点j和受灾点i是否存在供需关系（1—存在，0—不存在）；

Kij：救点j是否向受灾点i提供救助；

Xij：出救点j到受灾点i的运量。

四、模型的建立

应急配送网络问题属于总成本最小的问题，其中包括了时间成本和费用成本两大块。根据上述的模型假设，综合考虑了受灾点对物资的随机需求、给定出救点选址数量和出救点容量水平限制等情况，基于天气随机变化的以及配送网络模型的构建如下。

目标函数是：

对所建模型作简要说明：

目标函数（1）为应急配送网络的总成本最小，其中包括了时间成本和费用成本。其中函数（2）表示时间成本的最小化，函数（3）表示费用成本的最小化，即出救点开设和运营的固定建设费用，从出救点到受灾点的运输费用以及出救点物资的储存费用，物资在出救点和受灾点之间的选址配送等费用总和最小。

约束条件（4）保证允许开设的出救点的数目为确定量；约束条件（5）表示所有出救点i配送到受灾点j的商品总量要满足受灾点j对商品总需求量；约束条件（6）表示出救点的供应量是有限制的，出救点i配送到受灾点j的商品总量不得超过出救点的容量；约束条件（7）表示每个受灾点至少有一个选中的出救点供应物资；约束条件（8）表示非负变量的取值约束；约束条件（9）保证变量取0或1。

五、考虑天气随机变化的应急配送网络模型求解步骤

1、构造微粒表达方式

在应急配送网络模型的算法求解中，如何运用合适的微粒表达方法，是实现算法一个非常重要的突破点。应急配送网络出救点的选址问题主要是在一系列备选出救点中确定出救点的最佳位置，最终的目标是使总成本最小化。对于每个受灾点来说，就存在两个问题：是不是出救点，该受灾点隶属于哪个出救点。本文构造了一种微粒表达方法，对于一个H个受灾点的出救点的选址问题，每微粒对应于一个H列的矩阵。

例如，设某一应急配送网络有4个备选的出救点，要从中选出2个作为确定的出救点（即配送中心）；6个受灾点，若某微粒的位置向量X为：

出救点号：1 2 3 4

X1：0 1 0 2

受灾点号：1 2 3 4 5 6

X2：2 1 2 2 1 2

其中X1表示该备选的出救点是否为确定的出救点，0表示不是，自然数i表示在该点建立第i个出救点；X2表示该受灾点点隶属于第几个出救点。

在该例子中，配送中心为：2，4；需求点隶属情况为：

2：1，5

4：2，3，4，6

2、算法的求解具体步骤

线性递减惯性权重的粒子群算法求解考虑天气随机变化的应急配送网络模型，其算法总体流程如下：

Step1：设定微粒群算法参数。

Step2：初始化微粒 X。微粒 X 中：x=[M1，M2，…Mj]是（J+M）维二进制，wj∈｛0，1｝，1 表示网络节点出救点修建，0 表示不建。检查修建的出救点的总数是否满足设施设置的最小值约束，以及检验选中的出救点的处理能力是否能满足受灾点的需求，确保受灾点不会与未设置的出救点相关联。

Step3：初始化微粒eij。由天气状况符合正态分布或均匀分布，来确定eij的取值。若微粒eij=0，出救点j到受灾点i的单位距离运输费用Gij则为无穷大；若eij=1，则Gij=1。

Step4：评价每个微粒的适应值。以f目标函数，以其值最小为目标进行进化。

Step5：将当前各微粒的位置和适应值分别存储在各微粒的pi，fitmessi中，将所有pi中适应值最优个体的位置和适应值分别存储在 pg、fpbest中。

Step6：更新微粒的速度和位置。

Step7：更新微粒的权重。

Step8：执行Step3，评价每个微粒的适应值，并与fitnessi和fpbest进行比较，如果较好，则更新 fitnessi、fpbest、pi和 pg。

Step9：重复Step6到Step8给定的循环次数。

[1]唐康：基于随机需求的应急物资分配模型[J].现代商业，2010（8）.

[2]王世珍：多目标应急救援物资调度问题的研究[J].知识经济，2009（12）.

[3]李军军、王锡淮、黄有方、肖健梅：基于混合微粒群优化算法的配送中心选址问题求解[J].现代物流技术，2006（29）.

[4]Ayed Salmen，Imtiaz Ahmad，Sabah A1-Madani：Particle swarm optimization for task assignment problem[J].Microprocessors and Microsystems，2002（26）.

[5]汪定位、王俊伟：智能优化方法[M].高等教育出版社，2009.