考虑徐变影响的双面组合连续箱梁应力分析

李献泼， 段树金

(石家庄铁道大学 土木工程学院，河北 石家庄 050043)

0 引言

钢-混凝土双面组合连续箱梁同时吸收了箱梁结构和双面组合梁结构的优点。该结构形式主要由三部分构成:混凝土板，钢梁和剪力连接件，并且主要用于连续梁中［1］。整个连续梁在受力的过程当中存在正弯矩区和负弯矩区。正弯矩区中，结构的上部大部分受压，下部大部分受拉，考虑到这个特点，特将截面形式布置成如图1 所示。这种截面形式让混凝土充分发挥耐压的特点，承受弯曲压应力，增强梁的侧向稳定性，而让钢梁主要承受弯曲拉应力。在连续梁结构的负弯矩区中，结构的上部大部分受拉，而下部大部分受压，考虑到这个特点，将截面形式布置成如图2 所示。

图1 连续箱梁正弯矩区截面形式

图2 连续箱梁负弯矩区截面形式

根据组合梁由中不同区域的受力特点设置不同的材料，可最大程度地充分发挥混凝土和钢两种材料各自的优越性能［2］，这样不仅可以很好的满足结构的功能要求，而且还有很好的经济效益。但在结构的长期使用过程中，由于混凝土的徐变将会引起结构的应力重分布，因此在设计分析时必须考虑混凝土徐变的影响。

1 考虑徐变影响的双面组合连续箱梁应力分析

对于钢-混双面组合连续箱梁，在支座附近处的负弯矩区，上面的桥面板和钢梁受拉，下面的底板受压。以负弯矩区的截面为研究对象，进行分析时采用如下假定:(1)在长期荷载下，混凝土和钢梁都处于弹性工作状态;(2)混凝土的徐变与初始应变成比例;(3)不考虑普通钢筋;(4)不考虑滑移效应;(5)不考虑混凝土的受拉作用。建立图3 所示的简化分析模型。

在长期荷载作用期间，组合梁截面弯矩保持不变，因此有

式中，ΔMc为由徐变引起混凝土截面的附件弯矩;ΔMs为由徐变引起的钢梁截面的附件弯矩;ΔN 为附加轴力;d 为混凝土截面形心到钢梁截面形心之间的距离。

由混凝土徐变效应引起的截面附加曲率Δφ 为

式中，Ec为混凝土初始弹性模量;Es为钢梁的弹性模量;Ic为混凝土截面的惯性矩;Is为钢梁截面的惯性矩;φ 为徐变系数;χ 为龄期调整系数。

图3 双面组合箱梁负弯矩区截面分析模型

组合梁度底部混凝土截面下表面附加压应变Δεc和钢梁上缘附加拉应变Δεs分别为

式中，εc0为混凝土截面的初始应变;Ecl为混凝土的长期变形模量［3］;ys为钢梁的截面重心到钢梁下缘的距离。

从组合梁截面几何关系得到附加曲率的表达式

式中，h 为组合箱梁的截面高度。

从式(2)可以得到

将式(7)、(8)代入式(1)可以得到ΔN 的表达式

将式(3)、(4)、(7)、(8)、(9)代入式(6)整理得

令n1= n(1 + χφ)，n = Es/Ec，由文献［4］，且令，I01= Is+ Ic/n1，A01= AcAs/(Ac+ n1As)，A11=A01/(I01+A01d2)，则式(10)可以简化为

组合箱梁的初始曲率为

式中，EI 为组合箱梁的弹性换算截面刚度。因此组合箱梁的长期曲率为

混凝土的初始应变为

式中，y0为箱梁顶板混凝土上表面到中和轴的距离，经推导可得

所以式(13)可写为

根据不同的徐变系数的模型，可以选择不同的徐变系数φ 表达式，代入(17)式，就可以得到组合箱梁在考虑徐变效应的长期曲率。从而得到:

箱梁顶板上表面应力为

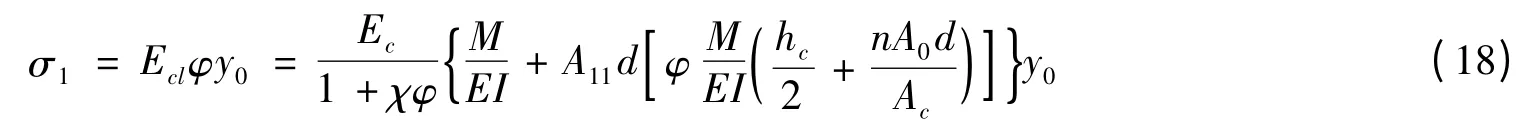
钢梁上缘应力

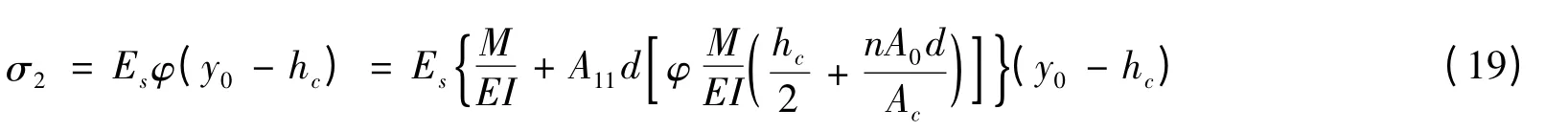
箱梁底板下表面应力

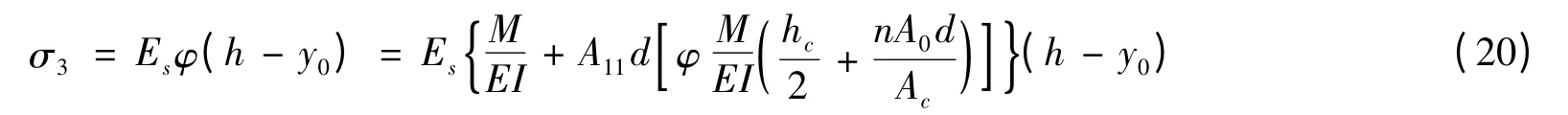
2 算例分析

建立三跨双面组合连续箱梁，总长150 m，跨径布置为(45 +60 +45)m，箱梁顶板为混凝土，宽6 000 mm，厚300 mm;腹板为工字形钢梁，高为1 750 mm，翼板宽300 mm，厚度为25 mm，两腹板形心间距为3 m;底板在正弯矩区为钢板，厚度为25 mm，在负弯矩区为混凝土板，板厚为250 mm;上下混凝土板都是采用的C50 混凝土材料，主梁是采用的Q345 的钢材;徐变函数是采用JTG D62—2004 规范。通过模型仿真计算，得到钢-混双面组合连续箱梁沿梁纵向坐标方向的应力变化。

在荷载的长期作用下，钢-混双面组合梁中的混凝土徐变，会引起截面应力的重分布。从图4 至图6 可以看出，由于混凝土的徐变作用，双面组合梁桥面板发生了一定作用的卸载作用，应力减小，而钢梁由于承受了桥面板转移的的一部分应力，所以应力增大。桥面板上表面应力压应力减小的最大截面在第二跨的跨中截面，应力从成桥初期的5．51 MPa 变化为成桥10 a 后的4．53 MPa，减小了17．8%;钢梁上缘压应力变化最大的也发生在第二跨的跨中截面，成桥初期为54．85 MPa，成桥10 a 后为75．1 MPa，增大了36．9%。从图6 中看到，箱梁底板下表面在负弯矩区由于混凝土在徐变的作用下也有一定的卸载，压应力从成桥初期时的11．9 MPa 到成桥10 a 后的9．34 MPa，减小为21．5%，在正弯矩区应力有所增加。

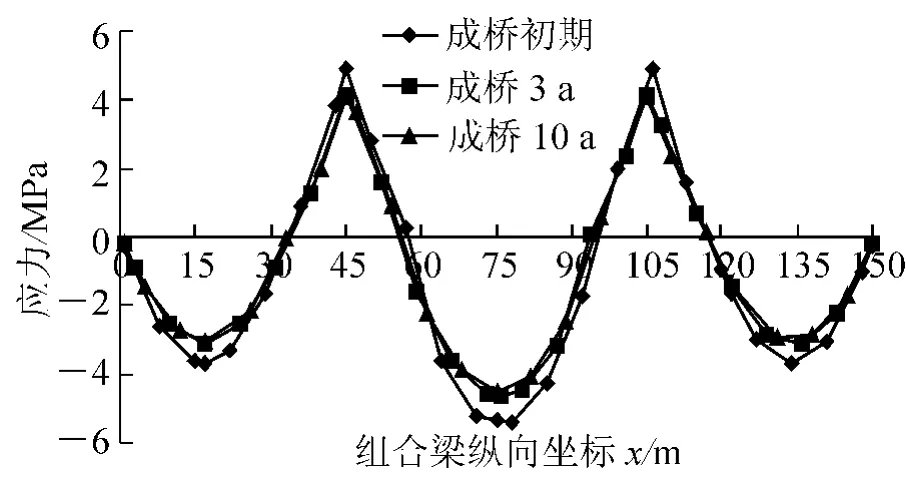
图4 箱梁顶板上表面徐变应力

图5 徐变引起钢梁上缘应力变化

图6 箱梁底板下表面徐变应力分布

3 结语

根据本文所建的组合箱梁应力公式，可以计算不同徐变系数的截面应力。对算例的计算结果进行分析，双面组合箱梁的各个部分的应力随着时间的变化都有不同程度的变化，徐变作用使桥面板得到一定程度的卸载，将一部分的应力转移到钢梁，使混凝土桥面板的压应力减小，钢梁的应力增大，因此在结构的设计过程中要准确的考虑混凝土的徐变作用。论文中的模型建立没有考虑到收缩、温度、滑移等因素的影响，因此还需进一步的研究。

［1］郑浩，段树金．钢-混凝土组合箱梁力学分析［J］．石家庄铁道学院学报:自然科学版，2009，22(2):11-14．

［2］王连广．钢与混凝土组合结构理论与计算［M］．北京:科学出版社，2005:1-9．

［3］聂建国．钢-混凝土组合梁强度、变形和裂缝的研究［J］．清华大学学报:自然科学版，1994(2):8-12．

［4］聂建国，沈聚敏．钢筋混凝土梁在长期荷载作用下的变形［J］．建筑结构学报，1996，13(3):3-9．