重载列车作用下铁路钢桁梁桥的动力响应分析及疲劳寿命评估

李运生， 安立朋， 魏树林， 张德莹

(1．石家庄铁道大学 土木工程分院，河北 石家庄 050043;2．石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室，河北 石家庄 050043;3．华东交通大学 土木建筑学院，江西 南昌 330013;4．郑州铁路局 公务检测所，河南 郑州 450052)

0 引言

随着我国经济的快速发展，铁路运输的压力越来越大，在既有线上开行重载列车以增加运力的措施已经展开，但同时会加重既有线桥梁的疲劳损伤，缩短其使用寿命。因此，保证重载车辆作用下既有线桥梁的安全性，对其疲劳寿命进行评估，显得至关重要。

关于钢桥的动力及疲劳性能分析方面已有一些报道。Xia H et al［1］对车-桥耦合动力分析在钢桥加固中的应用进行了研究;孙颖 等［2］对既有铁路钢桁梁桥动力特性及横向刚度的加固问题进行了研究;G．Kaliyaperumal et al［3］对斜铁路钢桥进行了高等动力有限元分析;郭薇薇 等［4］对铁路新型钢-混凝土组合桁架桥在列车作用下的动力响应进行了分析;彭修乾 等［5］对重载既有线路桥过渡段的动力响应特性进行了分析;Zhao Zhengwei et al［6］对基于可靠度的钢桥疲劳评估进行了研究;Mohammad．J et al［7］对基于现场实测的桥梁疲劳寿命评估方法进行了研究。以上文献大多是对钢桥在普通车辆荷载下的动力特性进行分析，涉及铁路重载作用的较少。

以长东黄河大桥三跨铁路连续钢桁梁为工程背景，采用ANSYS 软件建立了有限元模型，首先对其自振特性进行了分析，然后对C64K 型、C70 型和C80 型三种不同载重列车车辆过桥时钢桁梁的动力响应进行了分析，并对C80 重载列车过桥时钢桁梁的疲劳损伤度及疲劳寿命进行了评估。

1 钢桁梁的有限元模型及自振特性

长东黄河大桥是新菏线跨黄河的一座特大桥，上行线主跨自东向西为9 ×96 m 简支钢桁梁+4 ×108 m 连续钢桁梁+3 ×108 m 连续钢桁梁组成，本文针对其中的3 ×108 m 连续钢桁梁进行分析。钢桁梁由两片主桁、上下平纵联和横联组成。主桁高16 m，宽5．75 m，节间长12 m。钢桁梁均采用工字型截面，材料为16Mnq 钢。主桁立面图见图1 所示。

图1 长东黄河大桥是钢桁梁主桁立面图(单位:m)

采用ANSYS 软件进行建模，结构杆件单元采用BEAM44 单元，不考虑节点板刚度不足的影响，单元间连接全部为刚接;结构杆件截面为工字型钢，根据设计图纸尺寸采用自定义截面的方法输入截面特性;节点E0、E18、E0＇为活动铰支座，约束Y、Z 方向的平动自由度，节点E18＇为固定支座，约束X、Y、Z 方向的平动自由度。由ANSYS 软件计算得到钢桁梁模型的自振特性。钢桁梁的有限元模型及前5 阶自振频率和振型见图2 所示。

图2 有限元模型及前5 阶振型

从图2 钢桁梁桥自振特性的计算结果可以看出，钢桁梁前三阶振型以横向弯曲为主，竖向振动不明显，第四阶、第五阶振型以扭转振动为主，有少量竖向弯曲，出现在边跨跨中位置。说明该钢桁梁的竖向刚度比横向刚度要强。

2 车桥动力响应分析

2．1 列车荷载模型

长东黄河大桥所在的新菏线主要运营C64K 型通用敞车和C70(C70H)型通用敞车，考虑运量的发展，还计划运营C80 型铝合金运煤敞车，三种车辆载质量不同，各车详细参数如表1 所示。

表1 三种不同型号车辆参数

在车桥动力分析中，移动车辆的简化有多种模型，主要包括移动荷载、移动质量、移动简谐力和移动簧上质量。其中，采用移动簧上质量最合理，但也最为复杂，较简单的方法是采用移动荷载和移动质量模拟车辆过桥。文献［8］分别采用移动荷载和移动质量进行了桥梁的动力响应分析，发现两种方法差别不大，都能较准确地模拟移动车辆的响应，因此采用移动荷载法模拟列车一次过桥时结构的动力响应，并分析不同车辆作用下钢桁梁桥动力响应的差别。

在ANSYS 模型中，用节点集中力模拟列车轮对的荷载，建立有限元模型，如图3 所示。图3 中，车辆质量平均分配在八个集中力上，每个车轮的集中力大小为F。

图3 车桥模型

2．2 动力响应结果

长东黄河大桥设计速度100 km/h，现在运营速度为100 km/h。采用上述钢桁梁模型和车辆模型，计算车桥动力响应。模拟三种车辆以100 km/h 速度过桥时桥梁的动力响应，得到钢桁梁左跨跨中下弦杆E8E10 的竖向动挠度、竖向加速度时程曲线和下弦杆轴向应力时程曲线，如图4 ～图6 所示。图中车辆位置表示机车最前侧车轮位置。以下分析图中均以刚桁梁桥的起点为坐标原点，故当横坐标L =0 m 时，机车上桥;L =324 m 时，机车出桥。

图4 三种车辆过桥引起边跨跨中下弦节点竖向动挠度

图5 三种车辆过桥引起边跨跨中下弦杆轴向应力

由图4 ～图6 可知:

(1)C64K、C70、C80 三种车辆以100 km/h 速度过桥时，节点E10 的最大动挠度和下弦杆E8E10 的最大轴向应力均发生在车辆行驶到边跨跨中位置时，最大动挠度分别为48．421 mm、49．467 mm、50．525 mm，轴向应力极值分别为40．062 MPa、40．942 MPa、41．816 MPa，说明二者均随车辆轴重的增加而加大。

(2)最大加速度响应发生在车辆刚进入桥梁至四分之一跨径时，竖向加速度极值分别为4．056 m/s2、4．772 m/s2、2．293 m/s2，加速度值和车辆轴重不成正比，不严格随着轴重的增加增大或减小。

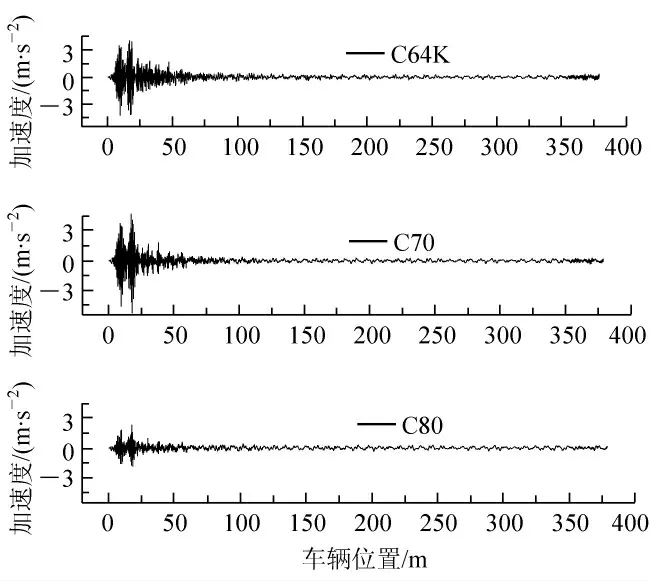
图6 三种车辆过桥引起边跨跨中下弦节点竖向加速度

计算C80 车辆以不同速度过桥时，结构的动力响应情况。模拟车辆分别以50 km/h、80 km/h、100 km/h 速度过桥，得到边跨跨中下弦节点E10 的竖向动挠度、竖向加速度和边跨跨中下弦杆E8E10 的轴向应力如图7 ～图9 所示。

由图7 ～图9 可知:

(1)C80 车辆以50 km/h、80 km/h、100 km/h 速度过桥时，引起的边跨跨中下弦节点E10 的竖向动挠度极值分别为50．354 mm、50．377 mm、50．525 mm;边跨跨中下弦杆E8E10 的轴向应力极值分别为41．46 MPa、41．553 MPa、41．816 MPa。可见由于结构刚度较大，在低速范围内车辆的动力作用不明显，结构动挠度和轴向应力极值随着车辆速度的增加变化不大，但波动幅度随车速的增加而增大。

图7 C80 车辆以不同速度过桥时引起的边跨跨中下弦节点竖向动挠度

图8 C80 车辆以不同速度过桥时引起的边跨跨中下弦杆轴向应力

(2)竖向加速度极值分别为0．546 m/s2、1．542 m/s2、2．293 m/s2，随着车速的增加而增大。

3 C80 车辆荷载作用下钢桁梁疲劳损伤及寿命评估

下面讨论在列车荷载作用下钢桁梁的疲劳损伤及寿命评估。疲劳损伤度D 的计算采用式(1)所示的线性疲劳累积损伤理论完成。

式中，ni为对应于应力幅水平σi的加载循环次数，Ni为对应于应力幅水平σi的疲劳破坏次数。当各级应力对材料的总损伤值D 达到1．0 时，材料就会发生破坏。

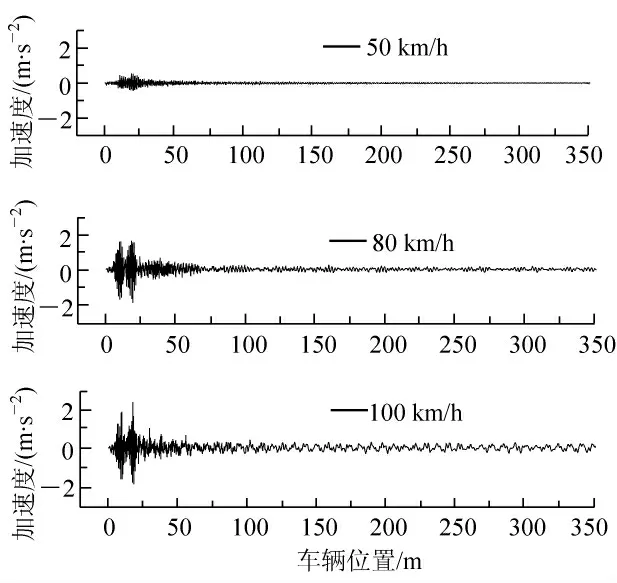
图9 C80 车辆以不同速度过桥时引起的边跨跨中下弦节点竖向加速度

在分析C80 车辆过桥时钢桁梁桥的疲劳特性时，采用雨流法对应力时程曲线进行应力幅的分级和统计计数。钢材的疲劳曲线按《钢结构设计规范》(GB 50017—2003)取用

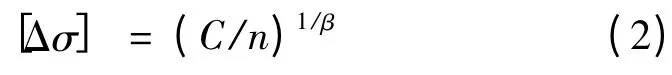
式中，n 为应力循环次数;C、β 为参数，根据构件和连接类别确定;Δσ 为常幅疲劳的容许应力幅。

3．1 最不利列车编组形式下控制杆件的应力时程曲线

长东黄河大桥的主桁杆件截面尺寸不同，列车通过桥段时荷载工况不断变化，在不同时刻，最大应力杆件会在不同位置。通过对各控制截面的对比分析，得出在大部分工况下，边跨跨中下弦杆的拉应力基本都能达到最大，故选取下弦杆E8E10 为控制杆件，计算列车过桥时该杆件的轴向应力时程曲线。

根据新菏线列车运营条件，桥上运营列车最重为C80 车辆，根据机车牵引定数，选取最不利列车编组形式，模拟两台东风4 机车牵引38 辆C80 车厢以100 km/h 速度过桥，得到钢桁梁边跨跨中下弦杆E8E10的应力时程曲线如图10 所示。

图10 中，0 m 时列车开始上桥，324 m 时列车布满桥跨开始出桥，897．3 m 时列车全部驶出桥梁。由图10 可知，列车自上桥始，边跨跨中下弦杆E8E10 的轴向应力逐渐增大，在102．2 m 列车布满边跨时达到极大值;然后随着列车前进，应力值逐渐减小;在209．2 m 至534．6 m 之间，列车布满桥梁，应力进入平缓段，之后列车尾部车厢开始驶离左边跨端部，即234#支座位置，应力值开始减小，在643．4 m 时减小到极小值，此时列车尾部车厢大约行驶至235#支座处，连续梁中间跨荷载开始减少，边跨下弦杆应力出现反弹，到744．8 m 时达到极大值，此时列车尾部车厢大约行驶至236#支座处，随着列车继续往前，边跨下弦杆应力少量减小后，在30．956 MPa 上下波动，897．3 m 时列车全部驶出桥梁。

3．2 钢桁梁疲劳损伤度及寿命评估

铁路桥梁的实际疲劳寿命总是比理论评估值小，原因主要是应力集中或缺陷造成的。考虑钢桁梁螺栓连接处栓孔位置在拉伸下的应力集中系数，查应力集中系数手册取为1．424。用雨流法提取应力谱，得到C80 编组列车过桥时名义应力谱如表2 所示。

表2 C80 编组列车以100 km/h 速度过桥时引起的边跨跨中下弦杆应力谱

根据Miner 线性累计损伤理论和表2 应力谱计数结果，按照公式(1)，计算得到模拟编组列车通过钢桁梁桥时，引起的钢桁梁桥边跨跨中下弦杆疲劳损伤度为:

经初步统计，根据当前桥梁运营状况调查，按每个列车编组约60 辆货车，每昼夜运营约70 个编组，由此可得该钢桁梁在C80 列车编组作用下的疲劳寿命约为125 a。采用同样方法对C70 列车编组和C64K列车编组作用下该钢桁梁的疲劳寿命进行计算，结果为C70 编组下130 a，C64K 编组下529 a。说明该桥在现有列车运营情况下疲劳寿命满足设计要求。虽然C80 车辆比C70 轴重大，但轴间距也较大，因此在两种列车编组下该钢桁梁的疲劳寿命相差不大。

4 结论

通过对长东黄河大桥三跨连续钢桁梁在不同列车荷载作用下的动力响应分析，得到如下主要结论:

(1)列车车辆过桥时，三跨连续钢桁梁边跨跨中的最大动挠度响应发生在车辆前端行驶到该位置时，且随车辆轴重的增加而加大;最大加速度响应发生在车辆刚进入桥梁至四分之一跨径时，加速度值不严格随着轴重的增加增大或减小。

(2)在低速范围内车辆的动力作用不明显，结构动挠度极值随着车辆速度的增加变化不大，但波动幅度随车速的增加而增大;竖向加速度极值则随着车速的增加而增大。

(3)长东黄河大桥三跨连续钢桁梁在现有列车运营情况下疲劳寿命满足设计要求，C80 列车编组下的疲劳寿命约125 a，与C70 列车编组下的疲劳寿命相差不大。

［1］Xia H，De Rocek G，Zhang H R，et al． Dynamic analysis of train-bridge system and its application in steel girder reinforcement［J］．Computers ＆ Structures，2001，79:1851-1860．

［2］孙颖，顾萍． 既有铁路钢桁梁桥动力特性及横向刚度加固研究［J］．石家庄铁道学院学报，2007，20(1):10-13．

［3］Kaliyaperumal G，Imam B，Righiniotis T．Advanced dynamic finite element analysis of a skew steel railway bridge［J］．Engineering Structures，2011，33(1):181-190．

［4］郭薇薇，夏禾，李慧乐，等． 铁路新型钢-混凝土组合桁架桥在列车作用下的动力响应分析［J］．振动与冲击，2012，31(4):128-133．

［5］彭修乾，时瑾． 重载既有线路桥过渡段动力响应特性分析［J］．铁道科学与工程学报，2011，8(4):7-13．

［6］Zhao Zhengwei，Achintya Halder，Florence L Breenjr． Fatigue-reliability evaluation of steel bridge［J］．Journal of Structural Engineering，1994，120:1608-1623．

［7］Mohammad J，Guralnick S，Polepeddi R． Bridge fatigue life estimation from fiele data［J］．Practice Periondical on Structural Design and Construction，1998，23:128-133．

［8］Liu K，Reynders E，DeRoeck G，et al． Experimental and numerical analysis of a composite bridge for high-speed trains［J］．Journal of Sound and Vibration，2009，320:201-220．