基于传感器网络的多目标跟踪和特征管理方法

王鼎元，邸 兴，党小宝

（中国飞行试验研究院 陕西 西安 710089）

近来传感器技术和无线通信技术的发展导致了一个新概念的诞生－传感器网络，即一个由本地传感器节点所组成的具有感知、处理和通信能力的一种广泛应用的网络[1]。为了更深入地挖掘传感器网络所具有的能力，笔者提出了一种可扩展分布式的多目标跟踪和特征管理方法，该方法能够通过一个传感器网络对多个目标实现跟踪和特征管理。

传统的多目标跟踪方法，如MHT跟踪器[2]，不适用于传感器网络。而现有基于传感器网络的算法[3]仅基于如下情况：所跟踪目标的数量已知不变，并且它们的运动轨迹对于本地传感器已知。而在本文中，笔者放宽了以上假设，形成对于分布式多目标的跟踪和特征管理算法DMTIM。文中在实现数据关联和多目标跟踪运用了马尔科夫链蒙特卡罗数据关联MCMCDA[4]的方法，实时对未知数量的多目标进行跟踪。MCMCDA方法能够独立地对轨迹进行起始和终止，并能够跟踪未知数量的多目标。每个传感器能够运用MCMCDA有效地跟踪一组未知数量的目标，并且能够对目标的特征进行分布式地管理。

本文结构如下：分布式多目标的跟踪与特征管理算法概述；多目标跟踪问题及其概率模型；DMTIM关键算法叙述：马尔科夫链蒙特卡罗数据关联算法；DMTIM组成部分介绍，包括数据关联、多目标跟踪、特征管理和信息融合；DMTIM算法仿真试验及评估。

1 分布式多目标跟踪和特征管理

文中研究重点是传感器网络中多目标的跟踪和特征管理方法。每个传感器拥有自己的观测区域，且拥有与其邻近传感器通信的能力。如图1所示一个简单的二传感器的系统，大圆圈代表传感器的观测区域。每个传感器能够对多目标进行跟踪并在观测区域内管理目标特征。该问题的难点在于观测区域内目标的数量会随时间而变化，因此我们必须寻求一种可扩展的，在相邻传感器中具有本地一致性的方法。

图1 传感器网络示意图Fig.1 Sensor network

笔者提出的可扩展的分布式多目标跟踪与特征管理DMTIM算法能对未知数量且数量随时变化的机动目标进行跟踪，对其特征进行有效的管理。并能够在一个分布式的传感器网络中进行实现。对于每一个传感器，DMTIM中的多目标跟踪算法负责估算如下量：目标的数量，观测区域内所有目标的运动轨迹，以及在特征管理算法中将用到的混合矩阵和本地信息。然后，相邻的传感器通过相互通信对本地状态估算值和信任矩阵进行交换。同时，通过信息融合实现了本地一致性，进而实现全局一致性。

本文的剩余部分对DMTIM的算法模块进行了详细描述。并且还对多目标跟踪问题，以及马尔科夫链蒙特卡洛数据关联进行了描述。

2 多目标跟踪

基于每个传感器视野范围内的目标数量会随时间不断变化，本章提出的DMTIM多目标跟踪适应于此类多目标数量不确定的情况。

2.1 问题模式

设T∈Z+为传感器观测持续的时间，K为该时间内观测范围 R中所出现的目标数量。在某时间段[tki，tkf]⊂[1，T]内，每一个目标都在R范围内移动，K和{tki，tkf}的值未知。每个目标都是在某时间点tki随机出现在R范围内，直到在时间点tkf时消失。对于每个时间点，目标保持其存在的概率为1-pz，消失的概率为pz。对于每一个时间点，在R范围内所出现目标的数量都具有一个位置分布，该位置分布包含参数λbV，其中λb表示单位时间单位范围内的出现率，V表示观测范围R的大小。并特定每个新目标的初始位置都在R范围内。

设FkRns→Rns为目标k的离散时间运动，其中nx是状态变化的维度。并设xk（t）∈Rns为时刻t目标k的状态。目标t的运动服从公式（1）：

其中 ωk（t）∈Rns属于白噪声过程，包含在了目标非直线运动模型。并运用一个探测概率pd来计算目标状态的噪声。目标不被发现并被视为跟踪丢失的概率为1-pd。本文设定了错误报警，其数量也遵循含有参数λfV的位置分布，其中λf是单位观测范围单位时间内的错误报警率。设n（t）为时间点t观测点的数量，该数量包括了噪声观测和错误报警。设yj（t）∈Rny为时间点t的第j个观测值，其中ny是每一个观测向量的维度。每个被测物体都会在该采样时间产生一个特定的观测值，如公式（2）所示，其中 Hj:Rnx→Rny为观测值模型。

其中 vj（t）∈Rnyvj（t）是白噪声过程，u（t）是错误报警的随机过程。目标是观测目标类型或属性信息，状态变量可以扩展到包括目标类型的信息。因此多目标识别的问题即是从观测值中计算出 K、{tki，tkf}、{xk（t）:tki≤t≤tkf}，其中 k=1，…，K。

2.2 多目标跟踪方法

设 y（t）={yj（t）:j=1，…，n（t）}为时间 t的所有值，Y={y（t）:1≤t≤T}为时间t=1到t=T的所有计算值。设Ω为所有Y的集合，且ω∈Ω，有如下参数：

1）ω∈{τ0，τ1，…，τK}

2）∪Kk=0τk=Y，且 τi∩τj=Ø，i≠j；

3）τ0为错误报警的集合；

4）|τk∩y（t）|≤1，k=1，…，K，t=1，…，T；

5）|τk|≥2，k=1，…，K.

分离的过程如图2所示，其中K为轨迹数量，|τk|为 τk的基数，当没有轨迹互扰的情况下认为τk为一个正确的轨迹。假设一条轨迹至少包含两个观测值，因为不能由一个单一的观察值确定一条轨迹。于是再假设e（t-1）为时刻t-1之后目标的数量，z（t）为时刻 t消失的目标的数量，c（t）=e（t-1）-z（t）为时刻t-1到t未消失的数量。设a（t）为时刻t新出现的目标，d（t）为时刻 t的实际目标，g（t）=c（t）+a（t）-d（t）为未识别的目标。 最后，设 f（t）=n（t）-d（t）为错误报警数量，有：

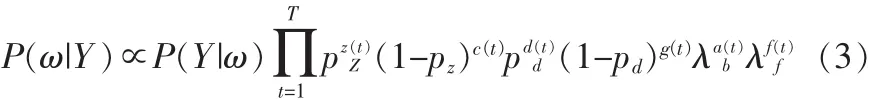
其中P（ω|Y）是Y的相似概率。

图2 轨迹分离示例图Fig.2 Example of tracks’partition

本文采用了最大后验MAP算法解决多目标跟踪问题。该算法对观测目标进行分割，并根据分割对目标状态进行估算。

3 马尔科夫链蒙特卡洛数据融合

本节提出一种解决第二节中多目标跟踪问题的算法，该算法是离散多目标跟踪与识别算法模块的核心。

3.1 马尔科夫链蒙特卡洛模型

马尔科夫链蒙特卡洛模型是已知唯一能在多项式时间复杂问题下实现估值计算的方法，同时，还是一种从位于空间Ω的分布π中提取抽样值的普遍方法，该方法通过状态值ω∈Ω和稳定分布值π（ω）建立的马尔科夫链M来实现其算法。现在来描述该算法。在状态ω∈Ω，假设ω′∈Ω服从分布q（ω，ω′）。 而运动的感知服从感知概率 A（ω，ω′），其中：

然而样本保持在ω。通过计算，平衡条件得以满足，例如，对于所有的ω：

其中，P（ω，ω′）=q（ω，ω′）A（ω，ω′）是从 ω 到 ω′的跃迁概率。

如果M具约束性和非周期性，并且M由遍历定理收敛至均匀分布[5]。因此，对于一个给定的有界函数f:Ω→Rm，样（ω）收敛于 N→∞。 可以注意到公式（4）只需计算出 π（ω′）/π（ω）的比值，而无需对π进行标准化。

3.2 马尔科夫链蒙特卡洛数据关联

MCMCDA算法是马尔科夫链蒙特卡洛算法的特殊形式，其状态空间是上文在第2.2节中提到的，并且其平稳分布服从公式（3）。对于MCMCDA的分布有5类动作组成。它们包括：1）发现∕消失运动；2）分割∕合并运动；3）扩展∕减少运动；4）跟踪刷新运动；5）跟踪切换运动。

MCMCDA的运动方式如图3中所示，每个运动的详细描述[6]在此省略。MCMCDA的输入是一系列观测值Y，样本观测值的个数nmc，初始状态ωinit，以及有界函数X:Ω→Rm。对于该算法的每一步，ω是马尔科夫链的当前状态。其获取概率A（ω，ω′）如公式（4），输出X^接近 MMSE 的估计值 EπX，且ω^接近MAP 的估计值 arg max P（ω|Y）。

4 分布式多目标跟踪与特征管理算法结构

现在对分布式多目标跟踪与特征管理算法进行详细描述。运用一种信念向量来表示目标的特征。对于多目标的情况下，我们需要运用信念矩阵 B（t），其各列由信念向量 Bij（t）所组成。因此，向量表示目标j能被t时刻的i所确定的概率。

4.1 多目标跟踪（数据关联）

DMTIM多目标跟踪（数据关联）模块的输出涉及到混合矩阵、状态估计值和本地信息三者的计算。

首先需要求得混合矩阵。假设在观测范围内有K个目标具有K个特征，因此特征管理意味着对多目标的特征进行匹配。对此，运用Identity-Mass-Flow[7]的方法。混合矩阵是一个K×K矩阵，其元素 Mij（t）表示目标 i在t-1时刻变成目标 j的概率。而MCMCDA能够在多项式时间下对混合矩阵进行有效地估算。

图3 马尔科夫链蒙特卡洛数据关联示意图Fig.3 Graphical illustration of MCMCDA

然后需要对状态估计值进行计算。如上所述，MCMCDA能够对未知数量的多目标进行跟踪，并且能够实现轨迹的发生与终止。在每一个采样时间段，其测量值与前一段的测量值相叠加，从而构造出测量值集合Y。MCMCDA能求出ω^，其值接近多目标跟踪的MAP估计值，以及ω^中所有轨迹的状态估计值。对于每一个轨迹τ∈ω，将它与之前发现的目标轨迹进行比较。如果τ与之前目标轨迹的测量值无任何相同之处，那么我们认定其为新目标。然后，当前传感器τ对于对相邻传感器进行询问，如果相邻传感器对τ已知，那么它的特征将被复制到当前传感器当中。否则，将对τ创建新的特征。最后，当轨迹结束时，对目标特征进行删除。在第4.2节，将对目标数量变化情况下信任矩阵如何实现刷新进行描述。

最后计算表示为信任向量的形式的本地信息。MCMCDA方法能够通过最新的，以及之前的测量值有效地计算出本地信息。当目标和轨迹的数量处于估计值的情况下，本地信息能够被同时计算出来。对于特征值k，定义Njk为时间点个数，第j个最新观测值与之前的观测值合并，观测值在之前的nbi个采样值中由k表征，其中nbi为之前的采样值数量。算法结束时对特征值 k 计算。 然后根据最新的观测值来对向量进行调整，进而通过γk来形成本地信息。

4.2 特征管理

特征管理模块包括信任矩阵刷新和本地信息关联，而多目标跟踪（数据关联）的混合矩阵和本地信息被用来刷新信任矩阵。

信任矩阵刷新模块包含存储在K×K信任矩阵B（t）中的特征信息。信任矩阵的刷新如下：

可以看出，公式（6）使信任矩阵行、列之和保持不变。然而目标数量的变化使该方法不适用于分布式特征管理。数量的变化有两种情形：目标离开和进入观测区域。目标离开，对传感器中混合矩阵的相应列进行删除；目标进入，又有两种情形：1）目标从相邻传感器区域进入，2）目标从未知区域进入。

而本地信息被运用来降低由香农信息所得的信任矩阵的不确定性。L×K信任矩阵的香农信息定义如下：

接下来的问题是将该信息关联到信任矩阵。信任矩阵具有如下性质：各列之和等于1；各行之后保持不变；各列之和的和与各列之和的和相等。如果将某列替换为本地信息，将无法保证以上性质。当且仅当本地信息能够降低信任矩阵的不确定性时才能与信任矩阵进行关联。

4.3 信息融合

DMTIM算法通过信息融合来计算本地传感器网络的全局信息，具体包括来自不同传感器的状态估计值和特征信任向量的融合。

特征信息 （信任向量）的融合能够被表述为最优化的问题。3个不同的成本函数，香农信息（Shannon information），切尔洛夫信息 （Chernoff information）， 以及莱布勒距离（Kullback-Leibler distances）之和代表了不同的性能指标。本文场景[8]中所有的传感器都参与协同工作，因此我们采用香农信息的方法。

鉴于每个目标可能具有来自不同传感器的多重轨迹，运用轨迹数据融合方法[9]来对多重的轨迹进行合并。设ωi为来自传感器i的轨迹，NBi为包括i并与i相邻的一系列传感器。 设 Y′={τk（t）:τk∈ωj，1≤t≤T，1≤k≤ω|ωj|，j∈NBi}为所有确定目标的一系列观测结果。通过重叠观测区域，可以由Y′得到一系列合并观测结果Y。于是得到一系列新的轨迹ωinit。然后对一系列合并观测结果运行算法，以得出本地稳定的跟踪轨迹，其初始状态为ωinit。

5 仿真结果

在该节中，提供一个简单的场景来说明DMTIM算法的性能。环境中有两个固定传感器—空中交通管制雷达，在二维空间中对多架飞机进行跟踪。假定每个传感器观测范围的半径为10 km，并且当两传感器距离进入20 km的通信范围，它们之间可以实现相互通信。该场景中包含3架飞机，如图4所示。被标注为A和B的飞机首先被预注册，被标注为的飞机对于特征管理系统是未知的。左侧传感器被传感器1所标注，右侧传感器被传感器2所标注。每个传感器中的多目标跟踪模块对目标的数量进行估算，并且对每个已知目标的轨迹进行估算。在图5中，目标数量改变的事件被垂直的点线所标注。在时刻1，传感器1感知到目标1，并且其信任向量为（）T=（0.8，0.2）T，其中 bij，k是目标 k 能够被传感器 i所感知并标定为j的概率；同时传感器2感知到它的目标1，并且其信任向量为（）T=（0.2，0.8）T。 在时刻 9，传感器1发现新目标（传感器1的目标2），并赋予新值X。同时，传感器2感知到新目标（传感器2的目标2），该目标的特征值和状态估计信息从传感器1转移过来。以此类推，在时刻30，传感器2的目标2离开了传感器2的观测范围，其信息随机从传感器2删除。

信息融合能够降低目标交叉运动所产生的不确定性。鉴于香农信息效率的优越性，在该试验中我们运用了该方法来实现信息的融合。图6所示为融合的信任向量，图7为实现状态估计融合后各传感器所估算的轨迹。

图4 三飞机、双传感器系统Fig.4 System of three-aircraft，two-sensor scenario

图5 传感器对目标数量的估计值Fig.5 Estimated number of targets by each sensor

图6 融合处理后的信任向量Fig.6 Fused belief vector

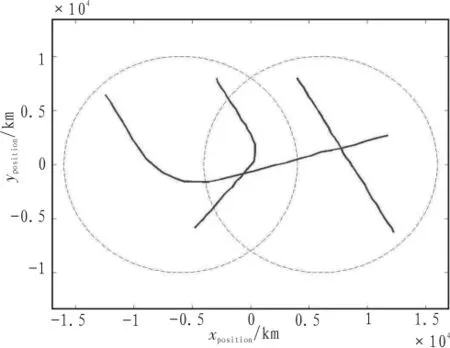
图7 融合算法后的轨迹Fig.7 Fused tracks

6 结 论

笔者主要对传感器网络下多目标的跟踪和特征管理方法进行了研究。数据关联和多目标跟踪的问题能够由马尔科夫链蒙特卡洛数据关联算法有效地解决，该算法能够对数量未知且数量随时间变化的多目标进行跟踪。文中还讲述了一个可扩展的分布式多目标跟踪和身份管理（DMTIM）算法，该算法能够对多目标进行跟踪，并在分布式传感器网络环境下能够有效地管理目标的特征。DMTIM算法由数据关联，多目标跟踪，特征管理，以及信息融合四部分所组成。DMTIM能够对某目标特征的本地信息进行有效地整合，以降低系统的不确定性，并通过信息融合来保持相邻传感器的本地一致性。

[1]Cayirci A.Asurveyonsensornetworks[J].IEEECommunications Magazine，2002，40（8）:102-114.

[2]Reid D.An algorithm for tracking multiple targets[J].IEEE Transaction on Automatic Control，1979，24（6）:843-854.

[3]Hwang I，Balakrishnan H，Roy K，et al， Tomlin.Multiple-Target Tracking and Identity Management Algorithm In clutter[C]//Proceedings of the AACC American Control Conference， Boston，2004:18-20.

[4]Ohs， Russells， Sastrys.Markov Chain Monte Carlo Data Association for Multiple-Target Tracking[J].Tech.Rep，2005，23（5）:45-49.

[5]Roberts G..Markov chain concepts related to sampling algorithms[J].Markov Chain Monte Carlo in Practice，1996:256-267.

[6]Ohs， Russells， Sastrys.Markov Chain Monte Carlo Data Association for General Multiple-Target Tracking Problems[C]//the 43rd IEEE Conference on Decision and Control， 2004，6（3）:12-23.

[7]Shin J， Guibas L J， Zhao F.A distributed algorithm for managing multi-target identities in wireless ad-hoc sensor networks[J].Information Processing in Sensor Networks，2003:223-238.

[8]Hwang I， Roy K， Tomlin C.A Distributed Multiple-Target Identity Management Algorithm in Sensor Networks[C]//the 43nd IEEE Conference on Decision and Control，2004，3（7）:34-39.

[9]Ohs， Schenatos， Sastrys.A Hierarchical Multiple-Target Tracking Algorithm for Sensor Networks[C]//the International Conference on Robotics and Automation，2005:8（2）:12-16.