基于谱系聚类的随机子空间模态参数自动识别

汤宝平，章国稳，陈 卓

（1.重庆大学 机械传动国家重点实验室，重庆 400030；2.重庆交通科研设计研究院 桥梁结构动力学国家重点实验室，重庆 400067）

随机子空间方法（SSI）［1-2］是近年来发展起来的一种行之有效的环境激励模态参数识别方法，该方法直接工作于时域数据，没有频率分辨率误差的问题，不但能准确识别系统的频率，而且能很好的识别系统的模态振型和阻尼。在识别过程中结构模型的定阶是最关键的环节之一，常见的做法是先对系统阶次进行过估计，然后结合稳定图进行结果选取。目前稳态图中模态的选择多数是通过人工完成，这不仅增加使用者的工作量，不适用于在线分析情况，而且由于使用者在认识上存在着差异（易受虚假模态干扰），使得模态参数识别结果带有一定的主观性。因此为随机子空间算法引入一种模态自动选取方法是一项亟待解决的工作。

文献［3］提出借助模糊C均值算法对p_LSCF结果进行自动拾取，文献［4］提出一种改进的谱系聚类算法对LSCF结果进行自动选择，都取得了良好的效果。本文以基于协方差驱动的随机子空间算法进行参数估计，针对其计算结果中大量虚假模态影响结果拾取的问题，提出一种能够衡量模态可靠性的指标称之为模态相似指数，将其结合模态能量以剔除计算结果中由噪声、模态过估计等因素引起的虚假模态；以频率、阻尼比、模态振型、模态能量为聚类因子计算结果中各模态之间的相似性，采用谱系聚类法根据模态之间的相似性将计算结果分成若干类，提取元素个数大于一定值的类作为拾取结果。通过一个数值仿真以及实例分析验证本文方法可以实现系统物理模态地自动拾取。

1 随机子空间虚假模态剔除

1.1 基于协方差的随机子空间系统识别算法［1］

n自由度系统，其离散时间状态方程为：

其中：A∈R2n×2n：状态矩阵，B∈R2n×m：输入矩阵，C∈Rl×2n：输出矩阵，D∈Rl×m：直馈矩阵，m：输入个数，l：输出个数，Δt：采样间隔。

定义输出协方差矩阵Ri：

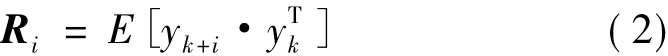
定义状态-输出协方差矩阵G：

可证明如下关系成立：

（1）构造Toeplitz矩阵

（2）矩阵块分解

将式（4）代入式（5）得到：

其中：Oi∈Ril×N为扩展可观测矩阵，Ti∈RN×li为扩展可控矩阵，N为系统阶次。

设W1和W2为两个可逆加权矩阵［2，5］，对加权 Toeplitz矩阵进行SVD分解，可以得到：

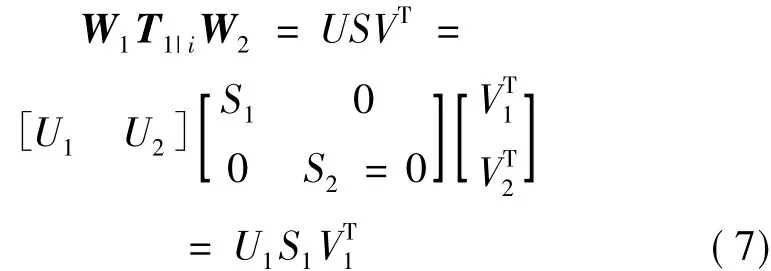
其中：U1∈Rli×N，S1∈RN×N，V1∈Rli×N。

结合式（6）和式（7）可得：

其中：（·）+表示矩阵的伪逆。

（3）模态参数的识别

由式（6）可以看出，C为矩阵Oi的前l行，G为Ti的后l列，用Matlab语言表达如下：

定义Oi的两个子矩阵T1和T2：

由式（10）可以看出：

对矩阵A进行特征值分解：

其中：Λ∈CN×N是一个对角矩阵，由离散时间系统的极点λi组成。系统参数可以由状态矩阵A、输出矩阵C得到［1］。

1.2 利用模态相似指数剔除虚假模态

定义矩阵B：

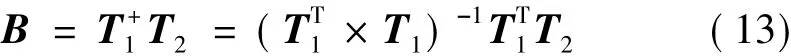
可以看出，对于系统特征值a（系统的真实极点）下式成立：

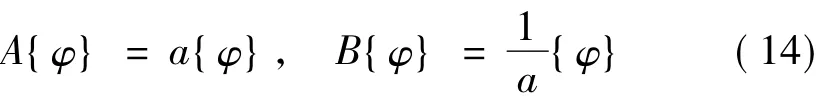
可以得到状态矩阵A新的估计方式：

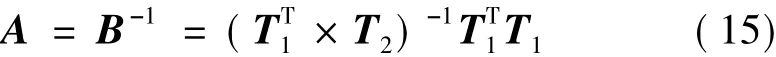
可以看出通过式（11）和式（15）得到的控制矩阵A具有相同的系统特征值，即两种方法所得结果中物理模态将会成对出现。而对于由噪声、阶次过估计等因素引起的虚假特征值则不具备以上性质，即两种方法所得结果中虚假模态不会成对出现。

以一数值仿真验证上述结论。一两自由度线性时不变系统在随机激励下振动，固有频率分别是13.78，18.38，阻尼比分别是 0.002 8、0.003 8，分别用式（11）和式（15）对响应信号进行极点估计（阶数假设为20）。两种算法结果的极点分布情况如图1所示，可以看出，两种方法结果对真实极点（物理模态）的估计是一致的（成对地出现），说明两种算法能有效地识别出了系统的物理模态；但是它们得到的虚假极点（虚假模态）则是不同的，不会成对出现。

图1 极点分布图（‘o’：式（11）结果，‘* ’：式（15）结果）Fig.1 The distribution of poles（‘o’：the results of Eqs.（11），‘* ’：the results of Eqs.（15））

定义模态相似系数：

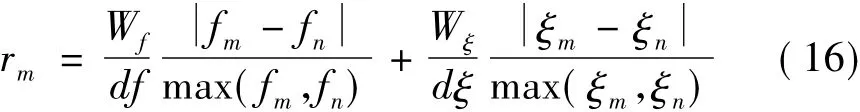
其中：fm、ξm为通过式（11）得到的频率和阻尼比，fn、ξn为通过式（15）得到的频率和阻尼比，df、dξ分别表示频率、阻尼比的容差，本文选取为 0.01、0.05，Wf、Wξ为频率、阻尼比在计算相似系数中的权值，本文取为0.7，0.3。

于是可以根据计算结果中的模态相似系数剔除虚假模态，基本步骤如下：

（1）在计算过程中分别用式（11）和式（15）计算系统的状态矩阵得到两组结果（频率f、阻尼比ξ）。

（2）对于通过式（11）计算得到的每个模态m都可以在通过式（15）计算的结果中找到频率最相近的模态n，并用式（16）计算相应相似指数rm。如果模态m，n之间的频率、阻尼比都在容差之内，那么rm将小于1，因此一般设定阈值为1。如果rm小于阈值，则可认为模态m与n属于同一模态，即模态m可以在式（15）计算的结果中找到相同的模态，认为其为真实模态，反之，则将其作为虚假模态予以剔除。

1.3 利用模态能量剔除虚假模态

由自然激励技术法（NExT）［6］可知，白噪声环境激励下结构响应的自相关函数和脉冲响应函数具有相似表达式：

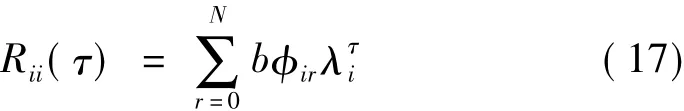
它由类似于系统各阶模态的自由响应信号叠加而成。由式（2）对输出协方差矩阵Ri的定义可得各输出信号能量之和如下式所示：

其中diag（·）表示用矩阵的主对角元素组成行向量，（·）T表示转置。

将式（4）代入式（18）可得：

将式（12）代入式（19）可得：

结合式（12）和式（20）可得各阶模态所贡献的能量为：

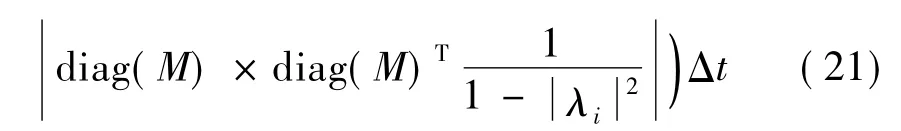
其中：M=Cψi（ψ-1）iG，ψi为矩阵 ψ 的第i列，（ψ-1）i为矩阵 ψ-1的第i行，（·）*表示共轭。

由输出信号的组成（如式（17）所示）可知，结构的输出能量应该是由各阶物理模态的能量之和，由噪声和模态过估计等因素带来的虚假模态对其贡献应该为零。因此，可以利用各阶模态能量贡献来判断其是否属于系统的物理模态。

2 模态参数自动拾取

基本步骤如图2所示，先利用随机子空间算法估计系统的模态参数并且根据本文提出的方法得到模态相似指数以及相应的模态能量，利用各模态的相似指数以及模态能量剔除部分虚假模态，对剩下的结果采用谱系聚类法进行聚类，根据类元素个数完成模态的自动拾取。

图2 自动识别算法流程图Fig.2 The flowchart of automatic identification algorithm

2.1 剔除部分虚假模态

为了减少计算结果中虚假模态对后续聚类分析的影响，在识别模态参数的过程中采用式（16）计算各模态相似指数，设定相似指数阈值剔除部分虚假模态，又由第1.3节分析可知，可以通过模态能量来判断虚假模态，对各假设模型阶数下计算出来的能量进行排序，将能量最大的前Np个模态保留用以进行后续分析，以进一步剔除计算结果中的虚假模态。

2.2 计算结果的聚类及物理模态的选取

传统的方法是从稳态图中手动选择极点，由于疏忽或者经验不足，选择不恰当的极点将会造成识别结果的不准确。由于模糊C均值算法存在着一些问题，如需要人为指定模态数、一些参数的最佳值难以设置等［3，7］，因此本文借助谱系聚类法（hierarchical clustering methods）对剩下的计算结果进行自动选择，将所有的计算结果组成一数据集，将距离在一定范围内的数据进行聚类，认为同一类中的数据属于同一模态，最后选择元素个数大于一定值的类作为识别结果。该方法在进行聚类之前需要建立距离矩阵，因此需要定义一个反映模态之间距离的统计量，以频率f、阻尼比ξ、模态振型ψ和模态能量P作为为聚类因子，定义模态i，j之间的距离dij如下：

其中：df、dξ、dψ、dp分别表示频率、阻尼比、模态振型、模态能量的容差，本文选取为 0.01、0.05、0.02、0.1；Wf、Wξ、Wψ、Wp表示频率、阻尼比、模态振型、模态能量在计算模态距离中的权重，它们之和为1，本文选取为0.25、0.25、0.25、0.25。

在距离矩阵建立完毕之后，便可以设定距离阈值对模态进行聚类。由式（22）对距离的定义可以看出，如果模态i，j之间的频率、阻尼比、模态振型、模态能量比值都在容差之内，那么dij将小于1，因此一般设定距离阈值为1。当聚类完成之后，统计每个聚类中包含的模态个数，认为聚类数目大于阈值Nm的聚类为有效聚类，提取离类中心最近的数据为识别结果。

3 数值仿真

以一悬臂梁模型作为仿真实验件，结构如图3所示，材料属性：梁长度l=1m，横截面积A=1×10-4m2，体密度D=7830 kg/m3，弹性模量E=2.068 ×1011，泊松比K=0.3。

图3 悬臂梁模型Fig.3 The model of a cantilever beam

对梁施加白噪声激励，同时在各测点处（x1、x2、x3、x4、x5）测试位移响应。采样频率为1 000 Hz，采样时间为10 s，给每个通道加10%的随机噪声。

利用基于协方差驱动的随机子空间算法对数据进行分析，图4是用传统方法得到的稳定图（其中‘s’表示稳定点，‘v’表示频率和振型稳定的点，‘d’表示频率和阻尼比稳定的点，‘f’表示频率稳定的点。），图5为利用模态相似指数及模态能量（Np=5）剔除虚假模态后的稳定图，可以看出剔除虚假模态后所得到的稳定图相比原始稳定图少了许多虚假模态干扰，有利于物理模态的拾取，接着利用谱系聚类法自动选定模态（Nm=20），表1是本文方法识别的结果与悬臂梁前5阶理论值之间的对比（频率、阻尼比以及对应振型之间的MAC值），可以看出本文提出方法所识别的结果与理论值误差很小（固有频率的误差在0.72%以内，阻尼比误差在6%以内，对应振型之间的MAC值为1）。数值仿真实验说明了本文提出的方法可以在不需要人为参与的情况下正确地识别出物理模态。

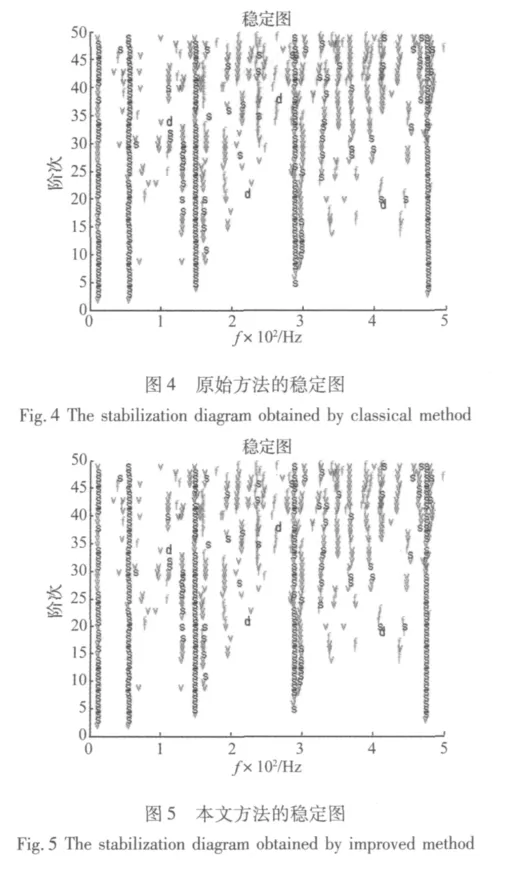
表1 识别结果与理论值的比较Tab.1 The compration between identified result and the theoretical value

4 实例分析

为了进一步验证本文方法的有效性，将该方法应用于重庆华福桥模态参数识别实验，桥梁在过往行人、车辆以及自然环境中的风流动等随机激励下振动，在桥梁竖向上共设置了11个测点，由加速度传感器采集，每个测点的数据记录长度为4 k，采样频率为200 Hz，图6为桥梁立面图。

图6 华福桥桥梁立面Fig.6 The bridge elevation of hua fu bridge

对采集到的信号采用随机子空间进行参数识别，首先根据模态相似指数与模态能量（Np=15）对计算结果进行虚假模态剔除，接着用本文提出的自动识别算法进行模态自动拾取（Nm=20），将结果与原始随机子空间方法识别方法结合稳定图人工选取的结果和特征系统实现算法（ERA）所得到的结果对比如表2所示。

结合图7（剔除虚假模态后的稳定图）及表2可以看出，稳定图中稳定性较好的数据已全部被选取，由于本文数据已经过多种方法分析，原始算法及ERA结果的选取有了一些参考，因此通过它们得到的结果是可靠的，从表2可知，本文算法的自动识别结果与其他两种算法的结果一致（ERA算法虽然没有得到第1阶和第5阶模态，但其他相应的模态结果与本文结果也是非常接近的），并且其大部分结果都最靠近三者相应结果的平均值，以上进一步说明了本文所提出方法得到的结果是可靠的。

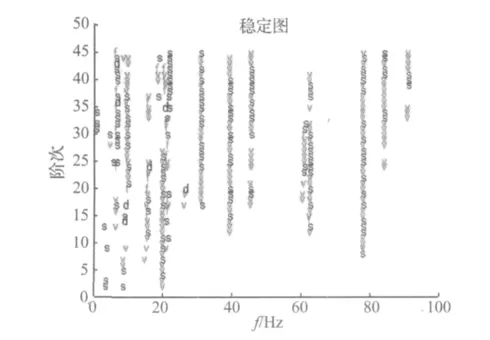
图7 本文方法的稳定图Fig.7 The stabilization diagram obtained by improved method

表2 华福桥识别结果对比Tab.2 Compration of the identification results of hua fu bridge

5 结论

（1）提出一种模态可靠性的衡量指标称之为模态相似指数，并结合各阶模态的能量有效地剔除计算结果中的虚假模态。

（2）引入谱系聚类法进行模态结果拾取，根据计算结果之间的相似性将计算结果分成若干类，提取类元素大于阈值的类作为拾取结果，实现物理模态地自动拾取，提高了识别效率，免除人为因素的干扰。

（3）通过数值仿真和实例分析验证本文方法的有效性。

［1］ Peeters B，Roeck G de.Reference-based stochastic subspace identification for output-only modal analysis［J］.Mechanical Systems and Signal Processing，1999，（13）：855-878.

［2］ Peter V O.Bart D M.Subspace identification for linear systems：theory-implementation-applications［M］.Dordrecht，the Netherlands：Kluwer Academic Publishers，1996.

［3］姜金辉，陈国平，张 方，等.模糊聚类法在试验模态参数识别分析中的应用［J］.南京航空航天大学学报，2009，（3）：344-347.

［4］ Verboven P，Cauberghe B，Parloo E，et al.User-assisting tools for a fast frequency-domain modal parameter estimation method［J］.Mechanical System and Signal Processing，2004，（18）：759-780.

［5］Hermans L，Van der Auweraer H.Modal testing and analysis of structures under operational conditions： industrial applications［J］.Mechanical Systems and Signal Processing.1999，13（2）：193-216.

［6］王 济，胡 晓.Matlab在振动信号处理中的应用［M］.北京：中国水利水电出版社，2006.

［7］高新波.模糊聚类分析及应用［M］.西安：西安电子科技大学出版社，2004.