改进溢出判断电路的设计与仿真研究

王 颖 ，王瑞春

（1.深圳信息职业技术学院 电子与信息学院，广东 深圳 518055；2.深圳信息职业技术学院 基础部，广东 深圳 518055）

溢出现象的判断是固定字长有符号加法运算中必须要进行的操作，传统溢出现象的判断要等到加法运算结果产生以后才能进行，本文电路设计能够在加法运算开始之前通过对操作数的判断而进行溢出预判，从而减少了整个加法/减法运算的时间。

溢出现象有可能出现在有符号数的加法或减法运算中，在进行固定字长的有符号数加法或减法运算时，如果出现以下四种情况：正数与正数相加得到负数、正数减负数得到负数、负数减正数得到正数、负数加负数得到正数，则认为有溢出现象产生。

1 传统溢出判断电路的设计[1]

传统溢出判断电路的设计是建立在加法或减法运算已经产生结果的基础上，如果用Overflag表示当前的运算方式，当Overflag取值为“1”时表示的是进行有符号数的加法或减法运算，当Overflag取值为“0”时表示的是进行无符号数的加法或减法运算。用Adder表示当前的运算方式是加法或者减法运算。当Adder取值为“1”时表示进行加法运算，当Adder取值为“0”时表示进行减法运算。用A[3]、B[3]和R[3]分别表示两个操作数和加减法运算结果的最高位即符号位。用Overflow表示溢出结果，如果Overflow取值为“1”则表示产生了溢出；如果Overflow取值为“0”则表示没有产生溢出。如果利用 Carry-Lookahead Adder[2]算法来产生 R[3]，则结合对溢出产生条件的分析，可以得到溢出判断电路图如图1所示。

2 具有预判功能的改进溢出判断电路的设计

具有预判功能的溢出判断电路设计的原理是将Carry-Lookahead Adder[2]的算法与传统溢出逻辑判断逻辑算法相结合。如果将可能产生溢出的四种运算都转换为加法运算，则在有可能产生溢出的四种运算情况下只要数值位向符号位产生进位或者符号位本身相加产生进位就可以判断有溢出产生。因此在电路实现上需要有两部分功能块，一部分是判断当前的运算是否为可能产生溢出的四种运算，将这部分功能块称为初步判断功能块；另一部分是判断数值位的最高位有无向符号位产生进位或符号位本身相加有无进位产生，将这部分功能块称为进位判断功能块。最后需要将两部分功能块结合在一起成为完整的溢出预判电路。

图1 传统溢出判断电路结构图

2.1 初步判断功能块的设计[1]

可能产生溢出的四种运算中，操作数的符号位即A[3]和 B[3]及加/减法控制信号Adder的取值与初步判断功能块的输出信号F的关系如表1所示。

由此表1可以得到F与A[3]、B[3]和 Adder之间的逻辑关系如下：

2.2 进位判断功能块[2]

在对溢出现象进行分析的过程中发现，可能产生溢出的四种情况的运算最后都可以转换为加法运算，具体分析如下：

正数与正数相加，原本就是加法运算，所以毋须进行转换。

正数减负数相当于正数与同负数有相同绝对取值的正数进行相加。即只要将被减数转换成与其本身有相同绝对取值的正数即可。

负数减正数相当于负数与同正数有相同绝对取值的负数进行相加。即只要将被减数转换成与其本身有相同绝对取值的负数即可。

负数加负数本身就是加法运算，毋须进行转换。

假设A为加法或减法运算中的第一个操作数（被加数或被减数），B为第二个操作数（加数或减数），由以上分析可以发现，A不需要做任何变换，而B要根据需要进行变换，变换后的数字用D进行表示。对B进行变换的算法为：首先判断条件“A[3]=0且 B[3]=1且 Adder=0”或“A[3]=1且 B[3]=0且 Adder=0”是否成立，如果条件成立，则D的值等于对B做减1运算后再取反的数值，否则D=B。

操作数B做了变换后，A与B的运算就转换成A与D的加法运算，运算结果用R表示。通过前面的分析可以发现在可能产生溢出的四种运算情况下（即：正数与正数相加、负数与负数相加、正数与负数相减、负数与正数相减），只要A与D的加法运算的结果中符号位的符号与操作数符号相反就标志着产生了溢出。用Ci+1表示第i位向第i+1位产生的进位，则C3=1或C4=1且C3和C4不能同时为1时标志着溢出的产生。

通过对Carry-Lookahead Adder[2-3]的分析可以发现进位的产生不必等到加法运算结束，即：

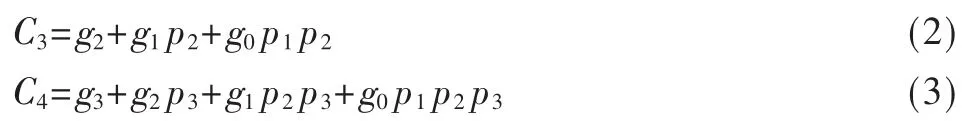
其中 gi=AiDi，pi=Ai⊕Di（i表示第 i位数据）。

进位判断电路如图2所示。

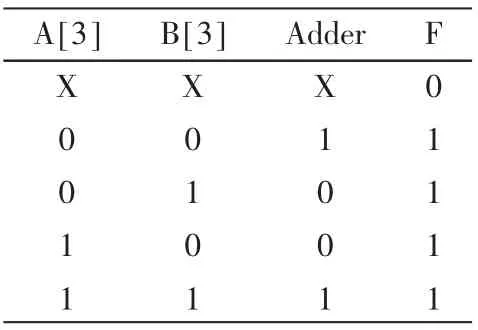
表1 初步判断功能块输入输出信号关系

2.3 完整的具有预判功能的溢出判断电路

在图2中，进位信号C[3]或C[4]当且仅当其中一个取值为1并且当前的运算为溢出可能出现的四种情况之一时，标志着产生了溢出。所以完整的溢出预判电路需要将进位判断电路与初步判断电路进行结合，结合后的溢出结果信号 Overflow与 F、C[3]、C[4]及 Overflag的逻辑表达式如下：

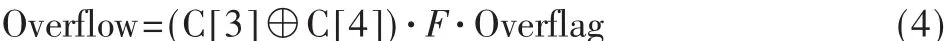
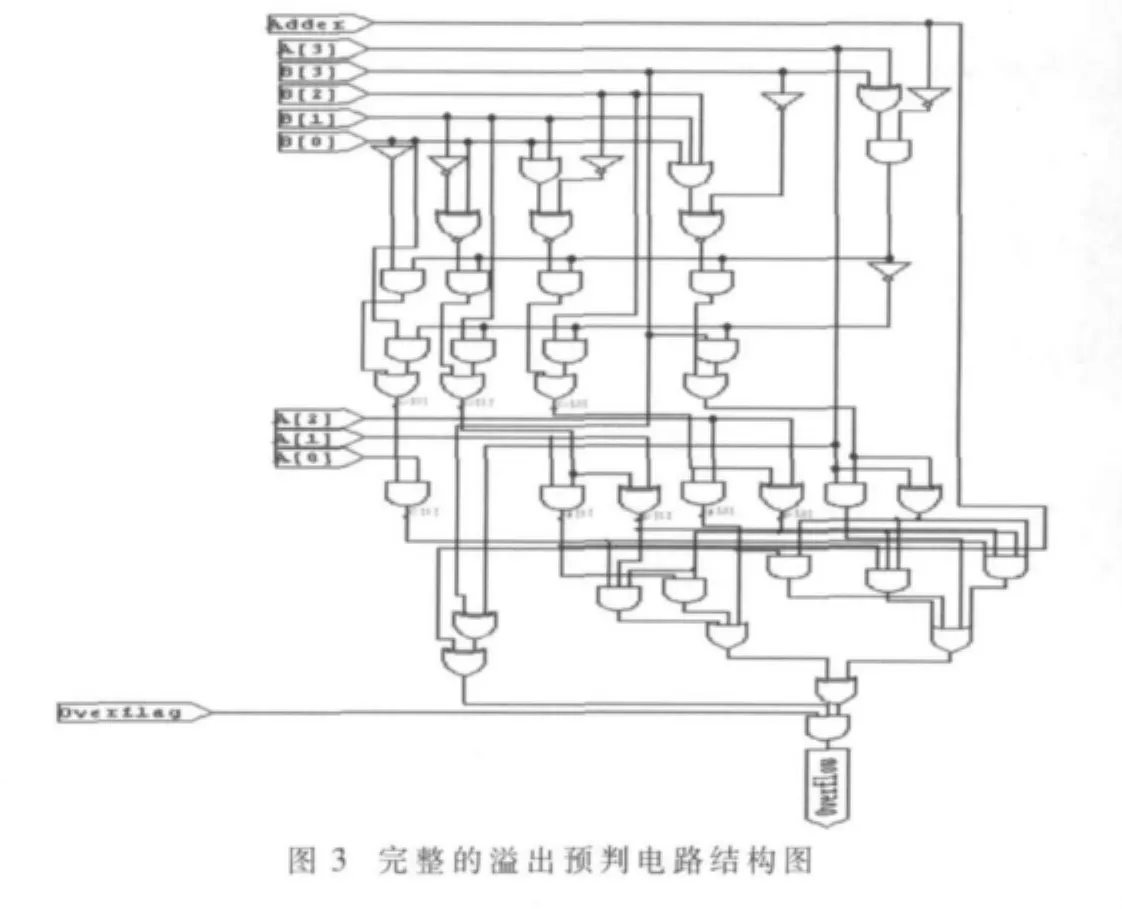
完整的电路图如图3所示。

通过比较图3与图1的电路结构发现，改进的溢出判断逻辑电路图在结构上要精简许多。

2.4 逻辑验证

电路的功能验证利用TSPICE实现，仿真得到的波形如图4所示。在仿真波形图中，从上至下信号名依次为Overflag，Adder，A[3]，A[2]，A[1]，A[0]，B[3]，B[2]，B[1]，B[0]和 Overflow。通过分析仿真波形图中输入的 A、B、Adder、Overflag共17组验证数据与输出信号 Overflow的关系可以证明该电路能够正确判断溢出的产生情况。

2.5 延时比较

Adder到Overflow的路径为溢出判断电路的关键路径，通过仿真工具TSPICE分别计算两种电路结构中关键路径的延时，在相同的仿真条件下，改进溢出判断电路中从Adder到Overflow的延时为11.697 ns，传统溢出判断电路中从Adder到Overflow的延时为12.232 ns。

本文在传统溢出判断电路的基础上，提出一种改进的电路结构，在这种改进结构中，不必等到加减法运算结果的产生就能预先判断有无溢出现象的发生。通过仿真发现，这种结构在能够实现所需的逻辑功能的基础上减少了电路规模，并减少了传输延迟。

[1]王颖.数字芯片溢出逻辑电路的设计与仿真研究[J].微计算机信息，2010，02（26）：160-163.

[2]OMONDI A R.Computer arithematic systems-algorithms,architecture and implementation[M].Prentice-Hall，1994.

[3]PARHAMI B.Computer arithmetic-algorithms and hardware designs[M].Oxford University Press，2000.

[4]刘杰，易茂祥.6加数并行加法器及扩展接口的研究[J].微电子学与计算机，2009，12（12）：27-30.