光滑有限元的声学研究：时域和频域分析

何智成，李光耀，成艾国，钟志华，周 泽

(1.湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082;2.新加坡国立大学 机械工程系工程科学高级计算中心，新加坡 117576)

光滑有限元的声学研究：时域和频域分析

何智成1，2，李光耀1，成艾国1，钟志华1，周 泽1

(1.湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082;2.新加坡国立大学 机械工程系工程科学高级计算中心，新加坡 117576)

在使用有限元进行声场的数值模拟中，存在着两个主要误差，一个是数值方法中常规的插值误差，另外一个是计算声学中所特有的耗散误差(dispersion error)，后者则是影响声学模拟仿真置信度的最重要因素。产生耗散误差的本质原因是由于有限元的数值模型刚度“偏硬”造成的。为了控制耗散误差，最重要的是使数值模型更好地反映真实模型。采用一种基于边光滑的有限元方法(ES－FEM)来对声场的时域和频域进行数值模拟研究。该方法只采用对复杂问题域适应性很强的三角形网格，通过引进基于边的广义梯度光滑技术，使得有限元系统得到适当的“软化”。时域和频域的算例表明了在使用同样网格的情况下，该方法在声学模拟中的精度比有限元模型高。

边光滑有限元;声学;时域;频域

随着人们对汽车乘员舱的声学品质要求越来越高，汽车的NVH性能研究已经成了当今的研究热点。一般来说，汽车的振动噪声分为低频噪声(1～200 Hz，主要为结构噪声)，中频噪声(200～500 Hz)以及高频噪声(＞200 Hz，主要为风噪)［1］。有限元仍然是现在分析结构噪声或者声场的主要方法，虽然在现有的CAE商业分析软件中，有限元能够分析各种各样的声学问题，但是由于有限元系统的刚度偏硬［2］，从而使得声波在有限元数值模型中传播的速度大于实际的声速，从而导致了声波的传播模拟时存在很大的误差。由于数值模型刚度的差别，在频域方面则主要体现在有限元模拟产生一个除了常规插值误差以外的耗散误差(dispersion error)，这个误差也是中高频声场计算的主要误差［3］。因此有限元在声波传播问题的模拟技术以及中高频声学问题的仿真技术都还不太成熟。

为了提高声学仿真模拟的精度，控制有限元的耗散误差，最根本的方法是适当软化有限元系统的整体刚度，从而使得有限元声学模型的刚度接近真实模型刚度。为了软化有限元系统的刚度，一方面可以通过增加有限元网格的剖分密度，另一方面也可以通过提高有限元插值的阶数［4－5］，使得有限元系统变软，从而在计算声场中得到令人满意的结果。有些学者通过其他新的方法来控制计算声场的耗散误差，如无网格方法［6］，间断有限元法［7］。但是这几种方法实现比较复杂，而且这几种方法都是通过增加计算时间来换取的比较好的精度。

为了在声学数值模拟中得到较好的精度，本文采用了一种新型的光滑有限元技术。它采用光滑的迦辽金弱形式［8－9］来离散问题域，通过引入的梯度光滑技术，使得有限元系统得到适当软化，从而较好的模拟声场。这种方法尤其能在三角形和四面体网格的计算中得到很好的精度，并且由于这两种网格对任意复杂的模型具有很好的适应性，所以这种方法能够很方便的计算任何复杂模型。另外在效率上，这种方法在力学模型中的计算效率比有限元和无网格都要高［10］。因此本文采用这种光滑的有限元来技术对声学的时域和频域进行研究，数值结果表明了这种新方法能够在声学模拟中得到很好的精度。

1 声学计算的数学模型

1.1 声学数值模拟的强形式

假定声波传播的介质是理想流体，无粘滞性，在任意形状的封闭声场域Ω，声场状况可以用关于 p的波动方程描述：

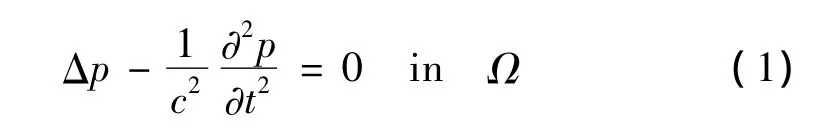
其中：Δ为Laplace算子，c为声波在介质中传播的速度，t为时间。在实际中，所计算的问题都是有边界的，其边界条件包含Dirichlet边界条件、Neumann、Robin边界，分别用ΓD、ΓN和ΓA表示，其边界条件的控制方程可以表示为：

其中：ρ为声音传播介质的密度，v为声学流体粒子的运动速度。

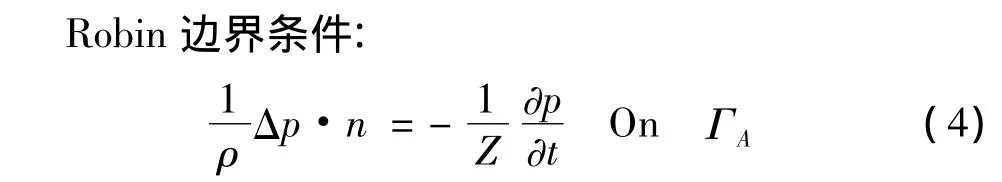
其中：Z为边界的阻抗，一般来说Z=1/An，An为边界的导纳。

在线性声学中，声压梯度与速度满足如下的欧拉方程：

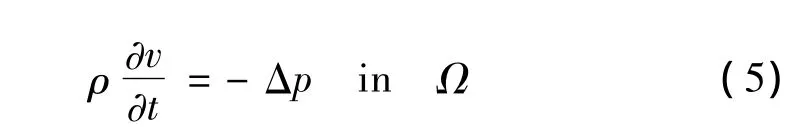
1.2 声学计算的弱形式

声场的弱形式可以通过光滑的迦辽金弱形式(Smoothed Galerkin weak form)对控制方程(1)进行离散得到，光滑的迦辽金弱形式离散化的详细过程可见文献［9］。声场的光滑迦辽金弱形式可以写为：

引入基于边的梯度光滑技术对协调梯度场进行修正，并在光滑域内进行高斯积分，形成并组装刚度矩阵，因此光滑有限元中的刚度矩阵不同于有限元的刚度矩阵，它是对于光滑域的积分，而不是对于单元的积分。

2 光滑有限元模型的建立

对于任意二维问题，首先用3节点的三角形网格(记为T3)对问题域进行离散，得到了域内的x个节点和N条边，如图1所示。则基于边k的光滑域Ωk(k=1，2，…，N)的构造过程为：如果边在问题域的内部，则围绕边k，用虚线分别联接其边的两个端点和相邻三角形网格的中心点，形成光滑有限元的基本单元即光滑域;如果三角形的边在问题域的边界上，则以全局边界封闭光滑域。图中n表示光滑域Ωk的边界外法线向量。该光滑域作为ES－FEM形成和组装刚度矩阵的基本单位，类似于有限元中的单元。ES－FEM的刚度矩阵是对这些光滑域Ωk进行数值积分来形成和组装刚度矩阵。通过类似的方法，光滑域的构造可以拓展到三维的四面体网格中，在三维光滑域构造中，光滑域模型的构造基于四面体的每个面：通过连接相邻四面体的中心及四面体的面的三个顶点，从而形成基于面光滑的光滑有限元的基本单元，具体细节可以参考文献［9］。

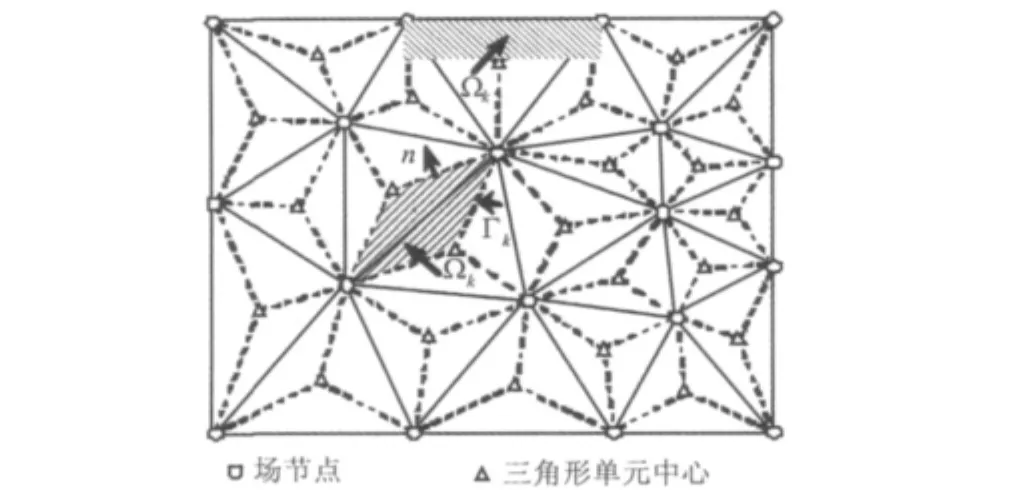
图1 基于三角形网格的二维积分光滑域Fig.1 The smoothing domain based on the background triangular mesh

在声学中，采用广义梯度光滑技术对声场基本变量的梯度即速度(式(5))实施光滑操作，则光滑域Ωk的刚度矩阵可以写为［9］：

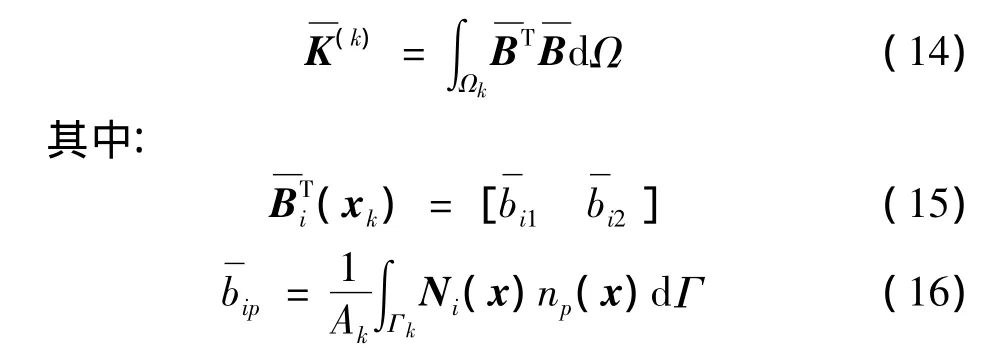
由式(15)、式(16)可以看出，通过广义梯度光滑技术，巧妙地将任意复杂的域内积分转换为简单的边界积分。对二维问题，则把面积积分转换为线积分。因此，与传统的有限元构造的梯度场相比，广义光滑梯度公式无需求解其形函数的导数，因而降低了对形函数连续可导的要求。

3 声学模拟的时域和频域模型

3.1 时域分析

在时域分析中，有许多的方法来模拟波的传播问题，像Newmark方法，Crank－Nicholson方法。本文采用Newmark方法，即在t～t+Δt的时间区域内，Newmark积分方法采用如下假设［11］：

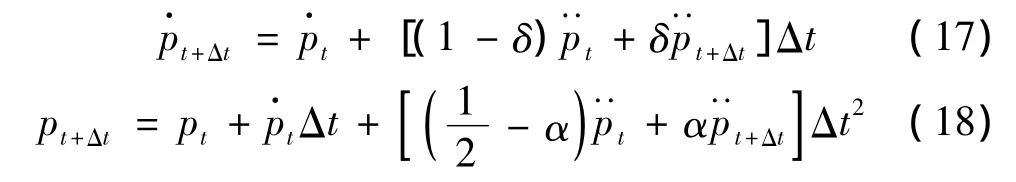
其中：α和δ是按积分精度和稳定性要求决定的参数，在这里α=0.25，δ=0.5，Newmark方法中的时间t+Δt的声压是通过满足时间t+Δt的控制方程所得到的，所以有：

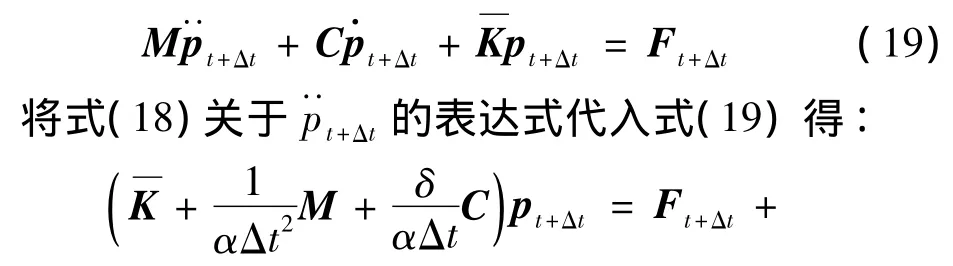
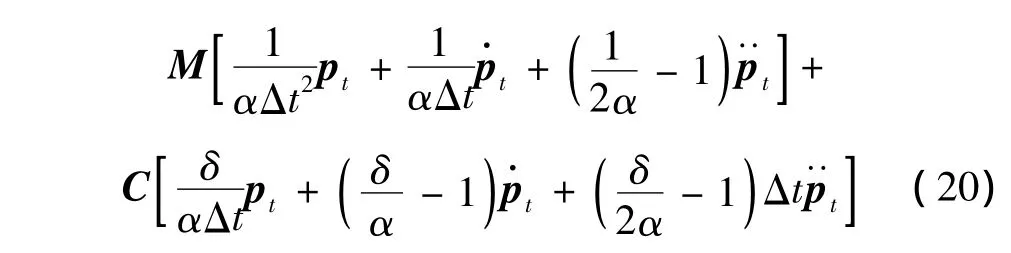
通过式(20)可以求解t+Δt时刻的声压，然后通过式(17)和(18)可以得到声压梯度(速度)。

3.2 频域分析

在频域中，声压及速度都可以表达成谐波的形式，因此p和v具有如下的表达式：

其中：Vn为边界上的法向速度，对于频率响应分析，在给定问题域及边界条件的情况下，都可以通过式(22)求出声场某点的频率响应。

在刚性边界条件下，自由模态的计算可以写成如下的表达式：

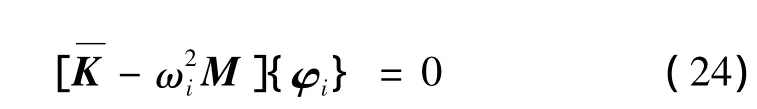
其中：ωi为模态特征值，φi为模态特征向量。

4 数值算例

4.1 时域模型算例——声波的传播

波的传播为例［13］，如图(2)所示，在管的左端作用是Dirichlet边界条件p=0，在管的右端作用v=H(t)阶跃速度边界条件，H(t)是Heaviside函数，即在小于或者等于零时，H(t)=0;在大于零时，H(t)=1。其他边界都为刚性壁条件。为了便于计算，取c=1，介质的密度为1.225 kg/m3。该模型被离散成的三角形网格的平均尺寸大小为0.05 m，具有207个节点和324个单元。该模型分别采用FEM和ES－FEM来计算声波的传播过程。取管子右端点A和中间点B(如图2所示)的响应来比较两种算法的准确度。

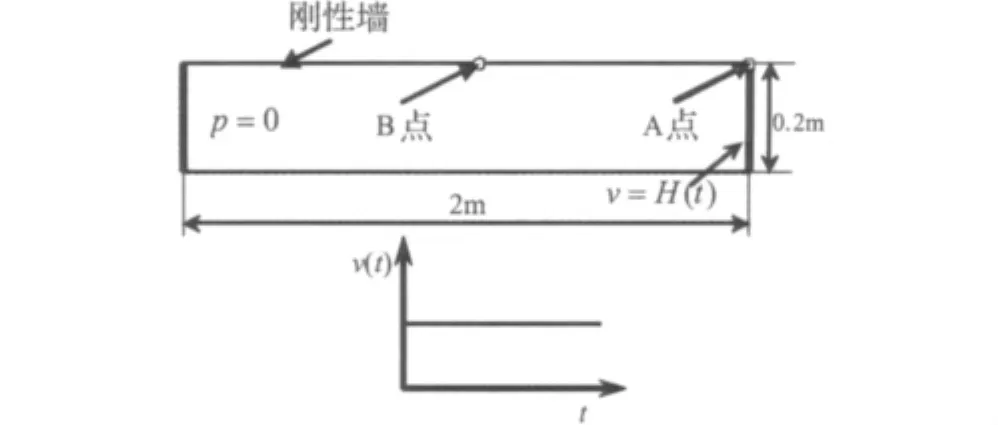
图2 含Heaviside类型激励的长方形管道Fig.2 Rectangle tube under Heaviside－type excitation

图(3)、图(4)分别为图(2)中所示两点的计算结果曲线。图中都对有限元(FEM)，光滑有限元(ES－FEM)及理论解(Exact)的计算结果都进行了标明。通过比较发现：在节点和网格数相同的情况下，ES－FEM得到的声压结果比有限元的结果要精确得多，如图3(a)，图4(a)。在图3(b)、图4(b)中，随着时间的变化，有限元计算结果的误差不断得到积累，越来越偏离理论解，而光滑有限元在整个时间历程上一直和理论解都很吻合。为了进一步说明方法的优越性，本算例也采用有限元方法计算了两种更密节点数的模型，计算模型和结果分别表示为FEM*(节点个数为729，单元个数为1 280)和FEM＊＊(节点个数为2 737，单元个数为5 120)。由图中可以看出，随着网格的加密，有限元的声压和速度计算结果越来越精确，从而越来越接近理论解;通过与基于粗网格(207个节点和324个单元)计算的光滑有限元结果比较，发现采用ES－FEM计算的结果好于FEM*的结果，甚至和FEM＊＊的计算结果差不多，误差在整个时间历程上一直都很接近理论解。由此可见ES－FEM在计算时域问题具有明显的优势。这主要是由于基于边光滑的有限元系统，能够适当地软化过刚的有限元系统，从而更好地模拟真实的模型，提供比较精确的梯度解，因此与相同网格下的有限元计算结果相比较，光滑有限元得到的解比有限元的计算结果要精确得多。

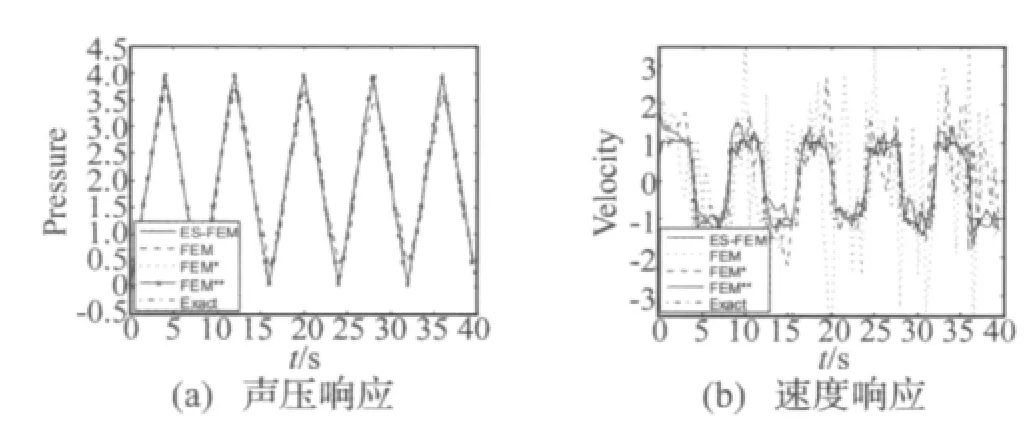
图3 A点响应Fig.3 The response of point A

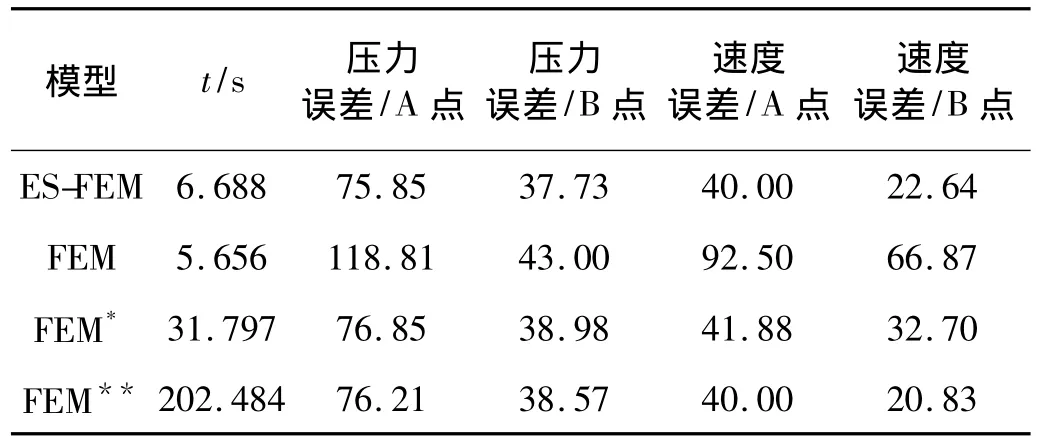
表1 计算成本和计算误差的比较Tab.1 The comparison of the computational cost and accuracy

为了进一步比较ES－FEM和FEM的计算成本，本文比较了在相同网格的前提下，光滑有限元和有限元的计算时间，另外同时也计算出了A，B点声压和速度在0～40 s整个时域内的误差，如表1所示。从表中可以看出，在相同的模型基础上，ES－FEM的计算时间比FEM的计算时间稍长，但是ES－FEM得到的声压及速度结果比FEM的结果要精确得多。表1同时也列出了有限元采用两种较密网格模型的计算时间及计算误差。由表中可以看到，随着有限元网格密度的加大，计算时间越长，并且计算精度越高。但是相对于光滑有限元而言，FEM得到相同精度所消耗的时间远远要大于ES－FEM消耗的时间。由此可见，光滑有限元的相对计算成本(同等时间获得的精度)比有限元小。

4.2 频域模型算例

一般来说，消声器的内部声场比较复杂，平面波理论无法准确地预测其消声特性。为了计算消声器的消声性能，本文通过建立消声器内部声场的二维数值模型，如图5所示，并且对进出口及壁面的边界条件进行合理的处理，来研究了消声器的声学模态和传递损失(Transmission Loss，TL)。介质为空气，密度为 ρ=1.225 kg/m2，声速为c=340 m/s。该消声器离散成294节点494个单元，分别采用有限元及光滑有限元对其进行计算。由于此消声器没有理论解，理论证明［14－15］可以采用很密的网格，通过有限元求解得到问题的参考解。这里用来计算参考解的网格模型具有24 627个节点，48 273个四边形单元。

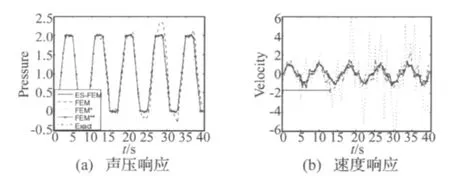
图4 B点响应Fig.4 The response of point B

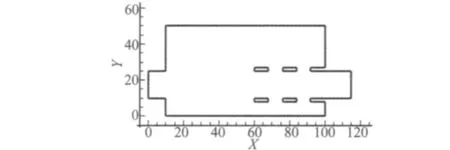
图5 消声器的二维图Fig.5 The illustration of the two－dimensional muffler

假如消声器的边界及进出口为刚性壁面，则消声器的声学模态可以通过有限元或者光滑的有限元求出。表2列出了有限元和光滑有限元求得的消声器的前十阶声学模态，采用有限元计算的参考解也列在表2中。通过对消声器模态的计算，发现有限元计算的模态特征值要比参考解要大，反映了有限元系统刚度偏硬的特性，而光滑有限元计算的模态特征值比有限元的结果小，反映了光滑有限元系统比有限元系统偏软。数据结果也表明了有限元的误差是光滑有限元误差的3，4倍左右，说明了光滑有限元系统相对有限元系统来说得到了适当的软化，更适合求解声学问题。

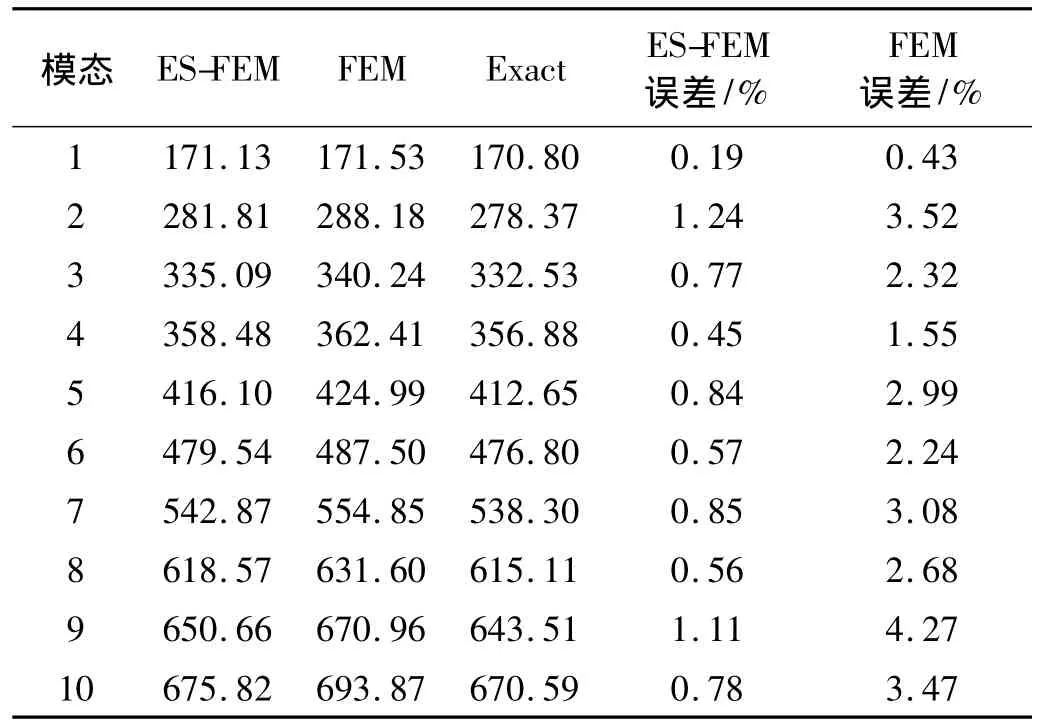
表2 消声器的声模态Tab.2 The eigenfrequencies of muffler

在计算消声器传递损失时，设置的边界条件要满足标准的边界条件定义，即在消声器的左边加一个单位的速度边界条件，即vn=1 m/s。在消声器的右边加完全吸声边界条件，即An=1/(ρc)。对于进出口面积相同的消声器的传递损失可以由以下的方式计算［11］：

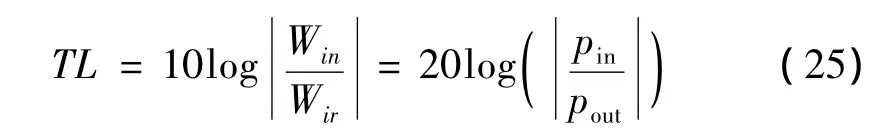
图6中为同种网格模型情况下，有限元和光滑有限元计算的消声器的传递损失曲线。为了便于比较，图6也提供了有限元采用两种不同网格模型的结算结果，分别表示 FEM*(节点个数为685，单元个数为1 222)和 FEM＊＊(节点个数为 1 519，单元个数为2 810)。另外在声学数值计算中，采用非常精细的网格可以得到与真实值相差很小的参考解，这里采用有限元计算参考解的模型含有24 627个节点，48 273个四边形单元。通过比较，可以看出，在低频段，有限元，光滑的有限元模型和参考解差不多，都十分接近参考解，但是随着频率的升高，ES－FEM的结果比FEM的结果更接近参考解，甚至达到了和FEM＊＊同等的精度。通过该算例，说明在相同的离散模型中，光滑有限元不论在低频或高频，数值结果都比有限元好。

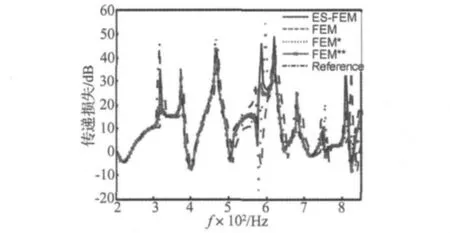
图6 ES－FEM和FEM计算的消声器的传递损失Fig.6 The transmission loss of the muffler using the present ES－FEM and FEM

5 结论

本文对基于边光滑的有限元在声学的时域和频域进行了研究，并且通过数值算例对该方法进行了验证，得到了如下的结论：

(1)该方法采用三角形单元，对任何复杂的问题具有很好的适应性，所以该方法适用于任何复杂的模型。

(2)该方法引入了梯度光滑的理论，能够适当软化过刚的有限元系统，从而得到比较精确的梯度场，因此比有限元更适合计算声波的时域问题。

(3)该方法计算的模态特征值要小于有限元得到的值，并且更接近参考解的值，因此该方法的数值模型系统刚度比有限元的软，因而在频域问题中，该方法比有限元具有更好的精度。

［1］庞 剑，谌 刚，何 华.汽车噪音与振动——理论与应用［M］.北京：北京理工大学出版社，2006.

［2］Liu G R.Meshfree methods：Moving beyond the finite element method［M］.USA：CRC Press，2009.

［3］Deraemaeker A，Babuska I，Bouillard Ph.Dispersion and pollution of the FEM solution for the helmholtz equation in one，two and three dimension［J］.Int.J.Numer.Meth.Engrg，1999，46：471－499.

［4］Petersen S，Dreyer D，Estorff O V.Assessment of finite and spectralelementshape functions or efficient iterative simulations of interior acoustics［J］.Comput.Methods Appl.Mech.Engrg，2006，195：6463－6478.

［5］Biermann J，Estorff O V，Petersen S，et al.Higher order finite and infinite elements for the solution of Helmholtz problems［J］.Comput.Methods Appl.Mech.Engrg，2009，198：1171－1188.

［6］ Bouillard Ph，Suleau S.Element－free Garlekin solutions for Helmholtz problems：formulation and numerical assessment of the pollution effect［J］.Comput.Methods Appl.Mech.Engrg.，1998，162：317－335.

［7］Alvarez G B，Loula A F D，Carmo E G D D，et al.A discontinuous finite element formulation for Helmholtz eqation［J］.Comput.Methods Appl.Mech.Engrg，2006，195：4018－4035.

［8］Liu G R.A weakened weak(W2)form for a unified formulation of compatible and incompatible methods，part I：theory and part II：applications to solid mechanics problems［J］.Int.J.Numer.Meth.Engrg，2010，81：1093 －1126.

［9］ He Z C，Liu G R，Zhong Z H，et al.An edge－based smoothed finite element method(ES－FEM)for analyzing three－dimensional acoustic problems［J］.Comput Methods Appl Mech Eng，2009，199：20－33.

［10］ Chen L，Nguyen H X，Nguyen T T，et al.Assessment of smoothed point interpolation methods for elastic mechanics［J］.Commun.Numer.Meth.Engng，2009，DOI：10.1002/cnm，1251.

［11］ Zienkiewicz O C，Taylor R L.The finite element method［M］.Butterworth－Heinemann：Oxford，2000.

［12］ Munjal M L.Acoustics of ducts and mufflers with application to exhaust and ventilation system design［M］.New York：Wiley，1987.

［13］ Wu T W.Boundary element in acoustics：fundamentals and computer codes［M］.Southampton：WIT Press，2000.

［14］ Ihlenburg F.Finite element analysis of acoustic scattering［M］.Springer Press，1998.

［15］ Ihlenburg F，Babuska I.Finite element solution of the Helmholtz equation with high wave－number part I：the hversion of the FEM［J］.Comput.Math.Appl，1995，30(9)：9－37.

Acoustic analysis using edge-based smoothed finite element method：time and frequency domain analysis

HE Zhi－cheng1，2，LI Guang－yao1，CHENG Ai－guo1，ZHONG Zhi－hua1，ZHOU Ze1
(1.State Key Lab.of Advanced Technology for Vehicle Body Design＆ Manufacture，Hunan University，Changsha 410082，China;2.Centre for Advanced Computations in Engineering Science(ACES)，Department of Mechanical Engineering，National University of Singapore，117576 Singapore)

The standard finite element method(FEM)encounters two kinds of errors in the computational acoustic problems：the conventional interpolation error and the dispersion error，the later of which plays an important role in the computational acoustics.The dispersion error is rooted at the"overly－stiff"property of the FEM.In order to control the dispersion error，the most effective measure is to make the numerical model reflect the exact model.An edge－based smoothed finite element method(ES－FEM)was adopted for acoustic problems both in frequency domain and time domain.By using only triangular mesh which is very adaptive for any complicated domain and introducing gradient smoothing operation performed over each edge－based smoothed domain，the present method can reduce the stiffness and provide proper“softness”to the model.The results demonstrate that the ES－FEM can provide more accurate solution both in time and frequency domain compared with the linear FEM using the same meshes.

edge－based smoothed element method(ES－FEM);acoustics;time domain;frequency domain

O42

A

教育部博士学术新人奖项目资助;教育部长江学者与创新团队发展计划(531105050037)

2011－04－26 修改稿收到日期：2011－08－23

何智成 男，博士生，1983年生

成艾国 男，教授，1972年生