基于DNA遗传算法的气动驱动柔性梁振动控制

邱志成，王 斌，石明礼，谢卓伟

(华南理工大学 机械与汽车工程学院，广州 510641)

基于DNA遗传算法的气动驱动柔性梁振动控制

邱志成，王 斌，石明礼，谢卓伟

(华南理工大学 机械与汽车工程学院，广州 510641)

采用气动脉冲码调制(Pulse Code Modulation，PCM)方式，给出一种基于有杆气缸驱动进行压电柔性梁振动控制系统。考虑到系统的复杂性，采用DNA－GA进行参数自适应整定控制。首先，介绍气动系统和控制回路;利用系统模型进行了能控性和基于性能指标函数控制算法的稳定性分析。其次，阐述了DNA－GA进行控制参数优化的原理和方法，进行了数学仿真研究。最后，建立了试验装置，进行同时气动定位和振动控制试验研究。理论分析、仿真和试验研究结果表明，采用DNA－GA参数自适应整定控制算法可改善控制系统动态性能，有效抑制柔性梁的大幅值低频模态振动。

气动驱动;压电柔性梁;振动控制;DNA－GA

柔性机械臂质量轻、功耗低，因此在工业场合和空间机器人中得到应用，但引起的振动问题需要控制。柔性机械臂的振动控制算法主要有模型参考自适应控制、自校正控制、前馈控制、基于观测器控制和常规PID控制等［1－2］。

气动系统具有高速、高效、工作可靠等优点。采用开关阀进行气动控制主要有脉宽调制 (Pulse Width Modulation，PWM)控制和脉冲码调制［3－4］(Pulse Code Modulation，PCM)控制两种方式。其中PCM方式采用一组开关阀串联的节流阀组成，PCM方式适合计算机数字I/O控制，操作简单。

常规PID控制控制参数对闭环控制系统的稳定性和性能有较大影响，现有多种方法调节。调节参数方法有：采用模糊控制算法整定参数［5］，采用遗传算法整定参数［6］;Kim 等［7］和 Huang 等［8］采用 DNA－GA 的方法整定参数，并进行了数学仿真研究。DNA－GA的整体结果与常规遗传算法相类似，但其采用的编码方法不同，且在这种编码方法的基础上进行遗传操作得到问题的解，故DNA－GA算法的收敛性同样能得到保证。

本文采用气缸驱动控制柔性机械臂低阶模态振动方案，气动回路上采用PCM出口节流控制方式。文献［9］对实验系统进行了初步研究，完成了系统建模和PD控制实验。本文与文献［9］相比，对实验系统的参数设定进行了调整，并采用信号滤波技术，目的是对小幅值高频颤振进行有效处理。本文采用DNA－GA进行PD参数在线优化自适应整定。结合系统模型进行了稳定性分析和数学仿真研究。最后，在建立的基于气动驱动的移动柔性梁实验平台上，进行了柔性梁的气动定位和振动抑制试验研究，并对常规PD控制和PD参数自适应整定实验进行了分析和比较。

1 系统描述

气动驱动柔性梁系统示意图如图1所示。柔性梁一端固定在气缸杆驱动沿导轨移动的滑块上。柔性梁表面粘贴一片压电陶瓷片PZT作为传感器测量振动。滑块的位移由位移传感器测量。

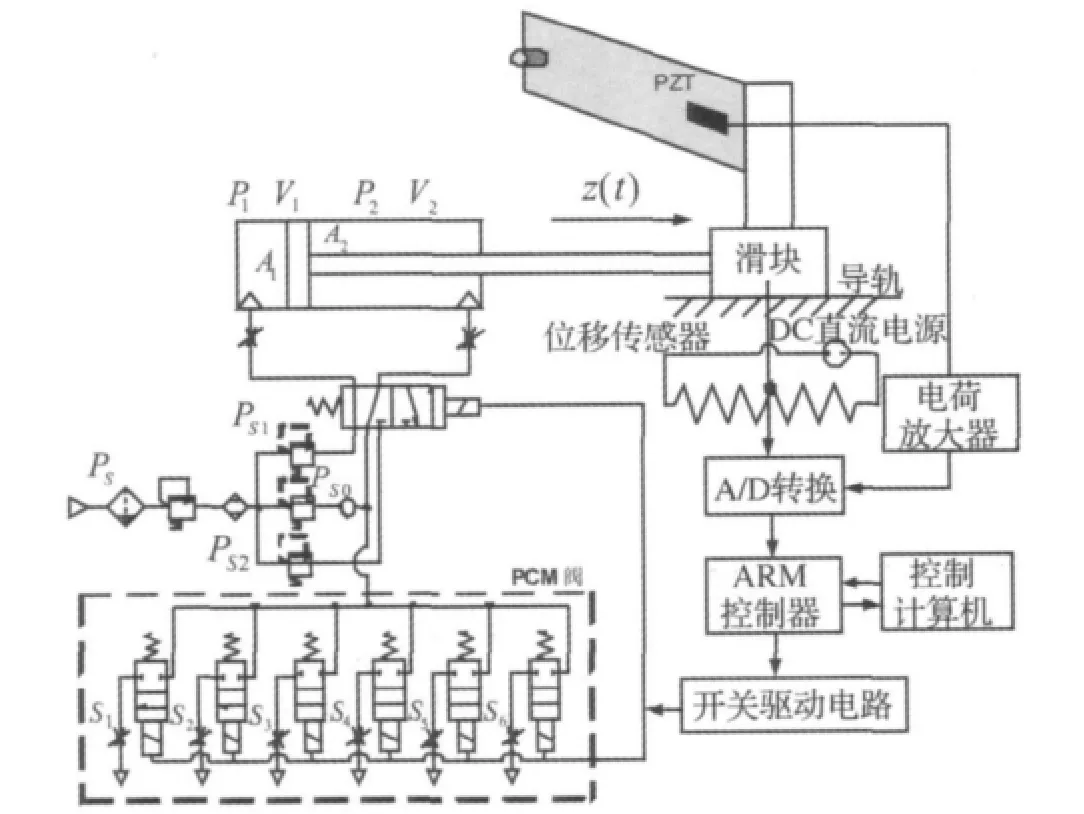
图1 气动控制系统Fig.1 Pneumatic control system

气动回路上，气源经过气动三联件后，分成三路并分别连接气动减压阀，其中两路连接两位五通阀驱动气缸左右运动的气源，一路串联单向阀后作为背压，与两位五通阀和PCM阀连接。当控制两位五通阀在左位或者右位时，分别控制气缸活塞向右或者向左运动。气缸运动的控制采用排气腔联通背压气源的PCM调节方式。气体排气流量大小通过PCM阀调节，即六个并联的开关阀分别串联节流阀，六个节流阀的开口面积为S1：S2：S3：S4：S5：S6=20：21：22：23：24：25，这样就可以得到64种组合面积的排气流量。

在控制回路上，压电片传感器检测柔性梁的振动经电荷放大器后，进行A/D转换，进入ARM处理器;气缸滑块位移由位移传感器检测，经过A/D转换后进入ARM处理器。ARM处理器将采样信号通过UART串口发送至上位控制计算机，运行复杂智能控制算法后，将控制信号传送给ARM处理器，再由ARM处理器将控制开关信号输出到开关驱动放大电路，控制一个二位五通阀的换向和六个PCM阀的开关动作，从而控制气缸活塞的运动。这里，PCM值的正负分别对应控制两位五通阀在左位或右位。

这样，就通过控制PCM阀同时实现了滑块的定位和柔性梁振动控制。具体的主从式控制方式如图2所示，系统控制的采样周期是在控制计算机设定的。

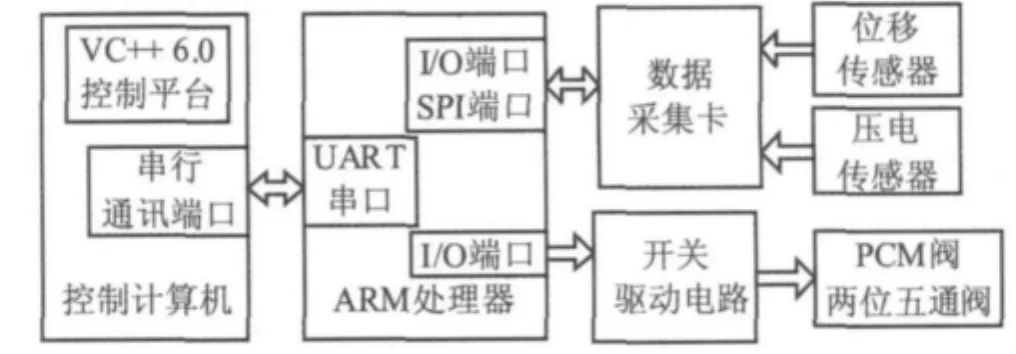
图2 主从控制系统Fig.2 Master/slave control system

2 系统模型

设t时刻滑块的位移为z(t)，柔性梁上距离根部x处点P的弯曲位移为w(x，t)，则P点的总位移为：

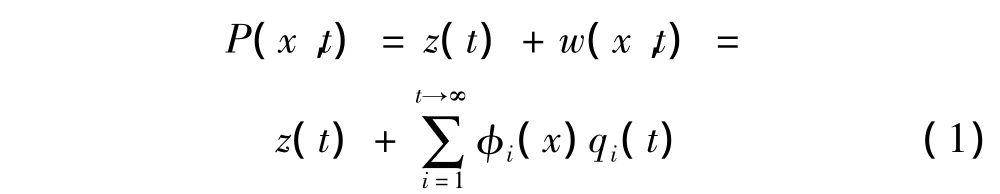
式中：φi(x)和qi(t)分别为柔性梁的第i阶模态函数和广义坐标。

根据文献［9］，有杆气缸驱动柔性梁系统活塞正向运动时系统的动态方程［9］：

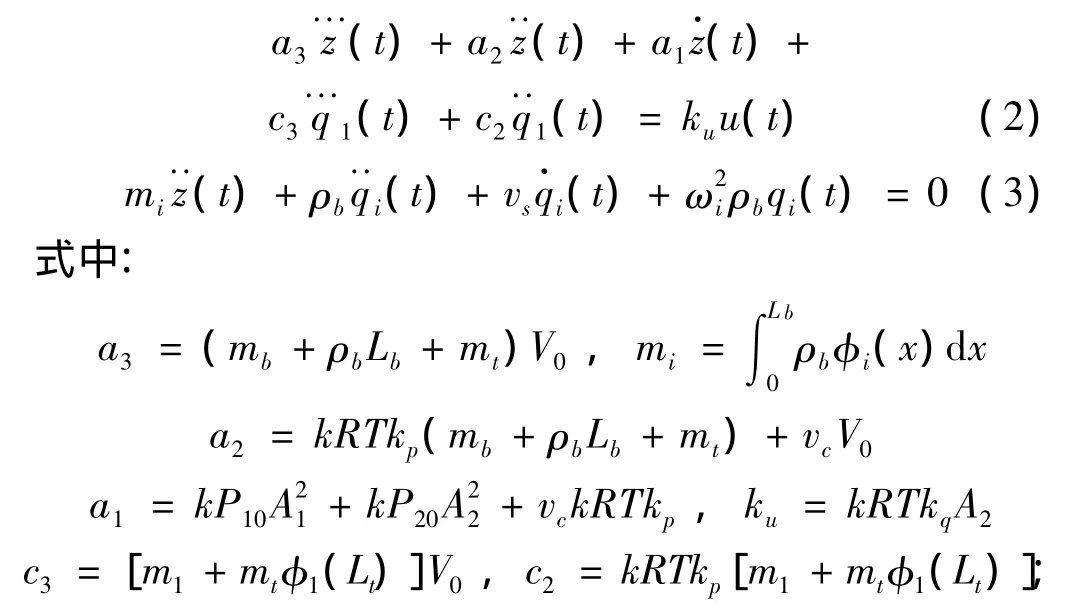
vc和vs分别为气缸运动粘性阻尼系数和柔性梁结构阻尼系数，k为空气绝热指数，R为气体常数，T为气体温度，kp和kq分别为气体流量压力增益和流量增益。加速度传感器质量为mt，距离柔性梁固定端为Lt。mb为滑块的质量，ρb为柔性梁线密度。Lb为柔性梁长度。A1和A2分别为气缸无杆腔和有杆腔活塞面积。

压电片传感器检测的电荷信号经过电荷放大器后，输出电压信号Vs：

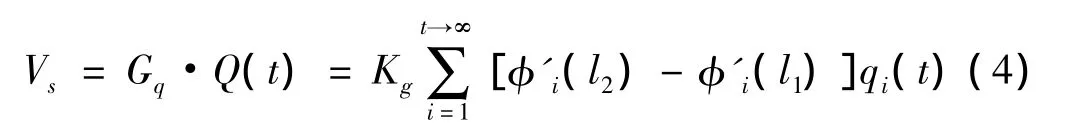
因为仅考虑柔性梁的一阶模态频率时，将系统的动力学方程表达为标准的状态空间形式：

3 控制算法及仿真

3.1 控制算法及稳定性分析

采用位移和压电片传感器信号反馈，同时控制滑块定位和柔性机械臂的振动的组合控制算法为：

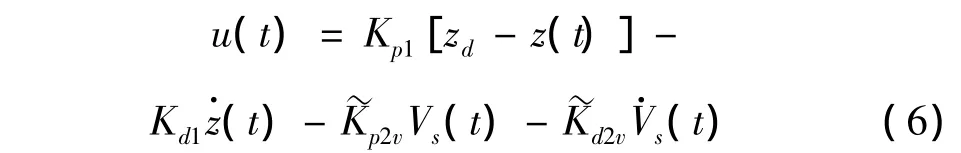
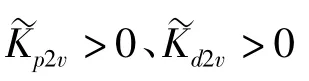
控制量u(t)的绝对值就对应PCM控制的数值，用来驱动控制PCM阀的开启和关闭。u(t)的正负就对应两位五通阀的开启和关闭，分别控制气缸活塞向左和向右运动。

在进行控制参数优化时采用目标函数为：

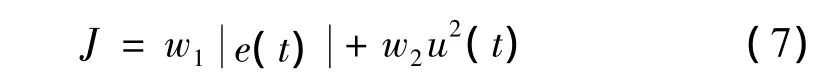
式中：e(t)为柔性梁振动的误差，u(t)为控制的输出量，w1和w2分别为系统误差和控制输出量的权值。

系统的能控性矩阵为：

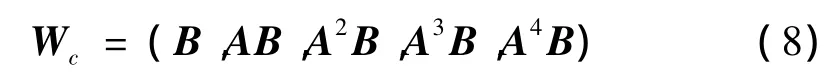
将系统矩阵A和控制矩阵B代入式(8)，可知能控性矩阵Wc满秩，因此该系统是可控的。

式(6)的控制u(t)还可以表达为：

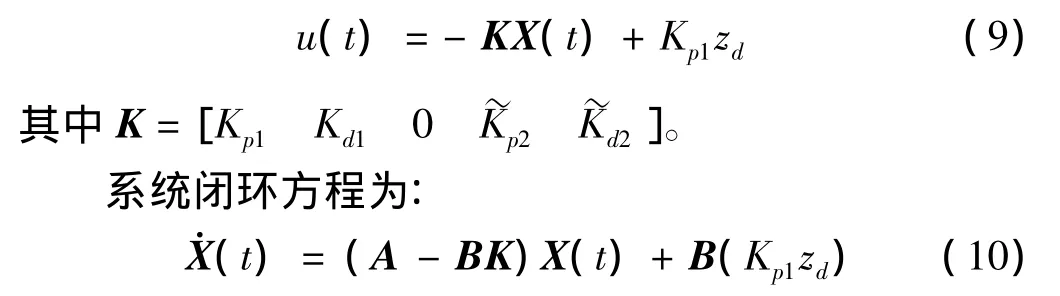
对闭环系统矩阵(A－BK)进行初等行变换，可得下三角形矩阵表达形式N：

闭环状态矩阵(A－BK)有五个特征根，且 Kp1、Kd1在设定的范围内，能保证 n11、n22和 n33的值为负且不为零，这样所有的特征根均具有负实部，矩阵(A － BK)是可逆的。并且，当 t→∞ 时，e(A－BK)t→0。

求解式(10)可得系统的状态为：

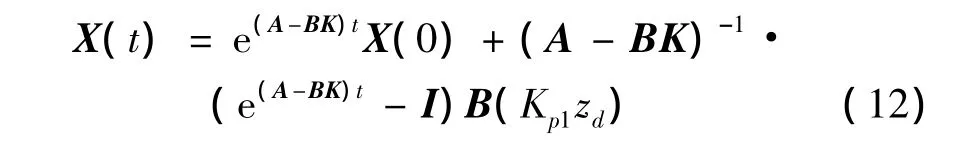
式中：X(0)为系统的初始状态，I为单位阵，e是自然对数的底数。

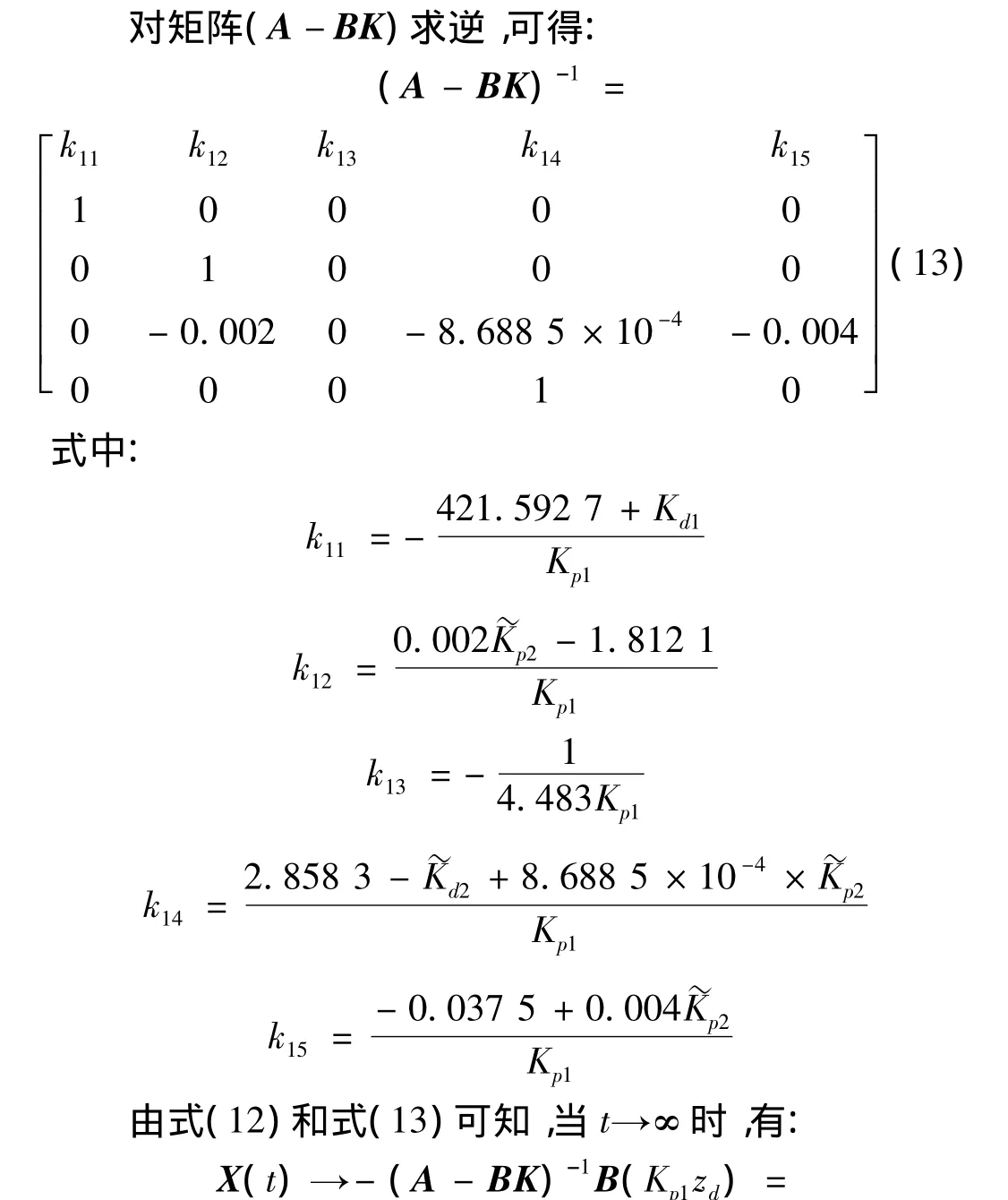
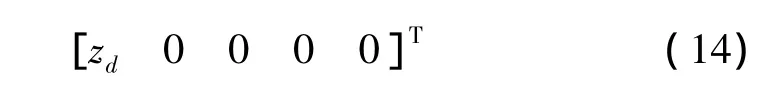
可知，采用的控制算法最终可以保证滑块位置趋向于目标位置zd，并且控制柔性机械臂的振动趋向于零。故而能实现抑制柔性梁的低频模态振动，并同时实现气动定位。

3.2 基于DNA-GA的控制参数优化

DNA－GA编码方式与遗传算法的二进制编码和十进制浮点数编码方式相比较，更适合复杂知识的表达，且比较灵活，具有编码的丰富性及译码的多样性，便于引入基因级操作。DNA－GA遗传操作如倒位、分离、交叉和变异等，大大地丰富进化手段。DNA染色体长度的可变性，使插入和删除碱基序列的操作更易实现，适合于复杂问题的优化［5－6］。

DNA－GA的结构流程图如图3所示。基于文献［7］和文献［10］，这里DNA－GA的具体实施步骤如下：

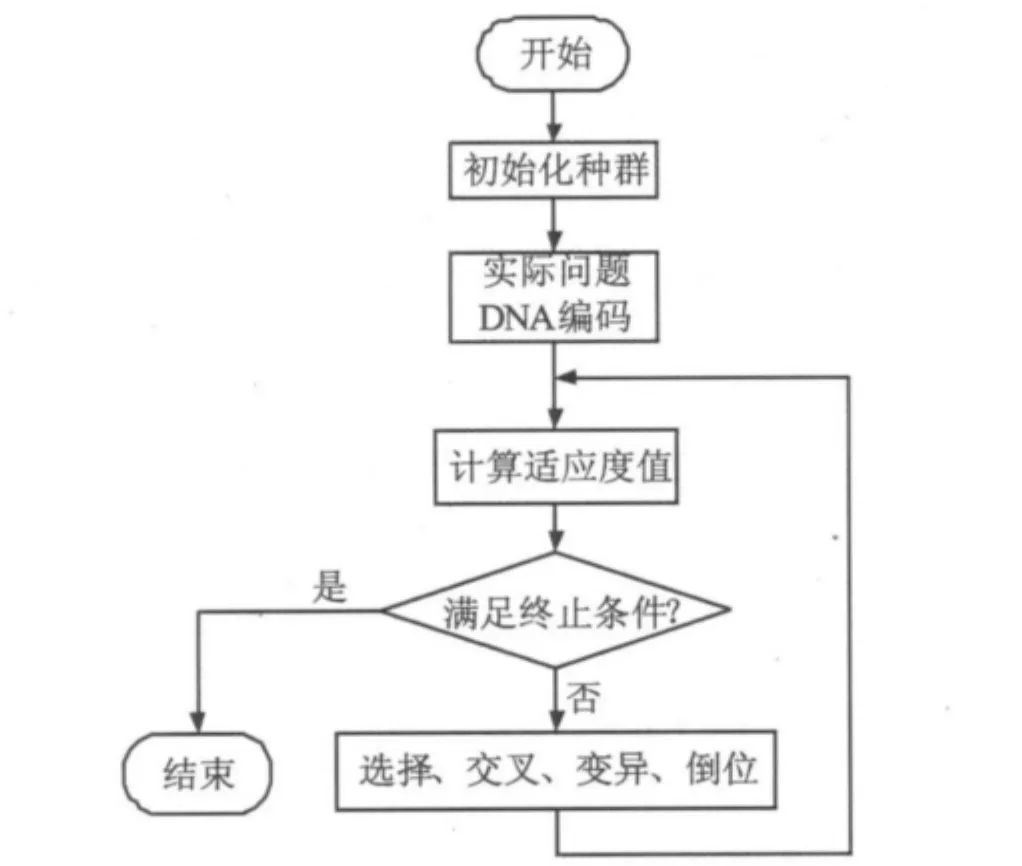
图3 DNA－GA算法流程图Fig.3 Flow chart of DNA－GA method

(1)DNA编码。一个DNA单链由四个不同的符号A，T，C，G组合连成的一个串。数学上，这意味着用字母表∑={T，C，A，G}将信息编码。为了便于计算机操作，规定0代表T，1代表 C，2代表 A，3代表 G。确定控制参数的DNA链编码方式如图4所示。其中每3个碱基组成1个密码子，每3个密码子代表1个P、D参数，总长度为18。每个密码子有64种情况，对应参数的64种组合，在［0，63］区间上的任意1个数，用于问题的求解。

(2)适应度评价。按照编码规则，将DNA种群中的每一个DNA链解码成相应的P、D两个参数值，用适应度函数评价每个DNA链。采用的适应度函数为：Fitness=Const－J (15)式中，Const为一较大正数，保证Fitness的值为正。控制参数编码和解码如图4所示。

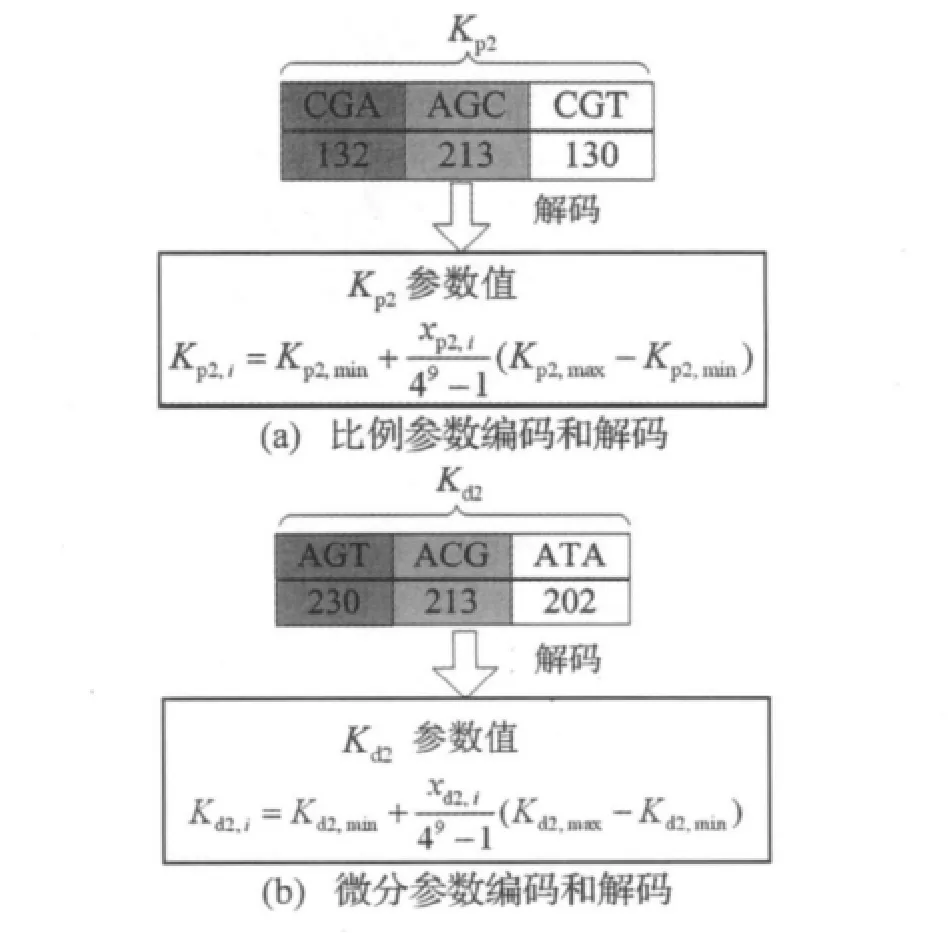
图4 控制参数编码和解码Fig.4 Encoding and decoding of control parameters

(3)选择。采用适应度比例法进行复制，通过选取的适应度函数求得DNA种群中的每一个初始DNA链的适应度值，求出对应每个染色体的复制概率。复制概率与种群数N的乘积为该DNA链在下一代中复制的个数。

(4)交叉。按交叉概率Pc随机选择两条DNA链，随机产生交叉位置进行交叉互换，产生两条新的DNA链。交叉操作如图5所示。

(5)变异。按变异概率Pm从DNA种群中选取若干个DNA链，随机选择DNA链中碱基序列的某一位进行变化。嘌呤替代嘌呤，嘧啶替代嘧啶，即A变成G，或者C变成T。变异过程如图6所示。

图6 变异Fig.6 Mutation

(6)倒位。按倒位概率Pi从DNA种群中随机选取若干个DNA链，再对每个DNA链随机选取两个位置，将这两个位置之间的碱基顺序进行倒位。倒位操作如图7所示。

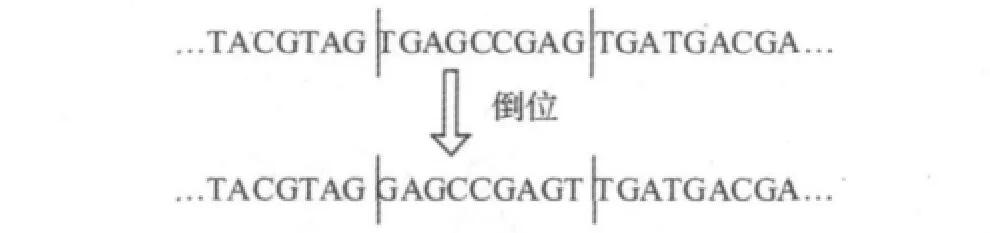
图7 倒位Fig.7 Inversion

3.3 数学仿真

利用系统模型，对DNA－GA自适应整定参数进行数学仿真。设定最大进化代数MaxGen=10，初始DNA种群规模为60个DNA链，交叉概率Pc=0.7，变异概率Pm=0.02，倒位概率 Pi=0.01，Const=20。用4个字符集∑={T，C，A，G}对要优化的控制参数即柔性梁振动抑制的比例系数Kp2和微分系数Kd2进行编码。选取DNA链的总长度为18，每3个密码子代表1个参数。设定Kp2的取值范围为［1，3］，Kd2的取值范围为［0.01，0.03］。

按照公式(15)对DNA链进行适应度评价，选取w1=0.999，w2=0.001。数学仿真时，将 Kp2和 Kd2初始值都设为0，并设定气动驱动定位控制比例增益Kp1=1.0，微分增益Kd1=0.005。仿真时，设定气缸滑块期望位移75 mm，采样时间为5 ms。在0.5 s时加入控制。参数未优化的常规PD控制器的各项参数分别设定为 Kp2=1.0，Kd2=0.005。

仿真结果如图8所示。图8(a)和图8(c)分别为DNA－GA整定的PD控制算法的滑块位移和PCM阀的控制量响应;图8(b)分别表示参数未优化的常规PD和DNA－GA整定的PD控制算法柔性梁的振动响应;图8(d)和图8(e)分别表示DNA－GA整定的PD控制器参数Kp2和Kd2的自适应调节变化曲线。

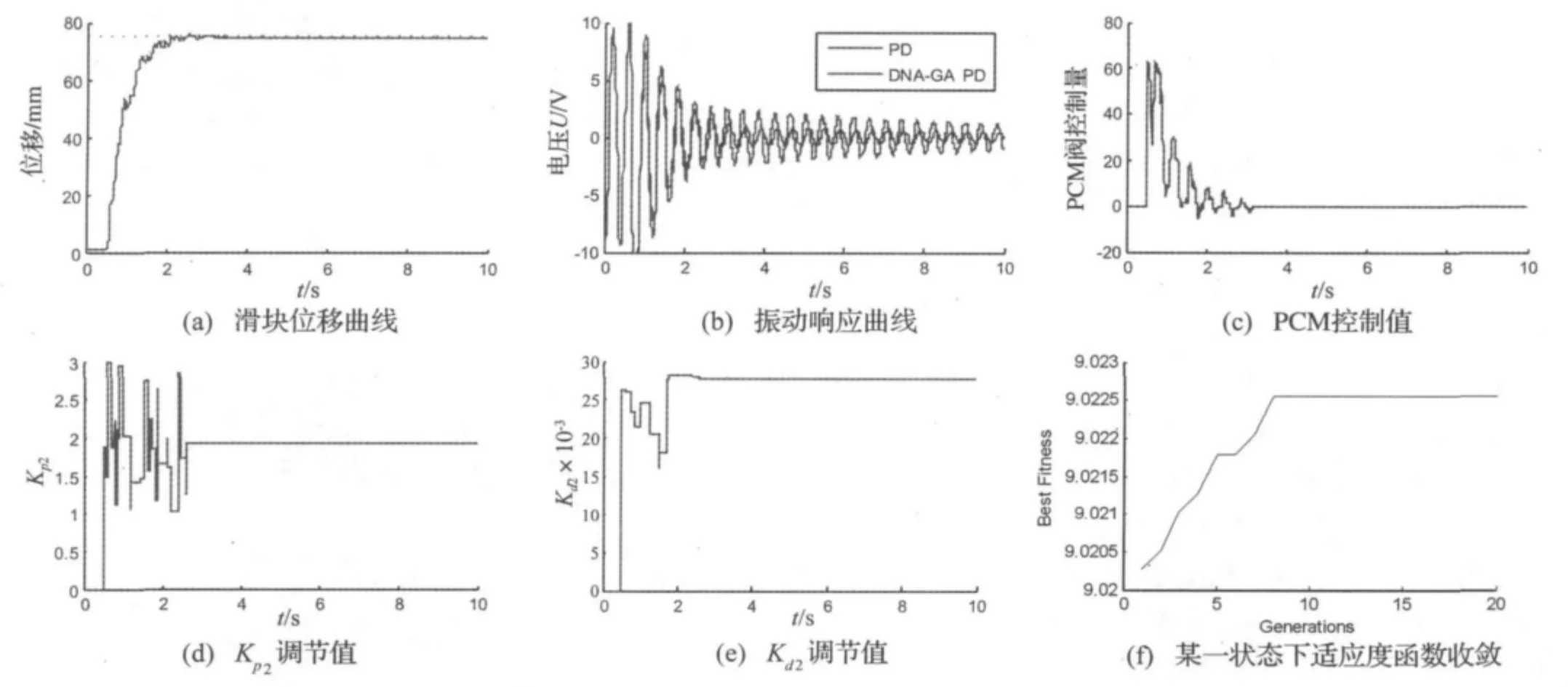
图8 DNA－GA控制数学仿真结果曲线Fig.8 Curves of mathematical simulation results by DNA－GA controller

从图8可知，两种控制算法均能抑制柔性梁振动同时使基座滑块实现定位控制。采用常规PD控制算法后，柔性梁振动的峰－峰值为控制前的24%左右;采用DNA－GA参数整定控制算法后，振动的峰－峰值为控制前的11%左右，控制效果要优于常规PD控制算法。控制量和控制参数按DNA－GA调节变化。

为说明DNA－GA算法能保证收敛，现选取仿真过程的某一采样，并进行20代的进化代数仿真。结果表明，DNA－GA算法在10代的进化代数内能保证收敛。某一采用时间的适应度变化如图8(f)所示。经过反复验证，在任意采样时间的状态可以在10代内收敛，所以试验时为了考虑保证实时性要求，设定DNA－GA算法的迭代次数为10代。

4 实验结果

4.1 气动驱动柔性梁实验系统

气动驱动柔性梁的实验系统如图9所示。气泵(型号：FB－0.017/7)为上海捷豹公司产的静音空气压缩机。如下气动元件为SMC公司生产，相关设备和气动元件及参数：

气动三联件，由空气过滤器(型号：AF30－03)、减压阀(型号：AR25－03)和油雾分离器(型号：AFM30－03)组成;三个气动减压阀(型号：AR2500)，其出口压力分别调为4 bar、3 bar、5 bar分别对应左气腔、背压和右气腔气源压力;气动单向阀(型号：AK2000);气缸型号为CM2RB32－150，缸筒内径为32 mm，行程为150 mm，活塞杆直径为12 mm;气动两位五通阀(型号：VK3120);PCM阀由6个气动两位三通阀(型号：VZ110)分别串联6个气动节流阀构成。滑块导轨型号IKO LRXG15。

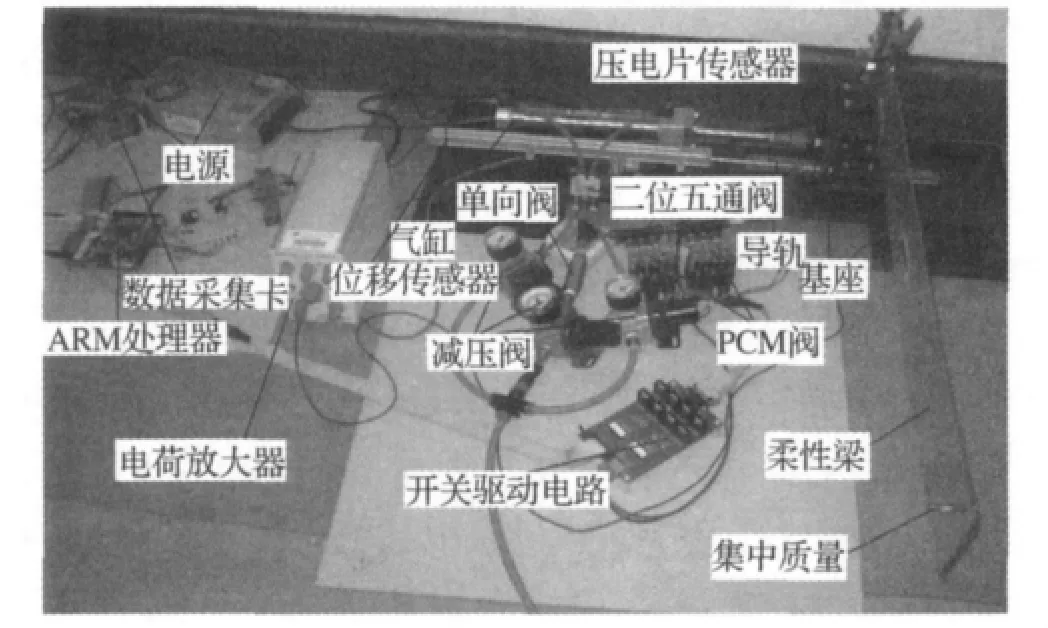
图9 气动驱动柔性机械臂试验装置Fig.9 Experimental apparatus of pneumatic driving flexible manipulator

气缸的滑块位移检测采用KTC拉杆系列线性位移传感器，量程、线性度和重复精度分别为300 mm、0.05%和±0.01 mm。电荷放大器(型号：YE5850)由江苏联能电子有限公司生产，设定其灵敏度档位选择158pC/Unit，输出档位选择0.1 mV/Unit，由12位A/D转换芯片(型号：AD7890)进行模数转换后进入ARM控制器(型号：Mini2440)。开关驱动电路采用场效应开关管，通过24V直流电源驱动控制阀的开关。

柔性梁采用环氧树脂材料，其弹性模量为Eb=34.64 GPa，密度ρ=1 865 kg/m3。柔性梁的悬臂部分尺寸为650 mm×100 mm×1.78 mm。压电片尺寸为50 mm×15 mm×1 mm。末端集中质量为20.6 g。

4.2 柔性梁定位和低频模态振动控制

试验时，气缸滑块期望位移，基于DNA－GA参数整定控制相关参数的选取及范围与3.3节一致。试验时，控制参数的调节是利用系统第一阶模态的模型。

初始状态激励梁的第一阶模态振动，由位移传感器测量滑块位移和由压电片检测到梁的振动信号，经过A/D转换后输入到ARM控制器后通过串行口送到控制计算机，运行控制算法后，再传输到ARM控制器，通过与连接开关驱动电路，输出驱动控制PCM阀和两位五通阀的开关动作。这样控制气缸滑块的运动，实现同时控制滑块定位和柔性梁的振动。试验时，设定采样时间同为5 ms。控制量是在记录试验数据0.5 s后施加的。为了防止滑块在定位点附近的可能产生的极限环震荡现象，设定停止控制条件：在控制算法中设定当PCM值在正负一个码值的持续控制次数超过50次时，将PCM阀设为0，即停止阀的控制动作。

图10为气缸活塞静止时只激励柔性梁的第一阶模态的自由振动响应曲线。图11为参数未优化的常规PD同时进行定位和振动控制实验结果，图11(a)～图11(c)分别为滑块位移、柔性梁的振动响应、PCM阀的控制量。图12为基于DNA－GA参数整定控制实验结果，图12(a)～(f)分别为滑块位移、柔性梁的振动响应、PCM阀的控制量、控制器参数Kp2和Kd2的自适应调节变化。参数未优化的常规PD控制器的各项参数分别设定为Kp=1.0，Kd=0.005。

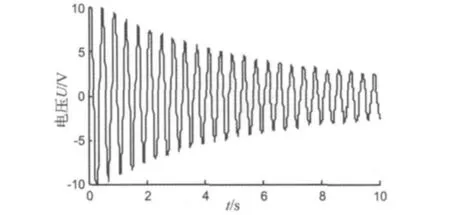
图10 柔性梁自由振动响应曲线Fig.10 Free vibration response curve of the flexible beam

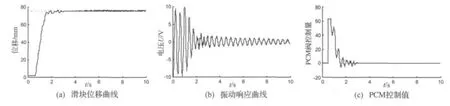
图11 常规PD控制试验结果曲线Fig.11 Curves of experimental results using conventional PD controller

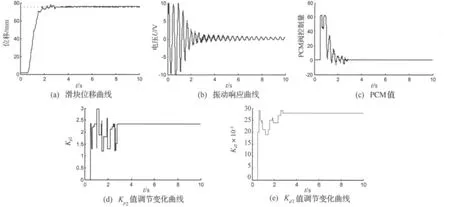
图12 DNA－GA控制试验结果曲线Fig.12 Curves of experimental results using DNA－GA controller

从实验结果图中可以看出，两种控制算法均能抑制柔性梁振动同时使基座滑块实现定位控制。在控制器施加控制量后，控制器在保证实现基座滑块的定位控制同时，控制滑块运动也包括压电传感器反馈控制柔性梁振动;当控制滑块进入平衡点附近后，滑块还在平衡点附近运动来抑制柔性梁的振动，直到满足设定的停止控制条件。从图11(a)和图12(a)可知，采用两种控制算法都能保证气缸滑块最终到达期望位置。从图11(b)可知，采用未优化常规PD控制算法后，柔性梁振动的峰－峰值为控制前的17%左右;从图12(b)可知，采用DNA－GA参数整定控制算法后，振动的峰－峰值为控制前的12%左右，控制效果要优于参数未优化的常规PD控制算法。从图11(c)和图12(c)PCM阀控制量的比较可知，采用DNA－GA参数整定方法要比未优化常规PD控制的震荡幅值大，这说明DNA－GA方法对柔性梁振动的作用大，这也该方法是抑制振动控制效果较好的原因。图12(d)和图12(e)所示为DNA－GA进行PD参数调整，这说明在动态控制过程中参数根据控制性能指标在线自适应整定。

从试验结果和仿真结果比较可知，采用DNA－GA参数整定算法可以有效地实现气动定位和振动控制到较小幅值。仿真结果和试验结果较一致。但试验结果中振动信号含有高阶信号，这是因为气动驱动控制时激励了柔性梁高阶振动模态。因为数学仿真时仅考虑了第一阶模态，所以仿真时没有出现。

在仿真和试验结果中，PCM阀的控制量为负值时表示两位五通阀切换到右位，控制趋势是使活塞向左运动。

由于PCM控制最小通流截面积为一常量和气动系统的非线性，所以仅仅通过采用PCM气动控制方式无法完全抑制低频小幅值振动。今后可以考虑采用气动比例阀代替PCM阀进行控制，还将同时引入梁的压电主动控制，完全抑制小幅值振动。

5 结论

(1)介绍了一种基于PCM方式的有杆气缸驱动控制柔性梁振动系统，并采用主从控制系统来满足运行复杂算法的实时性。

(2)采用DNA－GA进行参数自适应整定控制;用系统模型进行了控制算法的稳定性分析和仿真。

(3)建立了气动驱动控制柔性压电梁试验装置和控制系统，进行了参数未优化的常规PD控制和DNAGA参数自适应整定控制的试验研究。理论分析和试验研究结果表明，提出的气动驱动控制系统及DNA－GA方法可有效抑制柔性梁的大幅值低频模态振动，与参数未优化的常规PD控制相比，两种算法均能实现柔性梁振动抑制和气动定位，但基于DNA－GA参数自适应整定控制算法更好地改善控制系统的动态性能。

［1］ Dwivedy S K，Eberhard P.Dynamic analysis of flexible manipulators，a literature review ［J］.Mechanism and Machine Theory，2006，41(7)：749－777.

［2］ Dadfarnia M，Jalili N，Liu Z Y，et al.An observer－based piezoelectric control of flexible Cartesian robot arms：theory and experiment［J］.Control Engineering Practice，2004，12(8)：1041－1053.

［3］王宣银.PCM气动伺服系统的建模研究［J］.机床与液压，1997，25(4)：20－22+2.

［4］宁 舒.气动位移系统的计算机“PCM”控制初探［J］.液压与气动，1991，(1)：18 －22.

［5］曹青松，周继惠，黎 林，等.基于模糊自整定PID算法的压电柔性机械臂振动控制研究［J］.振动与冲击，2010，29(12)：181－186.

［6］ Ge S S，Lee T H，Zhu G.Genetic algorithm tuning of lyapunov－ based controllers：an application to a single－link flexible robot system ［J］.IEEE Transaction on Industrial Electronics，1996，43(5)：567－574.

［7］ Kim J J，Lee J J.PID controller design using double helix structured DNA algorithms with a recovery function ［J］.Artif Life Robotics，2008，12：241 －244.

［8］Huang Y，Chen X，Hu Y.Optimization for Parameter of PID Based on DNA Genetic Algorithm［A］.Neural Networks and Brain，2005.ICNN＆B'05.International Conference on［C］.2005：859－861.

［9］谢卓伟，石明礼，王 斌，等.气动驱动的柔性机械臂振动控制［J］.华南理工大学学报，2011，39(4)：62－65.

［10］丁永生.计算智能——理论、技术与应用［M］.北京：科学出版社，2004：116－141.

Vibration control of a flexible beam based on pneumatic drive using DNA-GA

QIU Zhi－cheng，WANG Bin，SHI Ming－li，XIE Zhuo－wei
(School of Mechanical and Automotive Engineering，South China University of Technology，Guangzhou 510641，China)

A rod cylinder based pneumatic drive control system was proposed using pulse code modulation(PCM)method.Considering the complexity of the system，the adaptive parameters tuning control using DNA genetic algorithm(DNA－GA)was proposed.The penumatic system and control circuit were introduced.The controllability and the stability of the control algorithm based on fitness function were analyzed by using the system model.The principle of parameters optimization based on DNA－GA was represented.The numerical simulation was carried out.An experimental setup was built up.Experiments were conducted for positioning and vibration suppression simultaneously.The theoretial analysis，numerical simulation and experimental results demonstrate that the adopted DNA－GA self－tuning controller can improve the dynamic performance of control system.The low－frequency large amplitude vibration of the flexible beam is suppressed effectively.

pneumatic drive;piezoelectric flexible beam;vibration control;DNA－GA

TP24

A

国家自然科学基金 (51175181，90505014);华南理工大学中央高校基本科研业务费专项资金资助(2009ZM0148、2012ZZ0060);机器人学国家重点实验室基金(RLO200805)

2011－06－20 修改稿收到日期：2011－09－01

邱志成 男，教授，博士生导师，1973年生