测试数据处理的IGRM模型及其误差分析
2012-02-03李晓峰王建君
李晓峰 王建君
(湖南文理学院电气与信息工程学院1,湖南 常德 415000;广东纺织职业技术学院科技处2,广东 佛山 528041)
测试数据处理的IGRM模型及其误差分析
李晓峰1王建君2
(湖南文理学院电气与信息工程学院1,湖南 常德 415000;广东纺织职业技术学院科技处2,广东 佛山 528041)
针对工程测试试验中试验样本量经常不能达到数理统计方法中所规定的最低样本容量的情况,提出以回归分析模型为试验结果的主规律模型。以主规律模型的拟合结果与系统真值的偏差为对象建立系统残差模型,并将主规律模型与残差模型迭加组成试验结果的集成灰色回归模型(IGRM);同时,给出IGRM模型的建模步骤。经试验与建模验证,IGRM模型对于小样本、贫信息系统具有优异的拟合效果,拟合误差可从原模型的10%左右降到1%以下。
集成灰色回归模块(IGRM) 工程测试 数据处理 误差分析 残差
0 引言
目前,国内外对于工业生产和工程测试中的质量检测数据处理分析方法主要有两大类:一类是采用数理统计方法建立试验对象的回归分析模型;另一类是利用灰色系统理论建立的灰色分析模型。在采用数理统计方法进行分析时,由于存在试验样本的代表性问题,因此要求有较大的样本容量。但在实际工程领域往往存在由于试验方法为破坏性试验的情况,使试验样本量不能满足数理统计方法的“大样本”要求。而灰色模型能够针对小样本、贫信息系统进行分析建模。因此,在日常生产检测与控制中,企业常采用数理统计方法的回归模型进行拟合分析。在样本容量不能满足要求的试验条件下,科技工作者通常采用灰色建模的分析方法[1]。通过试验分析发现,无论是采用回归分析模型还是采用灰色分析模型,分析结果都存在误差,该误差往往不能忽略[2-4]。
对此,本文提出将数理统计方法中的回归分析和灰色系统理论中的系统建模相结合,以建立试验数据处理的集成灰色回归模型(integration grey regression model,IGRM)。试验及建模计算结果证实,IGRM集成模型可大幅度减小模型的拟合误差,从而提高产品质量的在线预测控制精度。
1 回归方程模型
数理统计方法是通过对大量观测(试验)数据的统计分析寻找系统内在规律的数学工具。在需要确定观测值与系统规律所表现的真值之间的关系时,通常采用数理统计中的回归分析(相关分析)法建立观测值与系统真值之间的回归分析模型。在回归模型的建立过程中,通常根据观测(试验)所获得的建模数据作出散点图,然后根据散点图的变化趋势确定回归方程模型的基本形式,利用最小二乘原理导出模型参数,求出相关系数并进行统计假设检验,得出统计结论,从而完成系统回归分析的建模。
设系统有若干组变量观测值(xi,yi),在一定机理作用下它们之间存在某种未知关系。其中,xi为试验观测值,yi为反映系统内在规律的真实值。为了找出系统规律,通常可用含(n+1)个待定系数的n阶多项式来近似表达该未知关系[5-6]:

式中:b0~bn为回归系数,由实测数据根据最小二乘法则确定;x为试验观测值;y^为系统真值的拟合值。式(1)即为回归分析模型。
理论上,任何具有复杂非线性函数规律的试验结果散点图趋势曲线都可以用多项式(1)逼近[3]。当多项式的二次以上项的回归系数为0时,该回归模型为线性回归方程。此外,根据试验数据的散点图变化趋势,也可以采用指数、对数等变化规律的函数去拟合系统规律[7-8]。
2 灰色残差模型
理论上,观测值越多,其所反映的规律就越接近系统的真实变化规律。当对系统进行完全观测(全部试验)时,在观测仪器精度足够高和允许误差范围内,所获得的观测值(试验数据)就是系统的真实情况。实际上,对系统进行完全观测是不现实的。在工程测试中,往往采用按照一定的样本容量要求对系统进行观测或试验。这样采用实际观测值对系统真值进行回归分析就不可避免地存在误差。当样本容量较小时,其回归分析模型的误差较大,甚至超过10%。这在工程拟合计算中是不能容忍的[9]。
灰色系统理论针对少数据、贫信息系统建模。因此,以回归分析模型为系统主规律模型,再通过残差辨识对其误差序列建立灰色残差模型,并利用残差模型对回归分析模型进行补偿,可以最大限度地减小利用观测值拟合系统真值的拟合误差。
所谓残差辨识就是将模型的拟合值与真值间的差建立GM灰色模型,称之为残差GM模型;然后将残差GM模型所获得的预测值加到原来的拟合值上,以提高模型精度。
基于上述思想,将式(1)的结果作为预测值、对应的实际值作为原始值,对其残差建立GM(1,2)模型,把预测结果作为回归预测拟合模型的补偿。这就是基于残差GM(1,2)和回归分析模型集成的灰色回归分析模型[10-11]。
取一原始时间序列:
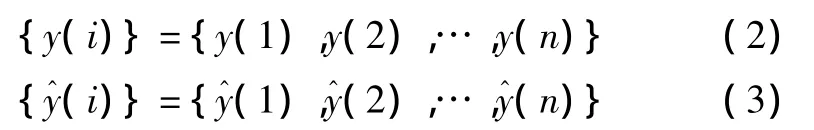
其中,数据序列(2)为实际值时间数列,数据序列(3)为其通过工程检测技术获得的预测拟合值时间数列。其偏差可生成残差初始数列(4):
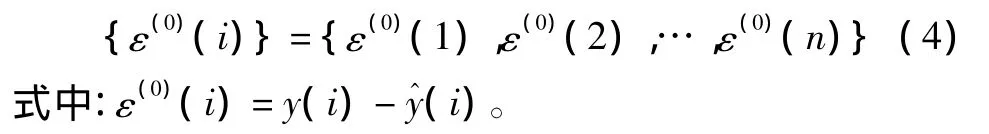
由于残差序列可能为负值,建模前应对序列作非负初始化处理,建模完成后再对建模估计值作非负处理的反运算。对 ε(0)(i)作 m次累加,可生成累加数列:

在灰色系统中,如果残差一次累加后的生成序列{ε(1)(i)}不呈现递增的情况,则不适合建立GM模型。为此必须增加累加次数,使生成序列递增,然后再建立GM模型。根据大量历史生产数据验证,残差的二次累加生成序列开始呈现递增态势。所以,通常取式(6)中的m≤2,即建立二阶的残差GM(1,2)模型。
式(6)中的a(m)、b(m)由最小二乘法求解。记系数向量 A^=[a(m),b(m)]T,则有:
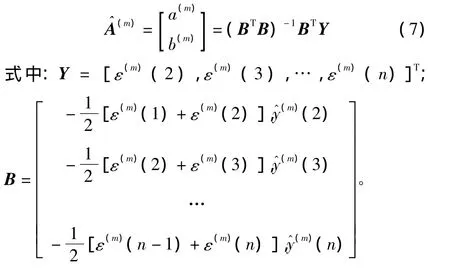
求解出A^(m)后,代入式(6),可解得序列的估计值计算公式的离散模型为:
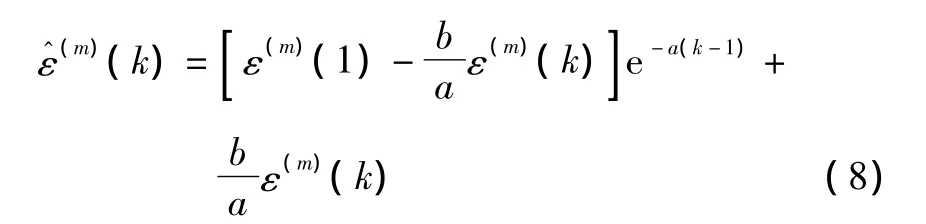
由式(8)所得的输出值为递增值,即对应于m次累加生成的补偿值。要得到真实输出值,还应该还原这些数据,即进行累减生成和非负的反运算处理。
3 IGRM及其建模过程
3.1 IGRM的形式
集成模型以建立回归模型为主规律模型,对其残差序列建立GM(1,2)灰色模型,将残差模型的结果加于回归模型的拟合值之上,对其进行补偿,从而提高模型对系统内在规律的拟合精度。
设ε(0)(i)为拟合值(i)对系统真值y(i)的拟合误差,(0)(i)为采用 GM(1,2)建立的残差模型计算值,则集成模型IGRM可表达为:

式中:y^
1(i)为IGRM的拟合结果。
3.2 IGRM的建模过程
集成模型IGRM的建模过程如下。
①用试验数据作散点图;
②估计散点图趋势并绘制趋势曲线;
③根据趋势曲线选定相近的函数形式或多项式;
④利用试验数据计算回归系数;
⑤将回归系数代入选定的函数式中,完成回归方程;
⑥进行相关分析、方差分析和双总体假设检验;
⑦下统计结论,完成回归分析;
⑧根据回归方程计算回归拟合值;
⑨根据回归拟合值计算残差;
⑩利用残差建立灰色残差模型;
(11)将回归方程和残差模型集成IGRM;
(12)误差校验并完成建模过程。
4 建模实例与误差分析
为验证IGRM模型的拟合精度,以对纺织企业大量使用的传统烘箱进行检测控制系统改造为例,取一组烘箱内相对湿度与被测材料烘干状况数据进行对比观测。试验中,烘箱采用国产Y802型恒温烘箱,对烘箱内小环境相对湿度的测量采用HS1100湿度传感器和NE556芯片组成的湿度测量系统,其测量结果表现为频率Δf;对于烘箱内被测材料的烘干状况,采用随烘燥时间的推移而变化的材料的质量差C表示。显然,材料的质量差越小,表明材料中水分含量越少,即材料越干燥。最后,利用试验数据建立材料质量差和反映烘箱内相对湿度的频率差之间的数学关系模型。这一试验为改进烘箱的检测控制系统提供了依据,并已经申请了国家专利[12]。
试验及建模拟合结果如表1所示。其中,试验材料为羊毛(新疆新毛、澳大利亚国毛)。
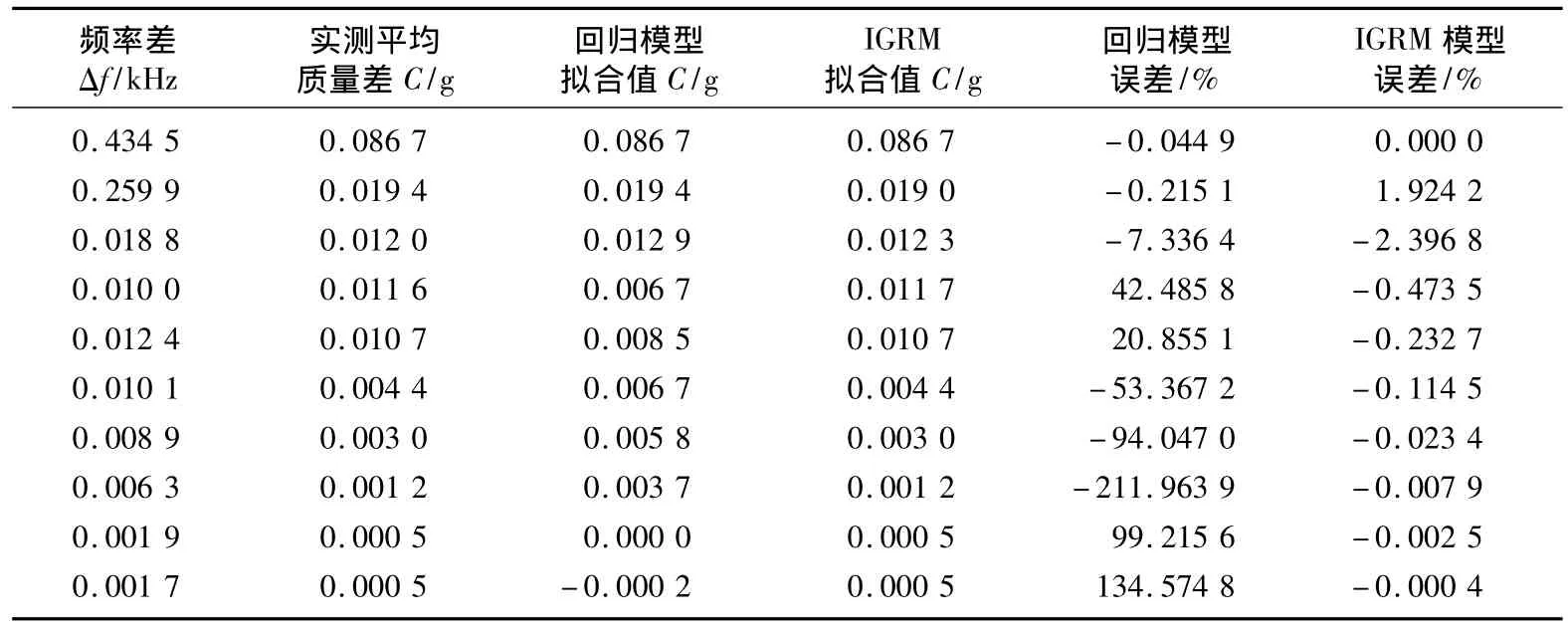
表1 测试数据、建模拟合值及其误差Tab.1 Test data,modeling fitting values and their errors
通过对表1的分析,可以得到如下结论。
①由于系统样本量小于10,属于贫信息系统,不能满足数理统计方法规定的大样本要求,其回归分析模型对结果的拟合平均绝对误差为19.08%,这是工程测试所不能接受的。事实上,在建立回归分析模型时采用了非线性回归分析方法,其模型为4次多项式,复相关系数R也达到了0.9以上,但仍然不能满足仪器改进设计的拟合要求。
②采用IGRM集成模型对结果的拟合平均绝对误差为0.701 4%,拟合精度大幅度提高,且IGRM集成模型的拟合预测误差呈递减的态势,具有明显的规律性,符合灰色系统理论“新息优先”原理。
③将IGRM植入Y802型恒温烘箱的单片机控制系统程序,就可完成烘箱烘燥过程的全自动监控,从而提高测试精度,实现节能改造。
5 结束语
针对工程测试中试验样本为小容量、贫信息的一类工程项目,指出采用回归分析方法存在较大误差,提出了建立基于回归模型和灰色残差模型集成的预测拟合模型IGRM的解决方案,并给出了IGRM模型的基本形式和建模步骤。
为了验证集成模型的效果,以国产Y802型恒温烘箱的监控系统改造为对象进行测试试验和建模。在建模预估过程中,通过实时更新GM模型参数,可使拟合结果更接近真值。试验和误差分析证明,由于残差模型的补偿可以明显减少单一回归模型的拟合误差,使集成模型在试验数据处理中的精度大幅度提高,具有良好的拟合效果。
[1]黄涌波,周孑民,瞿向东,等.铝电解质温度与初晶温度实时测量系统及应用[J].仪表技术与传感器,2008(9):91-92,104.
[2]王建君,李晓峰,王文虎.烘箱空气湿度与纤维回潮率的非线性回归分析[J].纺织学报,2010,31(1):30-33.
[3]李晓峰,王建君.基于非线性回归分析的棉纤维水分快速测量模型[J].数学的实践与认识,2004,34(11):65-71.
[4]陈振林,许晔.基于多元线性回归分析的高精度温度测量[J].电子测量与仪器学报,2000,14(3):11-14.
[5] Wang Zhengxin,Dang Yaoguo,Wang Yemei.A new grey Verhulst model and its application[C]//Proceedingsof 2007 IEEE International Conference on Grey Systems and Intelligent Services,2007:571-574.
[6]熊志刚,吴强.灰色Verhulst模型的样条插值函数的残差修正[J].数学理论与应用,2005,25(1):65-68.
[7]苏变萍,曹艳平.基于灰色系统理论的多元线性回归分析[J].数学的实践与认识,2006,36(8):219-222.
[8]段雄英,黄智慧,廖敏夫,等.基于多元线性回归法的相控开关操作时间的补偿与预测[J].电力自动化设备,2009(7).
[9]任世锦,吴铁军.基于SVM的精确数-区间数回归模型建模方法[J].控制与决策,2006,21(12):1326-1331.
[10]孔玲爽,阳春华,王雅琳.一种基于灰色模型和机理模型集成的质量预测模型及其应用[J].湖南文理学院学报:自然科学版,2007,19(2):68-70.
[11]邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1987.
[12]湖南文理学院.新型纺织纤维水分测试烘箱:中国:ZL200820159126.3[P].2009-09-09.
Integration Grey Regression Model(IGRM)for Test Data Processing and Its Error Analysis
In engineering test experiments,the quantity of experimental samples can barely reach the minimum sample capacity required by mathematical statistic method.Aiming at this phenomenon,the main-law model with the regression analysis model as the experimental results is proposed.The system residual error model is established on the basis of the deviation between the fitting results of the main-law model and the real values of the system,and by superimposing main-law model and residual error model to compose the experimental results of integration grey regression model(IGRM).In addition,the procedures to establish IGRM are given.Through experiments and modeling,it is verified that IGRM possesses superior fitting effects for small sample and poor information system,and its fitting error reduces from 10%of original model to 1%or less.
Integration grey regression model(IGRM)Engineering test Data processing Error analysis Residual error
TP202+.2
A
广东省自然科学基金资助项目(编号:9152841101000001);
广东省高等学校人才引进专项基金资助项目(编号:200886)。
修改稿收到日期:2011-10-24。
李晓峰(1957-),男,2002年毕业于湖南大学控制工程专业,获硕士学位,教授;主要从事计算机在纺织设备与检测技术中的应用方面的研究。
行业信息
