基于数模应用的救护站科学设置
2012-02-01武文杰曹淑方
武文杰,曹淑方
石家庄铁道大学机械工程学院,河北石家庄 050043
1 问题的重述与分析
现有小镇平面图一张,图中方格中的数字是一年中需要救护的次数,图中有一个L型障碍和一个公园障碍。救护车驶过每一个东西向街道要20s,驶过南北向街道要30s,试确定两个救护站,使总的时间最少。如图1所示。
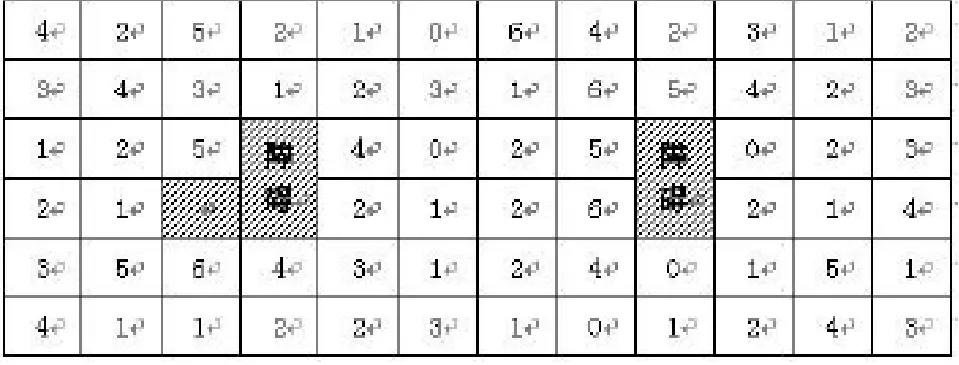
图1 小镇平面图
根据题意,该镇所有街区的需求由A、B两个救护站共同来满足,为了尽量缩短响应时间,某街区一年内所有需求由距离它最近的救护站来满足,而不会舍近求远的选择另一个救护站,即可认为将该镇分为两个“责任区”,分别由A、B来承担。因而我们可以先假设两个救护站的位置,分析每个街区,并判断该街区属于哪个救护站的“辖区”。然后,再考虑两个救护站位置的所有情况,从中找出最优值。
模型一:假设救护站的位置在街角处,而街区的需求全部集中在街区中心。将救护站的位置以及需要服务的街区转化为有限个离散的点,将二者之间的距离转化为两点间的距离,很显然,所有救护站可能的位置是有限个,且最多有13 791×=个位置,而救护站所有可能的位置组合有可能。利用计算机程序,通过有限次的循环和筛选是可以实现的。其次,我们可以先假设救护站的位置不受障碍物的影响,求出最优值之后再进行修订,可以大大减少工作量。通过求解求出的结果是(2,2)、(8,4)两点。而这两点不受障碍物的影响,即为最优值。主要的计算公式为:
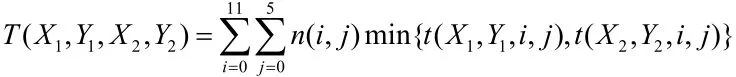
模型二:我们假定需要救护需求沿各街区的街道均匀分布,且救护站仍建立在街角处。街区出现事故的频率平均分布在街区周围的四条街道上,每条街道发生事故的频率与它的长度成正比,而街道的长度由每条街道的响应时间来度量。故可以将街道分为许多长度微元来考虑,通过积分从而求出结果。我们利用微分的思想
2 模型的假设
1)两个障碍中均不需要应急服务,即其一年内的需求次数为零;2)忽略车辆拐弯和过十字街口的时间,仅考虑沿街道运行的时间;3)救护车不能从街区中穿过,只能沿着街道行驶;4)两个应急设施在处理紧急事件时,能力与效率相同,可任选其一;5)救护车每车次只完成一个街区的救护,即在救护车返回的途中在进行第二次救护。
3 模型的建立
3.1 模型一
符号说明:
(注:下文均以坐标表示相应的位置救护站及街区)
1)求某一救护站到某一街区的响应时间:
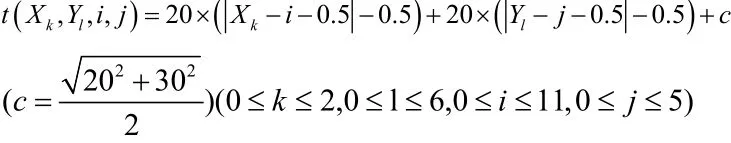
比较(i+0.5,j+0.5)到两救护站的响应时间 ,确定的所属辖区
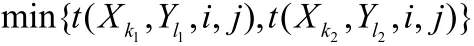
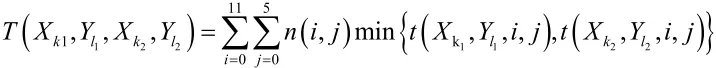
利用穷举法求出最优值
2)让Xk1
3)在求出最优值的前提下,进一步建模求出A、B的“辖区”范围:
3.2 模型二
符号说明:
f( s)=a( i, j)c某段街道CD的需求密度函数
TCD救护站到CD街道的总响应时间
TCD中点救护站到CD街道中点的响应时间
在模型二中,我们假定需要救护需求沿各街区的街道均匀分布,且救护站仍建立在街角处。为了简化计算,我们假象将街道分为两半,即每条街道属于两个不同的街区,救护车会到达同一街区同一点两次,两次的响应时间之和该街道该点的实际响应时间。
某段街道CD的需求密度函数为:
f( s)=a( i, j)c(c为该街区的周长)满足均匀分布将该街道分为许多微元ds
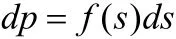
救护站到该街道的总响应时间为:
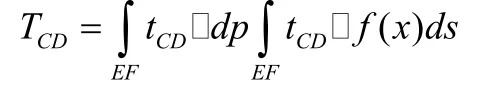
因为街道的需求密度函数为常数,故可以认为该街道的所有需求全部集中到中点处,而其它点的需求为零,该街道总的响应时间不变。
所以有:
当CD为南北向街道时
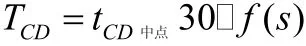
当CD为东西向街道时

而对应的TCD中点则要分四种情况来讨论,这样做的目的是方便编程,在循环过程中不会遗漏,也不会重复
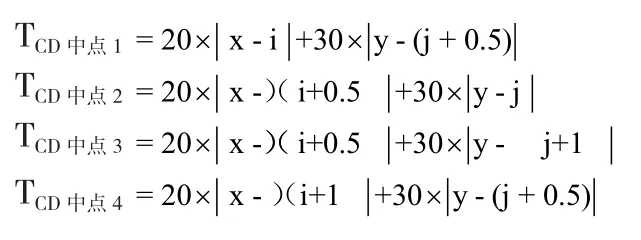
利用计算机对TCD做循环,使TCD取遍街道,即出求出最后的最优解。
4 模型的求解
4.1 模型一
通过运行程序,可以求得满足条件的最优解是(2,2)、(8,4)两点。当边界点取到6个时,已经能确定A、B的辖区边界。这 6 个点是(3,4)、(3,5)、(4,3)、(5,2)、(6,1)、(6,0)下面列表说明:
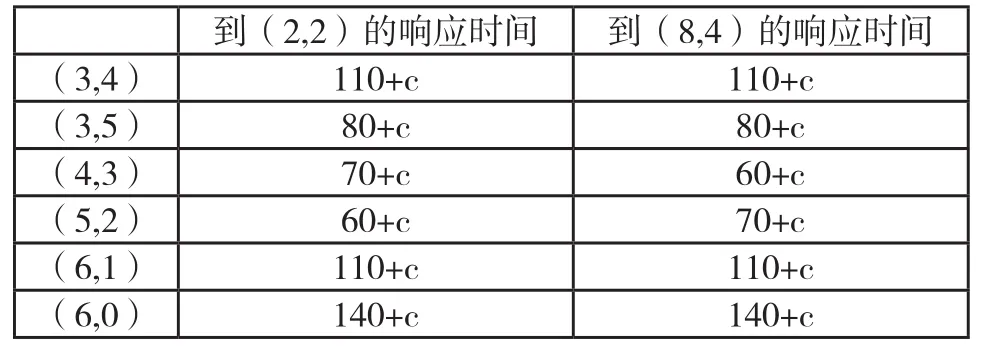
到(2,2)的响应时间 到(8,4)的响应时间(3,4) 110+c 110+c(3,5) 80+c 80+c(4,3) 70+c 60+c(5,2) 60+c 70+c(6,1) 110+c 110+c(6,0) 140+c 140+c
由上表可知,辖区边界的划分方法有2×2×2×2=16种。
4.2 模型二
通过运行程序,可以求得满足条件的最优解是(2,2)、(8,4)两点。
[1]王学军,李静.Visual Basic 程序设计[M].2版.中国铁道出版社,2008,1.
[2]孙海珍,刘宝友,刘响林.概率论与数理统计[M].2版.中国铁道出版社,2003,1.
