一种用于突发性场地污染模拟的解析模型
2012-01-30陈家军全向春
陈家军,王 浩,全向春,文 军
(1.北京师范大学水沙科学教育部重点实验室,北京 100875;2.北京师范大学环境学院,北京 100875;3.新疆水利水电勘测设计院,新疆乌鲁木齐 830091)
0 引 言
随着化学品使用范围日益扩大,在其生产、使用、销售和储运过程中发生泄漏、爆炸和火灾等突发性环境污染事故也相应增多。这类事故发生突然,破坏性大,直接关系到人民群众生命财产的安全,同时也会使人类赖以生存的生态环境遭到破坏。做好突发性环境污染事故的预防、监测、应急处置及善后工作,建立运行有效、行动快速的事故应急管理系统是最大限度减少损失的关键[1]。突发性污染造成的污染场地是潜在的污染源,一旦发生污染事故,不仅后果严重,往往会造成恶劣的社会影响[2]。如美国Love运河污染事件是一起典型的污染场地引起的公害事件,致使大量人群的生命健康受到损害,并引起巨大经济损失[3]。随着中国经济的快速发展与经济结构的调整,污染场地问题备受关注。2004年4月,北京地铁5号线工程宋家庄附近挖掘出含六六六粉、滴滴涕的污泥超过10 000t,后查明此地是北京农药厂原址[4]。
为了更有效地处理各种突发性环境污染事故,减少事故对环境的损害,确保环境尽可能地安全,有必要开发适用于污染场地污染物迁移转化的数学模型。基于模型预测分析一定时间内污染物在包气带及地下水中的迁移动向,开展相应技术评估,采取合理的管理、应对措施并选取适宜的场地污染修复技术,为应急监测与处置工作提供决策支持,确保突发性污染事故的应急监测与处置工作快速有效地进行。目前,国内外已经针对场地污染建立了一些污染物运移的数学模型,其中数值模型[5-8]适用条件广,更为有效,但在应用中对水动力弥散参数和几何数据等要求极高(污染场地范围需有很高的研究程度才能达到要求),操作较为复杂,从而限制了其实际应用。解析模型虽然适用的场地条件不如数值模型广,但所要求的参数较少,模拟计算工作量小,操作使用简单易行,更加符合突发性场地污染模拟预测的要求[9-11]。Beltman等研究了土壤吸附、微生物降解的空间变异性对农药渗漏量的干扰,建立相应的数学模型并预测出这两种因素对农药迁移、降解的影响规律;此外,该模型还考虑了植被对污染物的被动吸附作用[9]。Van Der Zee等根据前人研究建立了饱和带和非饱和带的农药迁移解析模型[12]。但这些研究大多针对难挥发性污染物,模型建立过程中一般都忽略了污染物的挥发性,因此在应用时具有一定的局限性。另外,在突发性污染事故发生初期,若没有遇到降雨,污染物在重力作用下会向地下自由入渗,这种情况也应纳入场地突发性污染模拟的范畴。中国目前针对此类突发性场地污染的解析模型研究还比较匮乏,相关的文献资料非常少见。笔者将建立能够应用于一般性污染场地适用于各种污染物,并且方便使用的包气带、饱和带污染物迁移数学模型并得到相应的解析解。
1 模型假定及概化
1.1 假设条件
若没有降雨发生,污染物发生泄漏前后主要通过自由入渗方式向地下迁移,可采用自由入渗模型模拟污染物的垂向迁移。自由入渗模型中,污染物主要借助重力作用向地下迁移,由于此模型中污染物本身构成了流动相,迁移过程中忽略分子扩散作用,选用一维垂直入渗模型进行模拟。若污染发生时有降雨发生,则污染物随雨水向下迁移。降雨入渗模型中,污染物在包气带中主要借助重力作用向下迁移,迁移过程中伴随植物根系吸收、污染物挥发、分子扩散等多种机制共同作用,因此污染物在包气带中的迁移可使用剖面二维非饱和淋溶模型进行模拟,水平方向仅存在分子扩散作用。污染物进入地下水后随地下水流运移,选用平面二维饱和溶质运移模型进行模拟,除根系吸收外,主要考虑机制与包气带相同。另外,该模型还包括以下假设条件:①污染物在包气带中的运动视为重力作用下的迁移,地表坡度为0;②自由入渗中,仅考虑污染物在包气带的运移,忽略植物吸收作用及生物降解作用,污染物在土壤中的最大饱和度为土壤的有效孔隙度;③若有降雨发生,降雨量平均分配至每天,分子扩散作用在所有区域都发生;④不同包气带位置的土壤质地、水动力参数以及有机物成分与种类均相同;⑤污染物在土壤中的吸附为线性吸附;⑥根系对污染物的吸附为被动式吸收,选用根系被动吸附模型进行模拟,挥发作用只通过孔隙气体进行。
1.2 模型概化
现实中污染源的污染物含量分布不均,污染源也以不规则形状存在。本研究旨在建立一种能够适用各种污染场地模型,因此假定污染源都位于地表位置,形状为一矩形区域,厚度较薄(故不考虑污染源的厚度)。污染物在污染区域内平均分布,各位置污染物含量(质量分数)相同,污染物含量可由污染物泄漏总量计算得到

式中:C为污染物平均含量;M为污染物总量;l1×l2为地面污染源的初始尺寸,l1为初始长度,l2为初始宽度;h为污染物在土壤中的厚度;ρs为土壤密度。
自由入渗模型对自由入渗的概化较为简单,仅考虑垂直一维重力条件下的污染物迁移,以便于污染发生后迅速对污染物的入渗情况进行模拟和预测。
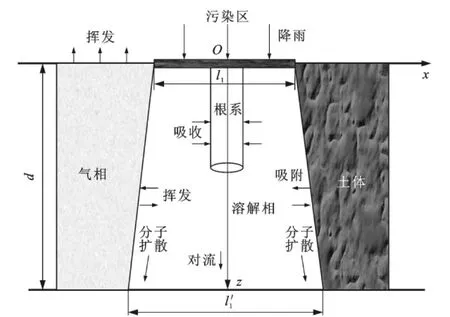
图1 包气带剖面污染物迁移概化Fig.1 Generalization of sectional contaminant migration in unsaturated zone
降雨入渗包气带以及饱和带的模型概化见图1,其中,O为原点,z轴为垂直向下方向。污染物随降雨入渗进入地下土壤,污染物迁移过程中存在于水相,部分污染物被根系吸收进入植物体内,另一部分在重力以及分子扩散条件下发生迁移,迁移过程中不断伴随挥发、吸附作用及微生物降解。残留的污染物继续向地下迁移进入饱和带(图2),污染物扩散至饱和带时初始的污染源尺寸扩大为l′1×l′2矩形区域(l′1和l′2分别为污染羽到达饱和带的长度和宽度),包气带与饱和带界面的污染物浓度作为饱和带的污染源。污染物在饱和带(含水层)的迁移概化见图2,假定含水层厚度较小,饱和带中重点考虑污染物在平面的迁移和扩散,主要考虑的机制有介质吸附、微生物降解、对流弥散作用,扩散作用中包气带只考虑分子扩散,饱和带水流方向取机械弥散,横向则只考虑分子扩散。

图2 饱和带剖面和平面污染物迁移概化Fig.2 Generalization of sectional and planar contaminant migration in saturated zone
2 自由入渗模型
若污染事故发生后短时间内无降雨发生,污染物在重力作用下会以自由态形式缓慢渗透进入土壤,此时可将污染物在土壤中的迁移简化为单相流体的流动,选用流体一维垂向流模型模拟污染物的流动,其基本控制方程为

式中:θc为污染物在土壤中的饱和度;Kc(θc)为污染物相的非饱和渗透系数;Dc(θc)为污染物扩散率;t为扩散时间。
定解条件为


式中:θs为污染物在土壤中的最大饱和度。式(3)的解析解为式中:θc(z,t)为z方向t时刻的污染物饱和度;K-c为土壤渗透系数;D-c为污染物扩散系数。式(4)即为无降雨时突发事故场地污染的自由入渗解析解。
3 降雨入渗模型
3.1 水分运动方程
由降雨强度及根系吸附作用得到土壤包气带孔隙水实际平均流速υu为
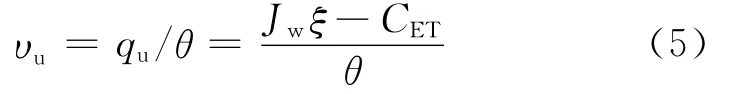
式中:ξ为降雨入渗系数;Jw为降雨入渗速度;CET为植物的蒸腾系数;θ为包气带平均体积含水率;qu为包气带渗流速度。
根据均质各向同性条件得到饱和带孔隙水实际平均流速υs为

式中:H2、H1为2号和1号地下水井的水头;L为两口水井间在地下水流向上的距离;Ks为饱和带的饱和渗透系数;qs为饱和带渗流速度;n为饱和带孔隙度。
3.2 溶质运移方程
考虑生物降解以及土壤对污染物的线性吸附机制,液相污染物的迁移可表示为

式中:C1为土壤污染物含量;ku为污染物在包气带的生物降解系数;Ru为包气带阻滞因子;Dzu和Dxu分别为包气带中z、x方向水动力弥散系数。
3.2.1 包气带模型
(1)根系吸附。若污染场地存在植被覆盖,根系对污染物的吸收速率Rr可以表示为[10]

式中:F为蒸腾流浓度因子;S为植物吸收水分的速率常数。
这样根系区的溶质运移方程可以写成

(2)挥发。挥发途径主要考虑游离态或土壤吸附态的污染物进入空气,挥发速度Rv可以表示为[10]

式中:Dg为土壤-气体扩散系数;Kdu为包气带中污染物土水分配系数。
式(9)可以写为

假设土壤体积含水率不随时间和空间变化,则式(10)可写为

式中:A为总源汇系数;Cu为包气带污染物含量。
式(11)边界条件为

式中:Cu(x,z,t)为包气带点(x,z)在t时刻的污染物含量;C0为土壤初始污染物含量;a为污染源衰减系数。
3.2.2 饱和带方程
饱和带污染物运移的二维方程(平面x,y方向)可以写为

式中:Cs为饱和带中污染物含量;Dxs为饱和带中x方向水动力弥散系数;Dys为饱和带中y方向水动力弥散系数;Rs为饱和带阻滞因子;ks为饱和带污染物生物降解系数。
饱和区溶质运移方程的边界条件为

式中:Cs(x,y,τ)为饱和带点(x,y)在τ时刻的污染物含量;Cu(x,d,τ)为包气带点(x,d)在τ时刻的污染物含量,d为饱和带埋深;C-u为污染羽由包气带到达饱和带时的平均含量。饱和带初始条件取τ时刻当污染羽到达饱和带中的平均含量(图1)。
3.3 溶质运移解析解
3.3.1 包气带模型的解析解
根据包气带的溶质运移模型及边界条件可以求得解析解,其表达式为[13]式中:αzu为包气带z方向水动力弥散度,αzu=Dzu/υu。

3.3.2 饱和带方程的解析解
饱和带方程的解析解C(x,y,t)为
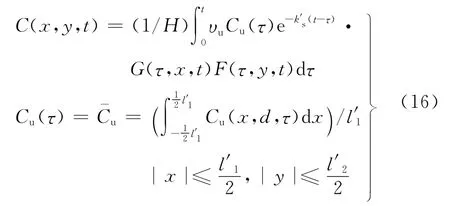

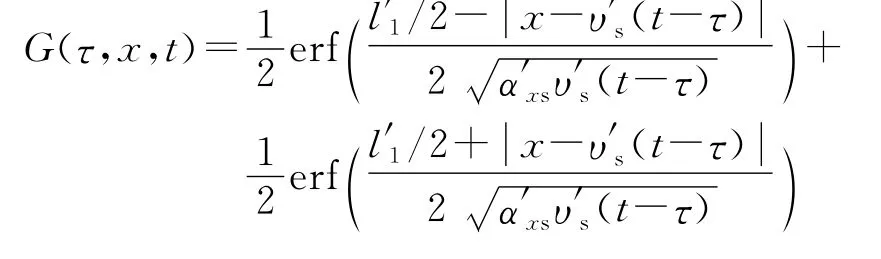


式中:D′xs=Dxs/Rs,D′ys=Dys/Rs,α′xs=D′xs/υ′s,υ′s= υ/R,k′=k/R,均为中间变量;
sssss为污染物在饱和带介质的土水分配系数,ρb为多孔介质密度。
4 案例分析
本研究使用Matlab7.0语言编辑计算机程序,实现整套模型的求解。
4.1 自由入渗
自由入渗模型的建立主要应用于以下两种情形:①突发性污染事故发生后的短期模拟;②中国北方大部分干旱及半干旱地区的场地污染模拟。自由入渗模拟过程中,污染物的最大饱和度为土壤的有效孔隙度(0.3)。选取甲醇作为污染物,模拟计算主要参数见表1。模拟结果以污染物饱和度在深度上的变化规律表示(图3),模拟结果显示甲醇的自由入渗速度非常快,在污染发生21d后污染物就迁移至地表下5.5m处,但自由入渗受污染物自身性质影响较大,如污染物的黏度会直接影响渗透系数,从而改变污染物向下迁移的速度。

表1 自由入渗模拟参数Tab.1 Parameters of free infiltration simulation
4.2 降雨入渗
降雨入渗一般应用于长期模拟,或用于污染事故发生时有降雨条件下的短期模拟。污染发生后首先对包气带污染物的迁移进行模拟,污染源假定为1 000cm的长条区域,重点模拟剖面(x为-1 000~1 000cm,z为-800~0cm)污染物的迁移情况,地下水位埋深假定为800cm,详细模拟参数见表2。表2中a反映了污染发生后,一些自然或人为因素引起的污染物总量减少或含量变化情况,如污染发生后的降雨会引起部分污染物随地表径流迁移至其他地点,同时污染物含量会因降雨而下降,本案例未考虑这些因素。模拟时间为14d,模拟结果以阿特拉津含量随时间的变化等值线表示(图4)。
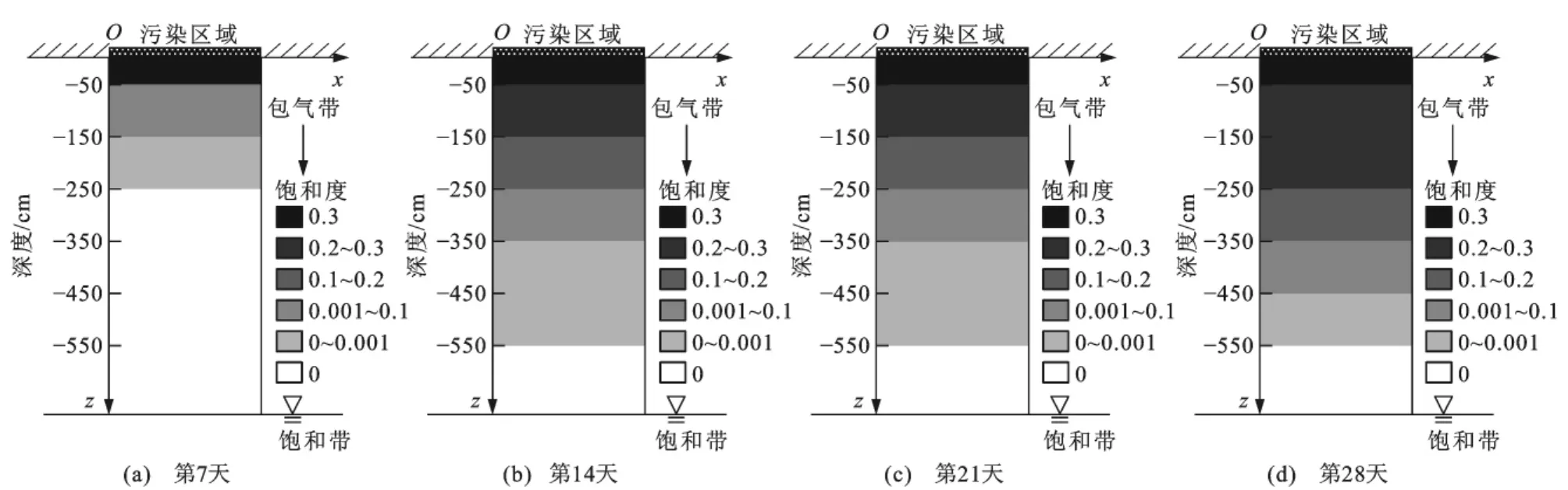
图3 甲醇自由入渗模拟计算结果Fig.3 Results of free infiltration simulation for methanol
包气带阿特拉津含量模拟结果显示,污染物主要在重力作用下向下迁移,同时由于分子扩散作用,污染羽在水平方向也逐渐扩大。由图4可以看出,污染发生14d后污染羽达到饱和带,污染羽的前端含量为29.94×10-6。

图4 包气带降雨入渗阿特拉津含量等值线模拟结果Fig.4 Results of isolines of atrazine contents with rainfall infiltration simulation for unsaturated zone

表2 包气带降雨入渗模拟参数Tab.2 Parameters of rainfall infiltration simulation for unsaturated zone

表3 饱和带参数Tab.3 Parameters for saturated zone
由于包气带的污染物在14d后到达含水层,饱和带的模拟从第14天开始,主要模拟参数见表3。污染发生后第20、30天饱和带的模拟结果见图5。图5描述了污染发生第20、30天时地下水下游100、 300、500、1 000cm处污染物含量的分布情况。图5中y方向距离即为地下水下游位置。模拟结果显示,尽管到达饱和带的污染物浓度比包气带中小很多,但随地下水迁移速度非常之快以至于污染物到达饱和带后6d(污染发生20d)即有污染物迁移至下游1 000cm处。按第14天包气带污染物迁移至饱和带的含量为30×10-6进行计算,污染物在第6天(污染发生后第20天)到达下游1 000cm处的含量为初始含量的0.057%。而饱和带迁移16d(污染发生30d)后,污染物到达1 000cm处的含量占初始含量的1.73%。污染物进入地下水后,迁移的速度主要取决于地下水的流动速度,y方向由于只存在分子扩散,污染物迁移速度相对较慢。因此,在突发性污染事故发生后应及时采取强力有效的措施避免污染物进入饱和带,否则一旦污染物进入含水层后将无限加大后续污染治理的难度。

图5 饱和带降雨入渗阿特拉津含量模拟结果Fig.5 Results of atrazine contents with rainfall infiltration simulation for saturated zone
从以上计算过程可看出,本模型采用的解析求解比数值求解已简单了很多。尽管如此,由于考虑的机制较多(尤其是对于降雨入渗模型),求解过程中所需要的参数仍然较繁杂。实际上对于降雨入渗模型,最重要的参数是污染物的土水分配系数,分配系数可以通过污染物的辛醇-水分配系数或溶解度估算得到,而对于其他参数(如挥发速率因子、生物降解系数以及蒸腾因子)可较易从相关文献或书籍中查得。污染物的水动力弥散系数可通过经验公式计算得到,而其他水文气象参数可直接从当地气象部门获取。针对不同的污染物以及地形条件,可以选择性地忽略模型中的一些机制(如分子扩散、生物降解),这样可以有效简化模型的计算,在突发性污染发生后更及时地进行模拟预测。
5 结 语
(1)针对突发性场地污染,建立了能够应用于一般性污染场地并且适用于各种污染物的包气带、饱和带污染物迁移数学模型,并得到相应的解析解。相比于国外建立的数值模型,该模型具有参数少、操作简单方便的优点。
(2)该模型分为自由一维自由入渗模型和降雨入渗条件下二维污染物迁移模型,入渗模型主要应用于短期模拟或中国干旱、半干旱地区的污染物迁移模拟;降雨入渗条件下污染物迁移二维模型主要考虑的机制包括对流和分子扩散作用、污染物的挥发、植物根系吸收、生物降解、土壤吸附,主要用于长期模拟或突发降雨模拟。
(3)通过案例计算验证了该模型的有效性,模拟结果显示该模型能够快捷、高效地模拟污染物在包气带和饱和带的迁移转化,能较好地适用于突发性场地污染的污染物模拟工作。
[1] 张嵘嵘.城市突发性环境污染事故预警技术支持系统的研究[D].昆明:昆明理工大学,2007.ZHANG Rong-rong.Study on the warning technical support system of environmental pollution accident[D].Kunming:Kunming University of Science and Technology,2007.(in Chinese)
[2] 赵娜娜,黄启飞,易爱华,等.我国污染场地的管理现状与环境对策[J].环境科学与技术,2006,29(12):39-40.ZHAO Na-na,HUANG Qi-fei,YI Ai-hua,et al.Contaminated sites management in China:current status and control[J].Environmental Sciences and Technology,2006,29(12):39-40.(in Chinese)
[3] ZAREMBAMA.Lovecanal:anintroduction[EB/OL].(2004-08-07)[2011-03-12].http://www.onlineethics.org/resources/cases/lcanal.aspx.(in Chinese)
[4] 新京报.北京地铁5号线掘出有毒气体,工期影响尚难定论[EB/OL].(2004-05-01)[2011-03-01].http://news.sina.com.cn/c/2004-05-01/03453180322.shtml.The Beijing News.The toxic gases were found in Line 5of Beijing Subway,so the impact of the gases on construction period was not determined[EB/OL].(2004-05-01)[2011-03-01].http://news.sina.com.cn/c/2004-05-01/03453180322.shtml.(in Chinese)
[5] 张 升,盈尚轩.淮河干流突发性污染数值模拟的应用研究[J].水利科技与经济,2010,16(8):845-846.ZHANG Sheng,YING Shang-xuan.Study on the application of numerical model for the sudden pollution accident in the main stream of Huai River[J].Water Conservancy Science and Technology and Economy,2010,16(8):845-846.(in Chinese)
[6] 张防修,王艳平,刘兴盛,等.黄河下游突发性污染事件数值模拟[J].水利学报,2007,38(增):613-618.ZHANG Fang-xiu,WANG Yan-ping,LIU Xing-sheng,et al.Numerical model for the sudden pollution accident in the lower of the Yellow River[J].Journal of Hydraulic Engineering,2007,38(S):613-618.(in Chinese)
[7] RATHFELDER K M,LANG J R,ABRIOLA L M.A numeri-cal model(MISER)for the simulation of coupled physical,chemical and biological processes in soil vapor extraction and bioventing systems[J].Journal of Contaminant Hydrology,2000,43(3/4):239-270.
[8] CHENG P,WANG C Y.A multiphase mixture model for multiphase,multicomponent transport in capillary porous media II:numerical simulation of the transport of organic compounds in the subsurface[J].International Journal of Heat and Mass Transfer,1996,39(17):3619-3632.
[9] BELTMAN W H J,BOESTEN J J T I,VAN DER ZEE S E A T M.Analytical modelling of pesticide transport from the soil surface to a drinking water well[J].Journal of Hydrology,1995,169(1/2):209-228.
[10] HANTUSH M M,MARINO M A.An analytical model for the assessment of pesticide exposure levels in soils and groundwater[J].Environmental Modeling and Assessment,1996,1(4):263-276.
[11] JIAO J J,TANG Z H.An analytical solution of groundwater response to tidal fluctuation in a leaky confined aquifer[J].Water Resources Research,1999,35(3):747-751.
[12] VAN DER ZEE S E A T M,BOESTEN J J T I.Effects of soil heterogeneity on pesticide leaching to groundwater[J].Water Resources Research,1991,27(12):3051-3063.
[13] CLEARY R W,UNGS M J.Groundwater pollution and hydrology:mathematical models and computer programs[M].Princeton:Princeton University Press,1978.
