多Agent两标的序贯拍卖最优排序策略研究

安阳师范学院 赵 月

多Agent两标的序贯拍卖最优排序策略研究

安阳师范学院 赵 月

序贯拍卖是多Agent系统中资源分配的一项主要机制。考虑现实拍卖环境，放宽基准拍卖模型假设，提出一个公开标的信息的多Agent两标的序贯拍卖模型，分别给出买家Agent在FPSA、SPSA拍卖规则下的竞价策略。根据两标的间不同关系，分析了买家Agent利润和卖家Agent收益的变化情况，由此得到两标的拍卖的最优排序策略。

多Agent序贯拍卖；两标的；公开信息；最优排序策略

多Agent技术在分布式、自由交互、动态环境的系统中具有相当优势。当前，基于多Agent的电子拍卖理论得到众多学者的研究。在多Agent系统中，序贯拍卖变得越来越重要，已成为资源分配的一项主要机制[1]。

Shaheen Fatima在一个买家预算受限、非完全信息环境下的拍卖模型中[2]，分析了买家Agent在第一、第二价格拍卖规则下的均衡竞价策略；Edith在文献[3]中指出为到达收益最大化（revenue-maximizing），卖家Agent应采取的最优拍卖顺序，但这是一个标的只具有私人价值的拍卖模型；Giuseppe给出两个在线序贯拍卖的模型[4]，并分别给出卖家Agent的最优起拍价，但这两个序贯拍卖模型的假设过于严格，并没有考虑标的间的关系，不符合在线拍卖的实际环境。

本文放宽基准拍卖模型假设，提出一个多Agent两标的序贯拍卖模型：D_Riapcv(Double Bids Revealed Information Auction with Private and Common Value)，设定两标的间存在互相影响的关联因子，假设买家Agent不受限制可以参加两次拍卖，分析了两标的之间的关系对买家Agent的利润及竞价策略和卖家Agent的收益有不同的影响。基于两标的间的关系，给出拍卖员为使卖家Agent为获得较高收益的最优标的拍卖排序策略。

1.拍卖模型

两标的D_Riapcv模型定义为M=。其中：

●seller表示卖家Agent的数量，这里研究的是一对多模型，所以seller=1。

●buyer表示买家Agent的数量，buyer=1，2，…n个风险中性的买家Agent。

●R表示买家Agent在不同拍卖规则下的竞价策略，本模型只考虑两种拍卖规则：FPSA和SPSA，取R={FPSA，SPSA}。

●V={VA，VB}，分别表示拍卖中的第一个标的A和第二个标的B的共同价值。

●c={cA，cB}，分别表示标的A和标的B的私人价值。

●Y={YA，YB}表示拍卖员公开两个标的的相关信息。

●a表示两个标的之间的关系，取值{互补，替代，无关性}。

互补、替代的定义如下：

买家Agent i的个人偏好决定标的私人价值的大小，取值独立于信息Y的公开和外部拍卖环境的影响。对标的共同价值的估值则会受到公开信息Y的影响，记二者之间的关系为：

类似于单标的拍卖，为使拍卖员能把买家Agent按照标的的竞价能力排序，须引入下面假设和引理。

据此，买家Agent i可以把共同价值和私人价值二维取值转化成盈余(surplus)的形式把竞价能力表现出来，拍卖员按照每个买家Agent的盈余排序，决定谁能获得标的。

两标的模型考虑以下两点：第一，允许每个买家Agent不受限制的参加两次拍卖。第二，买卖双方都不同程度受到标的间不同关系带来的影响。

假设3：拍卖开始前每个买家Agent分别收到两个标的间私人价值的关联因子a。a在买家Agent之间取独立同分布，取值范围是[αl,αh]。

允许所有买家Agent不受限制地参加两个标的的拍卖，肯定存在某一个买家同时获得两个标的的可能，设买家Agent i同时赢得了两个标的。

则两个标的对于赢家Agent i的私人价值会因为存在关联因子a而变为：

2.买家Agent的竞价策略

两个标的之间存在三种关系：互补、替代、无关系。如果一个买家同时获得两个标的，他的利润在三种不同关系下是不一样的，所以每个买家在标的存在不同关系时的竞价策略也是不一样的。

（1）无关系

如果两个标的之间不存在任何关系，即a=0，买家Agent i对第一个标的提交的竞拍价格、采用的竞价策略，不会对第二个标的的竞价策略和利润分析产生任何影响；同样，是否赢得第二个标的，以及在第二个标的中获益多少，也不会对第一个标的的竞价策略产生影响。这种情况下，买家的竞价策略完全可以按照单标的竞价策略[5]来竞拍。如不赘述。

（2）互补关系

如果两个标的存在互补关系，即a>0。假设买家Agent i只赢得标的A，获得利润PA；如果他只赢得标的B，获得利润PB；如果他同时赢得两个标的，将获得利润为P，则P>PA+PB。

所以每一个买家Agent在参加第一个标的A拍卖时，都会考虑参加第二个标的B的拍卖，并计算从中可能获得的利润，综合分析后才提交第一个标的的竞价；

在给出第一个竞价策略函数前，先来计算买家Agent可能从第二个拍卖中获得的利润。PB是第二个标的赢家的利润：

在第二个拍卖开始前，每一个买家Agent都有可能成为第二个标的的赢家，所以每个买家Agent获得第二个标的的机率是相同的。

1）设拍卖员首先拍卖标的A，第二个拍卖标的B。

则FPSA规则中买家Agent i对标的A的竞价策略函数：

标的B拍卖是最后一个拍卖，没有从后面的拍卖中获利的可能，这时候买家Agent对标的B的竞价策略同单标的拍卖时的竞价策略一样。所以这里只给出FPSA、SPSA两个拍卖规则中买家Agent第一个标的的竞价策略函数。第二个标的竞价的策略请参考单标的拍卖竞价策略[5]。

2）如果拍卖员首先拍卖的是标的B，再拍卖A，则FPSA、SPSA两个拍卖规则中买家Agent的竞价策略分析同上。

（3）替代关系

系统可以接受两种相同格式不同子系统的并行控制信号来完成对机器人内部与外部的并行控制，信号分别来自于机器人语言识别系统和遥控.计算机与声像采集、传输系统结合使得操作者获得较强的临场感.

如果两个标的之间存在替代关系，那么每一个买家可以根据自己的需要来选择是获得标的A，还是获得标的B。显然这种情况下的竞价策略和单标的拍卖时一样。不管拍卖员先拍卖哪个标的，对买家Agent的策略都没有影响。但在第二个标的拍卖时，买家Agent的数量不是n，而是（n-1），因为第一个标的的赢家是不会参加第二个标的拍卖。

3.买家Agent利润和卖家Agent收益

对于买家Agent的利润和卖家Agent的收益分析也从两个标的间的三种关系入手，分开讨论。

（1）无关系

由其竞价策略可知，我们完全可以按照两个单标的模型中的拍卖进行处理。是否获得第一个标的，并不影响买家Agent参加第二个标的的拍卖；同样，由于每一个买家Agent不知道是否参加第二个标的拍卖并能获得胜利，所以买家在提交第一个标的竞价策略时，并不会设想第二个标的拍卖的情况。

所以，在D_Riapcv拍卖模型中，如果两标的之间没有任何关系，买家Agent的利润和卖家Agent的收益和单标的拍卖模型[5]中情况一样。

（2）互补关系

标的间属于互补关系，如果同时获得两个标的，买家Agent将会有更大的利润。不失一般性，假设所有的买家都将参加第二个标的拍卖。买家Agent从第二个拍卖中期望获得利润的机会是均等的。

同单标的模型一样，本章的D_Riapcv模型也符合对称性假设，满足“收益均衡”定理[6]。买家Agent的利润和卖家Agent的收益在FPSA、SPSA两个规则中都是相等的。

1）设拍卖员首先拍卖标的A，第二个拍卖标的B。则标的A拍卖结束，赢家Agent i的利润是：

2）拍卖员首先拍卖标的B，第二个拍卖标的A。则标的B的获胜者Agent i的利润（见公式10）是：

（3）替代关系

如果两个标的间是替代关系，买家Agent只会二选一进行竞拍。这种情况和标的间属于无关系时基本一样。假设拍卖第一个标的有n个买家Agent参加，则第二个标的最多只有（n-1）个买家，两个标的拍卖中的买家Agent利润和卖家Agent收益分析等同于单标的模型的分析。

4.标的拍卖的最优排序策略

拍卖员通过买家Agent利润的顺序统计才能决定两个标的拍卖的顺序。如果拍卖员先拍卖标的A，后拍卖标的B，称为策略1；如果拍卖员先拍卖标的B，后拍卖标的A，称为策略2。首先引入顺序统计离散度的定义。

定义：对于两个标的A和B，如果下面条件成立，则称标的A的利润顺序统计离散度大于标的B的利润顺序统计离散度。否则，则称标的A的利润顺序统计离散度小于标的B的利润顺序统计离散度。

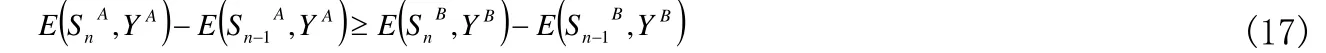
假设4：在下面求解两标的最优拍卖排序策略时，假设标的A的利润顺序统计离散度大于标的B的利润顺序统计离散度。

两标的间存在不同关系，即ai取不同值时，拍卖员采取的排序策略会不同。下面就从ai取不同的值来分别讨论标的拍卖的排序策略。

若式（20）成立，说明这时候策略1和策略2使卖家Agent获得的收益一样大。

综上分析，若式（18）成立，先拍卖标的B，后拍卖标的A，即按照买家Agent利润顺序统计离散度递增拍卖标的，能使卖家Agent获得较大的收益。若式（20）成立，先拍卖标的A，后拍卖标的B，即按照买家Agent利润顺序统计离散度递减拍卖标的，能使卖家Agent获得较大的收益。若式（22）成立，则两标的的拍卖顺序对卖家Agent的收益没有影响。

5.结语

本文构造了一个多Agent两标的序贯拍卖模型D_Riapcv，考虑两标的之间存在不同关系，分别给出买家Agent在FPSA、SPSA拍卖规则下的竞价策略。分析了两标的拍卖的过程中买家Agent的利润和卖家Agent的收益。最后，求解出两标的间的关联因子取不同值时，拍卖员拍卖两标的的最优排序策略。

事实上，现实中拍卖双方面对的问题会更加复杂，例如每次拍卖买家Agent的个人喜好是不尽相同的，那么卖家Agent应如何根据买家Agent的特点有针对性的公开标的属性信息；如果上一个标的拍卖的结果会影响参与下一场拍卖的买家Agent对标的的估价，卖家Agent又该采取何种拍卖策略以提高期望收益等问题；这些都将作为我们今后要考虑的问题。

[1]Giuseppe Lopomo,Leslie M.Marx and Peng Sun,Bidder collusion at first-price auctions[J].Review of Economic Design2011,15(3):177-211.

[2]柴玉梅,赵月,王黎明.基于信息相似度分类的多agent公开信息拍卖模型[J].计算机应用研究,2009,26(12):4532-4535.

[3]Milgrom.P.R,Weber,R.J.A Theory of Auctions and Competitive Bidding[J].Econometrica,1982,50:1089-1122.

赵月（1982—），男，河南安阳人，硕士，现供职于安阳师范学院，主要研究方向：分布式人工智能。