一种改进的线性图像插值算法
2012-01-29高放赵杰
高放,赵杰
(河北大学 电子信息工程学院,河北 保定 071000)
随着计算机图形学与数字图像处理技术的发展,图像插值技术也应运而生。所谓图像插值就是一个图像数据再生的过程。从硬件上着手图像插值,可以获得较高的图像质量,但需要付出较昂贵的代价,基于此,从软件方面进行改进,则显得更有意义。
传统的图像插值方法有最近邻插值,双线性插值,双立方插值等[1]。最近邻插值算法简单,运算速度快,但插值质量差,容易出现锯齿、方块效应;双线性插值虽然减轻了锯齿和方块效应,但它的平滑作用会使图像细节产生退化,图像变得模糊;双立方插值较好的改进了这一点,但运算量巨大,不适合实时应用[2]。近年来许多学者又提出了一些基于边缘和梯度[3-4]的图像插值算法,取得了好的视觉效果,但是计算量都很大。笔者提出了一种改进的线性插值算法,根据待插值点所处的位置选择合适的已知点进行插值,计算简单,经实验证明,该算法能有效的保持图像边缘,提高了图像的质量。
1 本文算法
本文对一幅图像的插值分为两步,先进行矩形插值,再进行梅花插值,即先插值行列和为偶数的点,再插值行列和为奇数的点[5]。在每步插值过程中将待插值点进行分类,对不同类的待插值点分别选取最佳的已知点进行插值。
1.1 矩形插值
一般情况下,一幅图像可以划分为几个不同的区域,不同的区域有着不同的特征,就灰度图像来说,同一区域内各像素的灰度值相近,不同的区域间像素灰度值差异较大。在一个区域与另一个区域之间存在着边缘。所谓图像边缘就是一个区域与另一个区域的分界线,表明一个区域的终结和另一个区域的开始。如果一幅图像中存在边缘,则边缘是“成对”的,如图 1(a),A1,A2为区域 A 内的两个像素点,B1,B2为区域B内的4个像素点,由对边缘的定义可知,A1,A2表示区域A的终结,为区域A的边缘,B1,B2表示区域B的开始,为区域B的边缘,即A1,A2与B1,B2都为边缘,所以说边缘是“成对”的。另外,图1(a)中的 B2,B3与C1,C3为一对斜边缘。
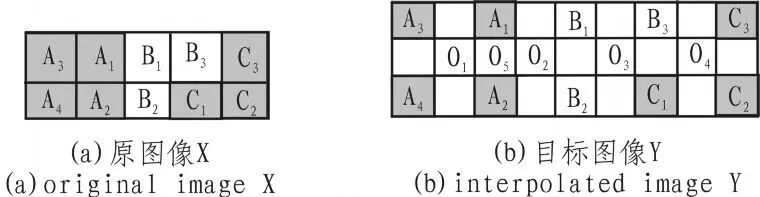
图1 原图像与目标图像Fig.1 Edges in the image
首先假设原图像为X,如图1(a),插值后的目标图像为Y,如图1(b)。本文将待插值点分为3类,下面分别介绍了这3类待插值点的特征,并且分析了采用传统的双线性插值法对其插值结果的影响。
第1类待插值点处于一个区域的内部,以O1为例。由图可知O1处于区域A的内部,其对应原图像中的4个相邻点分别为 A1,A2,A3,A4,令其灰度值为 f(Ai),i=1,2,3,4,由于它们同属于区域A,所以其灰度值相近,因此,O1四邻域内任何方向(垂直、水平、两个对角方向)上的像素灰度差值都较小。对其进行双线性插值如下:
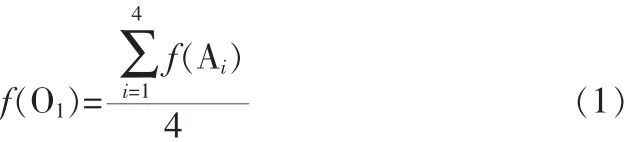
由(1)式可知,对O1的插值结果也表现为区域 A的特征。因此,此类待插值点适合采用传统的双线性插值法。
第2类待插值点位于某一区域的边缘上。此类分两种情况即位于45°对角线边缘上或135°对角线边缘上,在此以位于区域C的45°对角线边缘上的O4为例,其4个相邻点分别为 B3,C1,C2,C3,由于 B3与 C1,C2,C3属于不同的区域,故沿45°度对角线方向上的像素灰度值差值较小,而沿135°方向上的像素灰度值差值较大(当待插值点位于135°对角线边缘时特征正好相反),对其进行双线性插值:
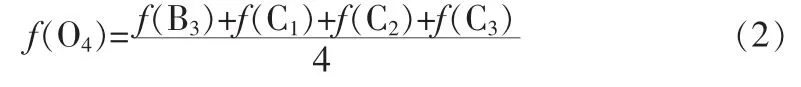
由式(2)可知,O4的灰度值由区域B和区域C的像素点灰度值共同决定,使得O4混合了区域B和区域C的特征,而O4本属于区域C,因此平滑掉了区域B,C间的差异,造成了边缘模糊。由此可见,采用传统的双线性插值对此类待插值点的插值效果并不理想。
第3类待插值点位于两个区域之间。此类也分两种情况即位于两个水平区域之间或两个垂直区域之间,在此以位于2个垂直区域A,B之间的O2为例,其4个相邻点分别为A1,A2,B1,B2。沿垂直方向上的像素灰度差值都很小(当位于两个水平区域之间时沿水平方向上的像素灰度差值都很小),其他任何方向上的灰度差值都较大。对其进行双线性插值:
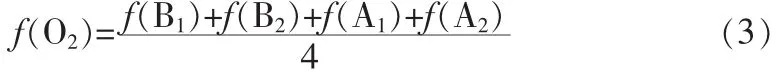
同样,O2混合了区域A和区域B的特征,平滑掉了区域A,B间的差异,造成了边缘模糊。对此类待插值点进行双线性插值的效果也不理想。
由上面的分析可知,采用传统的双线性插值法对第2类与第3类待插值点进行插值时之所以会产生边缘模糊,原因在于插值时选取了不同区域的已知点,如果只选取同一区域的已知点,即待插值点的灰度值只由一个区域的像素点灰度值决定就会避免这种现象。本文基于此进行了改进,先计算待插值点四邻域内各个方向上的灰度差值,通过与阈值T比较来判断该点属于哪一类,若为第一类则直接双线性插值;若为第二类则先判断边缘方向,只沿该边缘方向插值;若为第三类则先判断区域方向,取灰度差值最小的那个区域中的两个已知点进行插值。具体算法如下:设待插值点为Y2i+1,2j+1,取其在原图像中对应的2×2邻域,如图2,分别计算其水平、垂直、两个对角线方向上的像素灰度值之差,如式(4)。
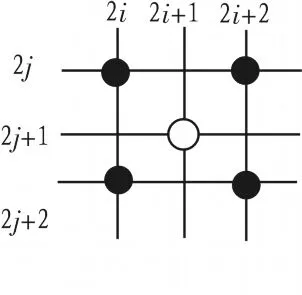
图2 待插值点的2×2邻域Fig.2 2×2 Neighborhood of Interpolated Pixel

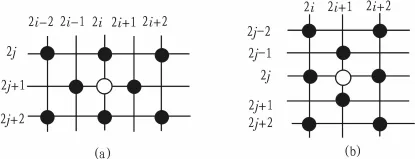
设Dmax=MAX(Di)Dmin=MIN(Di)i=h1,h2,v1,v2方法步骤如下,其中T为预先设置的阈值。If Dmax %以下待插值点都为第3类 矩形插值后,利用原图像已知像素点与矩形插值中计算出的像素点对行列和为奇数的点进行插值。行列和为奇数的点有两种:位于偶数行奇数列上的点(如图3(a)中的点(2i,2j+1))和位于奇数行偶数列上的点(如图 3(b)中的点(2i+1,2j))。本文以点(2i,2j+1)为例来说明。步骤同矩形插值,先求出待插值点四邻域各方向上的像素灰度差值,通过阈值判断进行分类,然后选取合适的点插值。具体步骤如下: 图3 行列和为奇数的点Fig.3 Pixels whose sum of line and column is odd number 采用本文的算法与双线性法和双立方法分别对灰度图像lena和pepper用matlab[6]进行同样倍率的插值,比较插值后原图像与插值后图像的峰值信噪比(PSNR)。PSNR[7]反映了插值图像与原图像相符合的程度,其值越大越好,它的定义如(6)式。 其中,f(i,j),g(i,j)分别对应原图像和插值图像在点(i,j)上的取值;M、N 分别是原始图像中行(i)、列(j) 像素点的个数;L是图像中灰度值的取值范围,对8比特的灰度图像而言L=255。比较结果如表1所示。 表1 不同插值算法的PSNR比较Tab.1 Test result of photoelectric conversion circuit 图4显示了对lena灰度图像分别用双线性、双立方和本文算法进行2倍插值后的图像视觉效果。从图中可以看出,用双线性插值法得到的插值图像存在边缘模糊的现象,双立方法有显著的改进。本文算法视觉优于双线性算法,与双立方算法效果相当,但计算量远远小于双立方法。 图4 对Lena采取3种插值方法的效果图Fig.4 Visual effects of lena 本文提出了一种改进的线性插值算法,先根据待插值点所处的位置对其进行分类,然后根据类别选取最佳的已知点进行插值。实验结果表明,该算法运算速度快,插值效果与双立方插值效果相当,改进了传统双线性插值边缘模糊的现象,插值生成的图像更加清晰,有较好的视觉效果。 [1]符祥,郭宝龙.图像插值技术综述[J].计算机工程与设计,2009,30(1):141-144.FU Xiang,GUO Bao-long.Overview of image interpolation technology[J].Computer Engineering and Design,2009,30(1):141-144. [2]陈建辉,王博亮,徐中佑,等.一种自适应最大相关性数字图像插值算法[J].厦门大学学报:自然科学版,2005,44(3):355-358.CHEN Jian-hui,WANG Bo-liang,XU Zhong-you,et al.An adaptive max-relativity interpolation algorithm for digital image[J].Journal of Xiamen University:Natural Science,2005,44(3):355-358. [3]张美玉,王孝通,徐晓刚.改进的图像自适应梯度插值[J].中国图像图形学报,2009,14(5):853-858.ZHANG Mei-yu,WANG Xiao-tong,XU Xiao-gang.An improved adaptive image interpolation with gradient features[J].Journal of Image and Graphics,2009,14(5):853-858. [4]谢美华,王正明.基于图像梯度信息的插值方法[J].中国图像图形学报,2005,7(10):856-861.XIE Mei-hua,WANG Zheng-ming.Image interpolation based on gradient[J].Journal of Image and Graphics,2005,7(10):856-861. [5]党向盈,吴锡生,赵勇.基于边缘最大相关性的快速图像插值算法[J].计算机应用,2006,26(12):2880-2883.DANG Xiang-ying,WU Xi-sheng,ZHAO Yong.Fast image interpolation algorithm based on edge-directed max-relativity[J].Computer Applications,20076,26(12):2880-2883. [6]胡晓军,徐飞.Matlab应用图像处理[M].西安:西安电子科技大学出版社,2011. [7]王会鹏,周利莉,张杰.一种基于区域的双三次图像插值算法[J].计算机工程,2010,36(19):216-218.WANG Hui-peng,ZHOU Li-li,ZHANG Jie.Region-based bicubic image interpolation algorithm[J].Computer Engineering,2010,36(19):216-218.
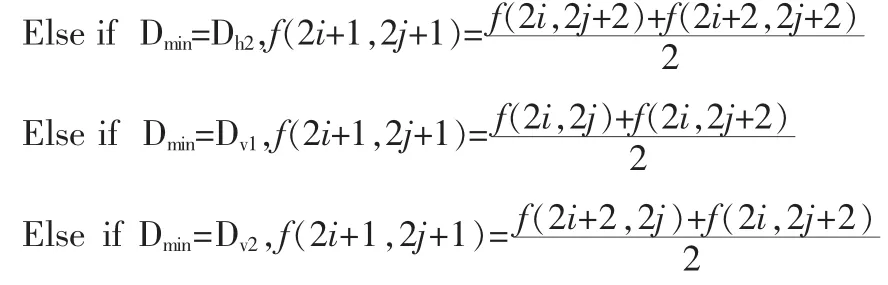
1.2 梅花插值

2 实验分析
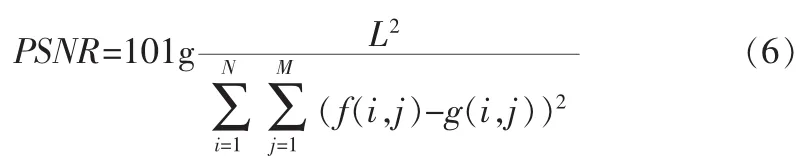


3 结 论
