意料之外 情理之中——2012年浙江省数学高考数列题赏析

●

(宁波中学 浙江宁波 315100)

意料之外情理之中
——2012年浙江省数学高考数列题赏析

●周丕芬王晓明

(宁波中学 浙江宁波 315100)

例1设Sn是公差为d(d≠0)的无穷等差数列{an}的前n项和，则下列命题错误的是 ( )

A.若d<0，则数列{Sn}有最大项

B.若数列{Sn}有最大项，则d<0

C.若数列{Sn}是递增数列，则对任意n∈N*，均有Sn>0

D.若对任意n∈N*，均有Sn>0，则数列{Sn}是递增数列

(2012年浙江省数学高考理科试题)

例2设公比为q(q>0)的等比数列{an}的前n项和为Sn.若S2=3a2+2,S4=3a4+2，则q=________.

(2012年浙江省数学高考理科试题)

例3已知数列{an}的前n项和为Sn，且Sn=2n2+n，n∈N*;数列{bn}满足an=4log2bn+3,n∈N*.

(1)求an,bn；

(2)求数列{an·bn}的前n项和Tn.

(2012年浙江省数学高考文科试题)

试题赏析数列是高中数学的重要内容，是学习高等数学的基础，是高考重点考查的内容之一.2012年的浙江省数学高考数列题，与2011年相比，文科继续保持了原有的要求及风格，以一个大题的形式出现；而理科虽说考试要求不变，却改变了出题的风格，从2011年的考查一个大题又回到了之前的只考小题不考大题的风格，考查了2个小题，分别以选择题和填空题的形式出现.这种形式的改变，与省考试院提供的参考卷对比，的确是在意料之外，但联系新课程背景之下数列的教材内容，却也在情理之中.

从试题上来看，数列主要考查等差、等比数列的概念以及通项公式，等差、等比数列的求和公式等基础知识，同时考查运算求解能力、函数与方程思想等等，以简约的语言道出了一个真谛“平平谈谈才是真”！

1 平凡中见知识要求

试题关注对数列基础知识的考查，力求全面又突出重点，均以等差、等比数列——数列知识中作为支撑的重点内容作为背景来加以命题，并以考查其相关知识构成数列试题的主体，注重知识点之间的内在联系和知识的综合性，要求学生能从整体出发考虑问题，体现其思维价值，使对数列基础知识的考查达到必要的深度.

如例2，考查的是等比数列中的基本量运算，常见解法如下：

解法1基本量思想

将S2=3a2+2，S4=3a4+2转化成用a1,q表示的式子,即

两式作差，可得

a1q2+a1q3=3a1q(q2-1)，

即

2q2-q-3=0，

解得

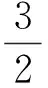
解法2整体思想

考虑所求的q为一个比值，直接将S2=3a2+2,S4=3a4+2两式作差，得

a3+a4=3a4-3a2，

两边同除a2，得

2q2-q-3=0，

下同解法1.

解法3公式代入法

若q=1，则有

方程组无解，故q=1不满足条件.

若q≠1，则有

解出相应q的值.

从解法比较来看，解法3最为常规，但无疑运算量大，此题明确要求考生从整体出发，能够对所需解决的问题加以分析，并寻求适当的途径加以解决.

2 平凡中见能力要求

试题关注《2012年浙江省普通高考考试说明》中强调的“以能力立意”，即以数列的相关知识作为载体，从数列问题入手，侧重体现对数列知识的理解和应用，尤其是综合应用和灵活应用.

如例1涉及到了递增数列的概念、数列中的最大项及等差数列的前n项和公式的活用等相关的基础知识、基本技能，常见解法如下：

解法1关注数列与函数的联系

由等差数列知识，可设

由二次函数的性质知选项A,B,D正确，而选项C只能得到对称轴的范围限制，并不能得到相关结论，故选C.

解法2利用相关概念及性质

由d<0，可知必存在m，使得当n≥m时，有an<0，即当n≥m时，有Sn

由等差数列的前n项和数列{Sn}有最大项，可设{Sn}的最大项为Sm，则

从而

即

am-am+1≥0,

即

d≤0.

又已知d≠0，则有d<0，可知选项B正确.

由等差数列的前n项和数列{Sn}为递增数列，则当n≥2时，Sn-Sn-1>0，即an>0，但无法保证a1>0，即无法保证S1>0，故选项C不能确定.

选项D由任意n∈N*，均有Sn>0，知a1>0，且d>0(可用反证法进行思考)，则有an>0，故数列{Sn}是递增数列，则选项D正确.故选C.

解法3特殊数列验证法

举出反例：-1，0，1，2，3，…满足数列{Sn}是递增数列，但是Sn>0不成立．故选C.

此题用来检测知识的迁移水平，从而检测出个体的理性思维的广度和深度，体现能力要求.

3 平凡中见个性品质要求

试题关注思想价值立意，注重通性通法，淡化特殊技巧，注意数学概念、数学本质和解决数学问题的常规方法，体现在试题的情境熟、入口宽、有层次，有利于学生在公平的背景下展示真实水平，体现考生个体的情感、态度和价值观，表现出考生的思维习惯是否谨慎等.

如例3，解法如下：

(1)由Sn=2n2+n，得

当n=1时，a1=S1=3.

当n≥2时，

an=Sn-Sn-1=

2n2+n-[2(n-1)2+(n-1)]=

4n-1(n∈N*).

由an=4log2bn+3，得

bn=2n-1(n∈N*).

(2)由第(1)小题知

anbn=(4n-1)·2n-1(n∈N*)，

从而

Tn=3+7×2+11×22+…+(4n-1)·2n-1,

即2Tn=3×2+7×22+11×23+…+(4n-1)·2n,

因此2Tn-Tn=

(4n-1)·2n-[3+4(2+22+…+2n-1)]=

(4n-5)2n+5,

故

Tn=(4n-5)2n+5(n∈N*).

试题要求考生以平和的心态作答，强调严谨性，在例3中主要表现为已知Sn求an问题中的分段讨论.联系以对数作为背景的运算，加强试题的广度，运用错位相减法求和，考验运算能力及心态.

与其他省份的数列试题相对比，浙江省数学高考的数列题难度中等.纵观各省，对于数列的教材内容有差异，考试要求有所不同，考查的风格也各有特色.但总体来说，等差、等比数列是永恒的背景，基本量运算是不变的旋律，与其他知识的结合是发展的方向，有关的应用问题则是创新的源泉.