预应力混凝土斜拉桥考虑剪力滞效应的主梁应力监控

武志军

(中铁十局集团有限公司,济南 250000)

1 概述

大跨度桥梁的建造,为保证施工质量和安全,使桥梁的线形与内力达到设计的理想状态,对整个施工过程进行监控,是不可缺少的措施之一。对于预应力混凝土斜拉桥这样复杂的高次超静定结构也不例外。预应力混凝土斜拉桥主梁多为宽翼板薄壁受弯构件,在其施工过程中,结构体系多次转换,主梁的受力状态频繁变化,因而其剪力滞效应并不是一成不变的,这不但给悬臂施工中的结构安全造成危害,也给主梁的应力监测带来困难,因此在施工过程中考虑剪力滞效应的应力监测是必要的。

剪力滞现象在桥梁结构中的研究已有丰硕的成果[1-8]。在桥梁设计中已经考虑了剪力滞效应。例如国内设计规范中采用“有效分布宽度”法、弯矩抛高法来处理剪力滞效应问题[10]。但在大跨度桥梁的施工监控中,剪力滞效应的影响程度与变化规律,以及如何考虑剪力滞效应这一问题的研究较少。

徐州市和平路斜拉桥是一座独塔的预应力混凝土斜拉桥,跨径为176 m+192 m,采用塔、墩、梁固结体系。主梁采用肋板式预应力混凝土结构,桥面宽28.0 m。主梁两侧高2.5 m,顶宽28.0 m,底宽26.0 m,梁顶设2%的人字坡。高跨比1∶76.8；宽跨比1∶6.9；标准主肋底宽2.0 m,桥面板厚0.29 m,主梁设计为C60预应力混凝土。主桥标准段索距6 m,现浇段索距3 m。桥塔为H形,索塔高100.5 m。拉索采用扇形双索面密索体系,共116根斜拉索,梁上标准索距为6.0 m,在边跨加密区内为3.0 m。桥梁布置示意如图1所示。在该桥的施工监控中,应用文献[1]所提出的每节点两个剪力滞自由度的剪力滞效应梁段有限梁理论,对悬臂施工过程中主梁的应力进行了监测。

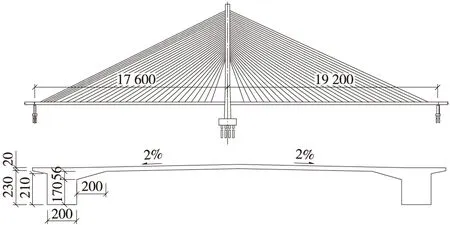
图1 和平路斜拉桥立面和主梁截面示意(单位：cm)

2 两剪滞自由度的有限梁段法

求解剪力滞效应的有限梁段法,最初仅考虑每节点一个剪力滞自由度[2,3],其不足之处是不能适应全部的剪力滞分析边界条件。文献[1]提出的考虑每节点两剪力滞自由度的剪力滞效应有限梁段法,结合杆系有限元方法,可适用各种边界条件,且简单方便。

考虑两剪力滞自由度的剪力滞效应有限梁段法,是基于变分法的微分方程和边界条件,由微分方程的齐次解引入边界条件而导出。其微分方程和边界条件为

(1)

(2)

(3)

式中，I为断面形心主惯性矩；Is为上下翼板对截面形心轴的惯性矩；E、G分别为弹性模量和剪切模量；Q(x)和M(x)分别为任意截面x上梁的剪力和弯矩,u为剪切位移的最大差,v为梁的竖向位移；n和k为瑞斯纳(Reissner)参数。且

假定单元上作用着竖向分布荷载,单元内的剪力在单元上线性分布,剪力滞效应仅改变截面上的正应力分布,而不改变梁截面内力沿纵向的分布,则微分方程(1)的解和它的一阶导数为

(4)

(5)

其中,C1、C2是根据边界条件确定的系数。

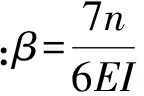
(6a)

(6b)

(6c)

p4=r[s/k-cs1(c-1)]Qi+

(6d)

其中

(7)

将式(6)的次序调整合并,并写成矩阵形式为

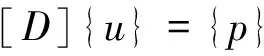
(8)

其中

(9)

(10)

(11)

式中，{u}为剪力滞的广义单元结点位移列阵；{p}为剪力滞的广义单元外荷载向量；[D]为剪力滞的单元系数矩阵。

结构离散,并对各个单元做如上分析后,可按照剪力滞广义平衡与变形协调条件,组集和形成总剪滞系数矩阵和广义荷载列阵。求解得到剪力滞位移列阵,并按以下两式得到各单元的剪力滞系数。

在腹板和翼板的相交处为

(12)

在翼板中点处为

(13)

在得到各单元的剪力滞系数后,由杆系有限元得到的初等梁应力,乘以剪力滞系数,即得考虑剪力滞效应的主梁截面应力分布。

3 主梁应力的监控

基于上述理论,考虑剪滞效应对和平路斜拉桥主梁的应力实施监控,主要做了2个方面的研究：(1)计入剪滞效应的理论应力与实测应力的比较分析;(2)剪滞系数随施工过程的变化规律。以L/4、L/2和3L/4截面为例,如图2所示布置了足够的钢筋应力计测点。

图2 主梁截面钢筋应力计测点布置示意

3.1 计入剪滞效应的理论应力与实测应力比较分析

限于篇幅,仅给出典型截面特定施工状态下的理论应力与实测应力分析比较图,以说明监测结果与研究结论。图3是L/4截面浇筑梁段Z6后的应力比较图,图4是L/2截面浇筑梁段Z28后的应力比较图。

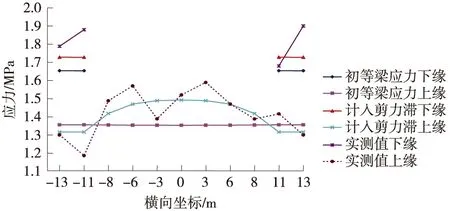
图3 L/4截面浇筑梁段Z6后应力比较

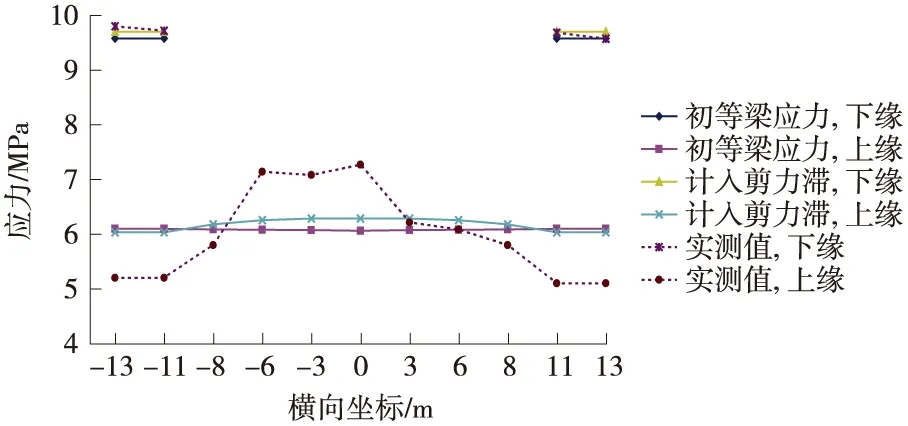
图4 L/2截面浇筑梁段Z28后应力比较

通过全桥各个施工阶段的主梁应力监测比较分析,可得出以下几点结论：

(1)各个截面在相应施工状态下,计入剪滞效应后,实测应力与理论应力更加符合,实测应力值沿截面横向的变化线形与理论值吻合;

(2)当梁段上的截面应力,在该梁段浇筑完成初期,预应力和斜拉索的水平分力较小,横截面的应力状态呈“负剪力滞现象”,随施工推进,斜拉索水平分力的增加使截面轴力增大,截面应力均呈现“正剪力滞现象”;

(3)对图1所示的宽肋距宽翼板主梁而言,正剪力滞效应是有利的。因此,斜拉桥的拉索不但为混凝土主梁提供了免费的体外预应力,而且使主梁的受力状态更加有利。

主梁应力的测试是整个施工过程结构安全预测的主要依据,在实际的施工监控中,对各关键工况下主梁的应力进行实时监测,以判断结构的安全度。图5和图6为Z13梁段截面上的某测点的实测应力与考虑剪滞效应的理论应力在各个施工阶段的比较情况。图7给出了主桥合龙后主梁上、下缘处的理论应力分布情况。

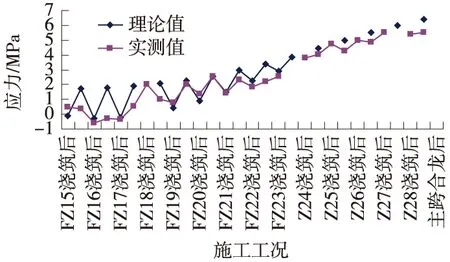
图5 Z13梁段截面上缘实测应力各施工阶段分析

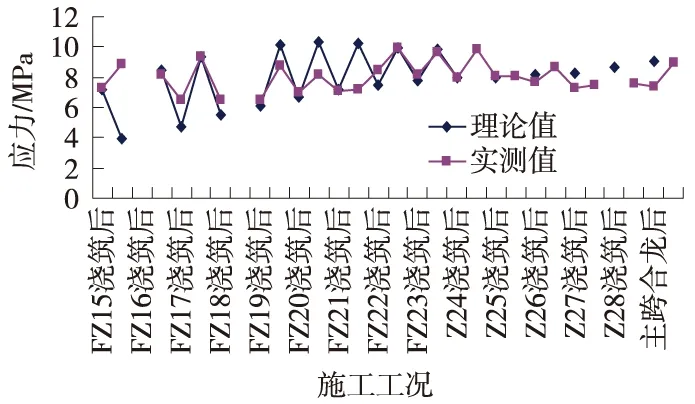
图6 Z13梁段截面下缘实测应力各施工阶段分析

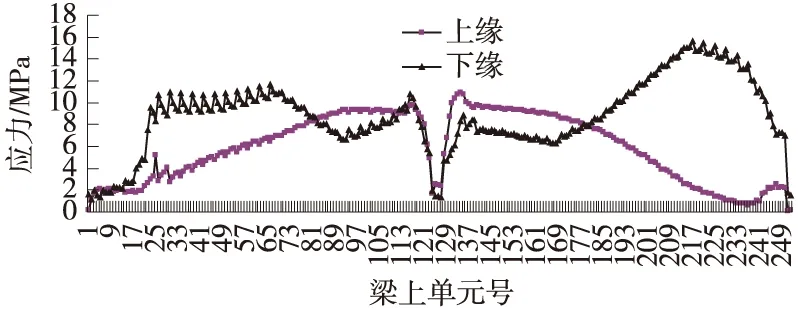
图7 主桥合龙后主梁上、下缘处的应力分布

从图5、图6和图7中可以看出,在施工过程中,主梁的应力基本与理论值符合,主桥合龙后主梁下缘处的最大压应力为15 MPa,上缘处的最大压应力为10 MPa,均处于安全范围之内,成桥应力状态满足设计要求。

3.2 剪滞系数随施工过程的变化规律

对于悬臂施工的PC斜拉桥来说,剪滞效应必定随着施工体系和状态的变化而变化,本文也对指定截面剪滞系数随施工过程的变化进行了详细的分析。仅列出L/2截面和3L/4截面翼板中心的剪滞系数在整个施工过程的变化曲线,见图8和图9。

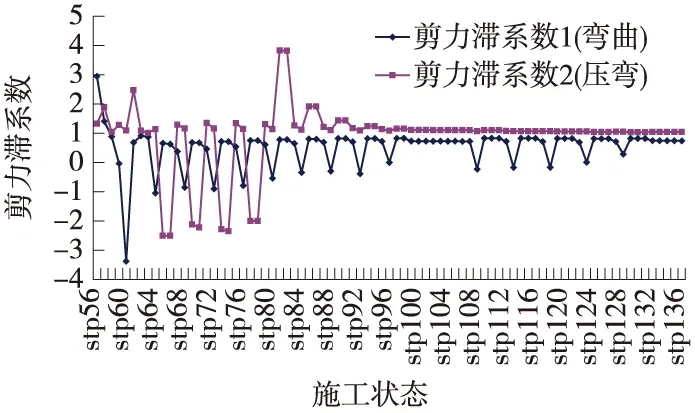
图8 L/2截面翼板中心(z=0)剪滞系数变化

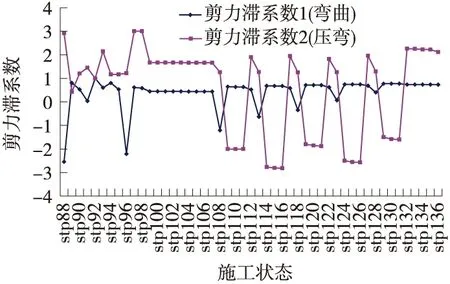
图9 3L/4截面翼板中心(z=0)剪滞系数变化

从剪滞系数变化图可以得知：对于承受轴力和弯曲的斜拉桥主梁来说,弯曲剪滞系数在施工过程中变化幅度较大,而考虑轴力后的压弯剪滞系数在截面受力初期(此时轴力较小)变化较大,而在施工后期(此时截面承受轴力较大),剪滞系数则变得比较稳定。3L/4截面由于轴力相对弯矩比值较小,而压弯剪滞系数变化幅度较大。

4 按有效分布宽度比较

为进一步验证本文的理论与方法的合理性,采用规范[12]进行验证。规范在规定剪滞效应时,并没有对这种宽肋距的双肋式截面做出规定。若按照文献[12]第4.2.2条关于T形截面的规定,显然有效宽度过小,不符合实际。故采用4.2.3条关于箱形截面有效宽度的规定计算,并与本项目所折算的有效宽度进行比较,从而予以验证。

(1)按规范计算的有效宽度

取主梁在悬臂状态下的最大跨度为184 m。则腹板之间的有效宽度

腹板外侧的有效宽度

则按规范确定的顶板有效宽度为

(2)折算有效宽度

在折算有效宽度进行比较时,按照截面内力不变的原则,进行折算,即：顶板实际全宽×顶板计算厚度×初等梁应力=折算有效宽度×顶板计算厚度×计入剪滞后的应力峰值。这里仅列举个别折算有效宽度为：

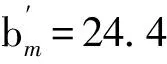
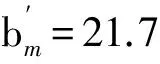
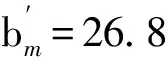
由上比较可以看出,按文献[1,2]所提出的基于能量变分法而导出的有限梁段法考虑剪滞效应,最后折算为有效宽度与按规范计算的有效宽度相比较为接近。且按照规范计算的有效宽度偏小,进行设计是偏于安全的。事实上,基于能量变分法而导出的有限梁段法属于解析解答,更加符合实际情况。

5 结语

(1)按照基于能量变分法而导出的有限梁段法考虑剪滞效应进行主梁的应力监测,更加与实测应力符合,能够准确了解主梁的应力状态,判断结构的安全程度。

(2)从大量应力实测值与理论值的比较图中,可知二者是一致的。且肋板下缘、肋板上缘、顶板中心的理论值与实测值均相差很小,说明本文所阐述的计算理论与方法是正确的。而在翼板中心和腹板之间,理论应力值与实测值偏差在若干施工阶段略大,本文假定截面应力的横向分布呈三次抛物线,因此截面应力沿横向分布的曲线形式有待于进一步探讨。

(3)剪滞系数的变化范围是0.8～1.5,这与已有的研究成果是符合的[9]。但剪滞系数受截面轴力影响较大。随斜拉索水平分力增大,截面轴力增大,剪滞系数逐渐减小,剪滞效应减弱。因此剪滞效应与轴力之间的关系有待于进一步探讨。

(4)按照有效分布宽度的概念比较,可知按照规范计算的有效宽度而进行主梁设计是偏于安全的。

[1] 周世军.箱梁剪力滞效应分析的有限梁段法[J].铁道学报,2007(5)：85-88.

[2] 周世军.箱梁的剪力滞效应分析[J].工程力学,2008(2):204-208.

[3] 郭金琼,房贞政,罗孝登.箱形梁桥剪滞效应分析[J].土木工程学报,1983,16(1):1-13.

[4] 张士铎.箱形薄壁梁剪力滞效应[M].北京：人民交通出版社,1998.

[5] 谢旭,黄剑源.薄壁箱形梁桥约束扭转下翘曲、畸变和剪滞效应的空间分析[J].土木工程学报,1995(8)：3-14.

[6] 罗旗帜.变截面多跨箱梁桥剪滞效应分析[J].中国公路学报,1998,11(3):63-70.

[7] 罗旗帜.薄壁曲箱梁桥剪滞效应分析[J].铁道学报,1999,21(5):88-93.

[8] 张士铎,王文州.桥梁工程结构中的负剪力滞效应[M].北京:人民交通出版社,2004.

[9] 罗旗帜.变截面多跨箱梁桥剪力滞效应分析[J].中国公路学报,1998,11(3):63-70.

[10] 王鲁.预应力混凝土斜拉桥剪力滞效应研究[D].成都：西南交通大学,2005.

[11] 周世军.徐州市和平路预应力混凝土斜拉桥剪力滞效应研究报告[R].兰州：兰州交通大学,2008.

[12] 中华人民共和国交通部.JTGD62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社,2004.