纵向轨枕轨道振动特性数值分析

寸冬冬,曾 京,齐 琳

(1.西南交通大学牵引动力国家重点实验室,成都 610031; 2.青岛捷适铁道技术有限公司,北京 100020)

轨道交通在各个国家的现代化进程中都发挥着重要作用,特别是在城市轨道中,不仅大幅提高了能源利用率,减少了环境污染,更是极大增强了运输能力,缓解了城市交通压力。但是随着人们生活水平的提高,轨道交通所引起的环境振动和噪声也引起了越来越多的关注[1]。这就要求轨道结构必须有减振降噪的功能,除此之外,还特别追求减少轨道系统的维修管理成本,提升维修方便性,以保证交通通畅和安全。

纵向轨枕轨道结构由钢轨、扣件、纵向轨枕梁、枕下弹性材料,以及在无砟道床时还附有凸形或台形、L形支座组成。框架式轨下基础,改变了传统的横向轨枕间隔放置来支承钢轨,改用混凝土纵梁连续支撑和固定钢轨的结构设计,在左右的纵梁之间采用特殊结构的混凝土进行横向刚性连接,组成“框架式”一体化结构[2]。结合结构振动理论,利用数值方法对纵向轨枕轨道的动力学性能进行分析研究,给出纵向轨枕轨道系统的振动模态,并通过对纵向轨枕轨道系统模型施加简谐荷载和随机荷载,对其进行动力学分析,得到结构的振动传递规律。

1 计算模型

纵向轨枕轨道是梯形轨枕轨道的换代产品,其主要减振原理在于通过将具有较大刚度的轨枕纵梁安置于弹性材料上(可视为点支撑弹簧),形成轻量级质量—弹簧系统,由于其独特的结构设计,即在确保轨道结构纵、横向安全稳定的基础上,可以大幅降低垂向支撑刚度,因此可以大大降低振动向基础传递,达到减振降噪的效果[3,4]。

基于其减振理念,考虑纵向轨枕模态受系统约束影响,建立纵向轨枕轨道-桥梁系统模型[5],包括钢轨、扣件、纵向轨枕、减振材料、基础以及桥梁，如图1所示,为考虑完整的约束条件,取一个桥跨24 m的长度,包括了4个纵向轨枕(46 m)。其模型参数如表1所示。

图1 纵向轨枕轨道系统力学模型(单位：m)

表1 纵向轨枕轨道系统模型参数

2 模态分析

纵向轨枕作为一个实用新型的轨枕轨道结构,要了解其动力性能,有必要先对其自身振动特性(结构模态)做一分析。模态分析是系统振动特性的一种表现形式,由模态分析可以得到纵向轨枕在其轨道结构中的各阶固有频率以及对应的振型。本文取不同减振材料刚度进行固有频率的对比分析,考虑轨道结构主要承受垂向作用力的特点,重点将模型的垂向模态提取出来进行分析,其前10阶振动模态频率如表2所示。可以看出：刚度越大结构固有频率越大。

表2 纵向轨枕垂向前10阶振动模态频率 Hz

振型是结构的相对变形,形象地反映了结构所固有的振动形态。由模态分析可知：减振材料刚度取20 MN/m时,前两阶振型为桥梁弯曲振动模态,其振动频率主要与轨枕自身材料、几何性质以及对桥梁的支撑方式(约束)有关。第5阶振型为纵向轨枕的刚体模态(沉浮),其振动频率主要与轨枕自身质量和减振材料刚度有关；第2、4、6、7、8、10阶振型为一桥跨上4个轨枕的整体弯曲振动模态,第9阶振型为单个轨枕的1阶弯曲振动模态,其振动频率主要与轨枕自身刚度、截面属性以及对其采用的约束方式有关。其他工况的振型与此类似,不再赘述。

从表2中可以看出：刚度越大结构固有频率越大。

3 谐响应分析

谐响应分析是确定一个结构在已知频率的正弦(简谐)载荷作用下结构响应(谐响应)的方法。通过谐响应分析可以计算结构在不同频率下的响应,并得到一些响应值(通常是位移)对频率的曲线,从这些曲线上也可以找到“峰值”响应。谐响应分析使设计人员能预测结构的持续动力特性,从而使设计人员能够验证其设计是否能成功地克服共振、疲劳,以及其他受迫振动引起的有害效果。

由结构振动理论,将纵向轨枕轨道系统简化为质量弹簧系统,可知：减小扣件和枕下减振材料刚度可以降低系统的传递系数。又因为一般情况下扣件刚度要远大于枕下减振材料的刚度,所以降低减振材料刚度,会使振动衰减更明显,但是,在考虑减振性能的同时又要注意乘客的乘车舒适性及车辆的运行安全性[6-8]。综合考虑,采用20 MN/m的减振材料刚度,对不同阻尼条件下纵向轨枕轨道系统进行谐响应分析。

谐响应分析只计算结构的稳态受迫振动,发生在激励开始时的瞬态振动不在谐响应分析中考虑。它可以采用3种方法：完全法、缩减法、模态叠加法。通过ANSYS大型有限元软件,利用完全法,在模型的左右轨上同时施加同相位的变频简谐荷载P,表达式如(1)式,其中常荷载P0表示静轮重,简谐荷载幅值Pt表示轮轨作用力的动态部分(取静轮重的0.4倍)。加载位置和响应拾取点如图2所示。

(1)

其中P0=-53 kN,Pt=0.4P0,f取值范围为：0～100 Hz,Δf=1 Hz。

为了了解减振材料阻尼对纵向轨枕轨道结构的影响,分别选取C1=10 kNs/m、C2=25 kNs/m、C3=50 kNs/m三组阻尼参数,进行谐响应计算,得到钢轨、纵向轨枕、桥面的位移响应如图3～图5所示。

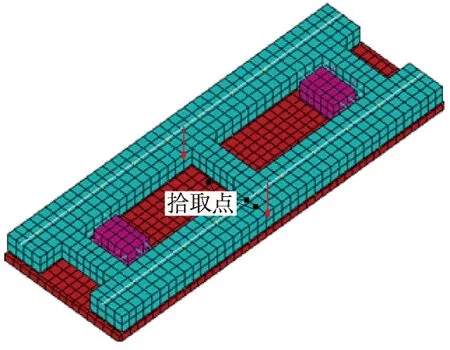
图2 简谐荷载施加方式和拾取点位置

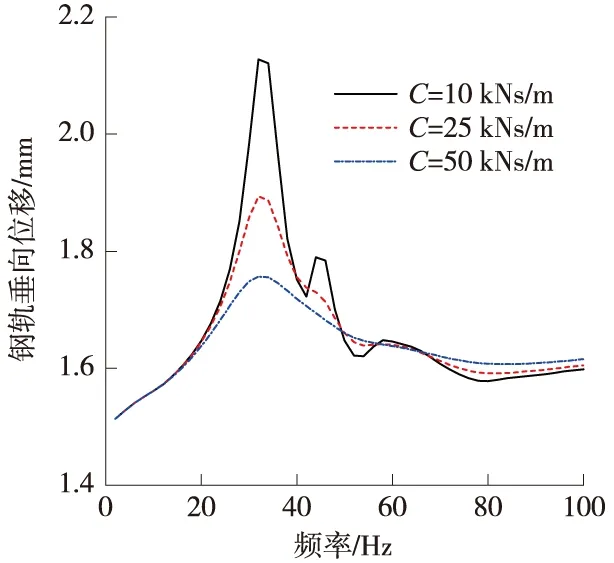
图3 钢轨垂向位移响应

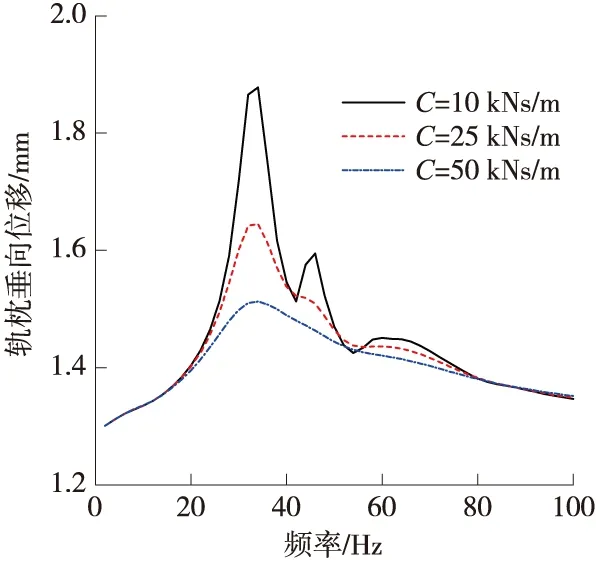
图4 轨枕垂向位移响应

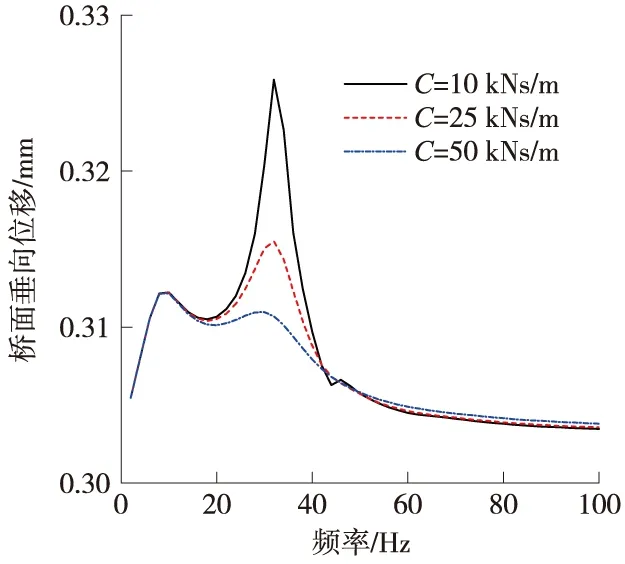
图5 桥面垂向位移响应

在32 Hz和44 Hz左右,轨道结构各部分的垂向位移值都有“峰值”响应,与单个轨枕垂向前两阶固有频率相吻合。在9 Hz附近,桥面板的垂向位移值有“峰值”响应,与桥梁第一阶弯曲固有频率相吻合,说明“峰值”处激振荷载的频率与轨道结构的固有频率相同,结构发生了共振。

对比不同阻尼下纵向轨枕轨道相同位置的垂向位移响应,随着阻尼的增大,轨道结构各部分的“峰值”响应越小。

对比相同阻尼下纵向轨枕轨道不同位置的垂向位移响应,钢轨到纵向轨枕的位移响应变化不大,说明扣件在研究频段内没有起到隔振的效果,而轨枕到桥的位移响应相差近1个数量级,说明枕下减振材料起到了明显的隔振效果。

4 随机响应分析

为了更实际地了解纵向轨枕轨道结构的振动传递规律,采用单轮对的动态轮轨力作为荷载[9](图6),移动施加到有限元模型上,对随机荷载作用下的轨道结构振动响应进行分析。考虑到一般钢轨的振动频率较高,要求模型的荷载时间步长要较小,但过小的时间步长又影响计算速度,所以综合考虑,模型中采用的时间步长为0.5 ms。

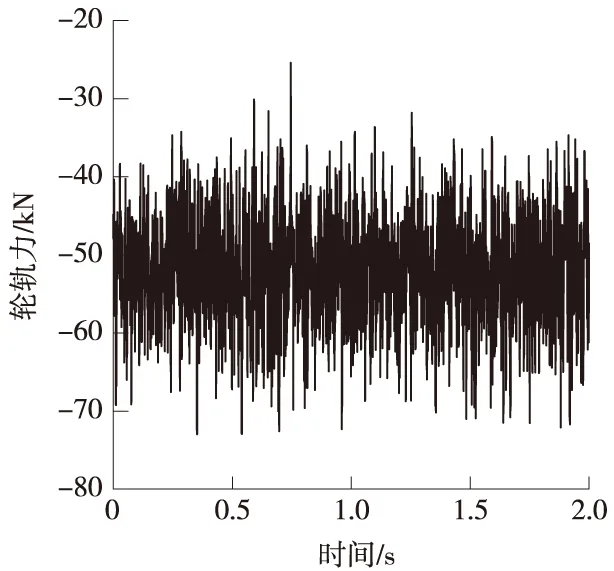
图6 地铁车轮轨力(速度：72 km/h)

模型中减振材料的刚度和阻尼分别取：K=20 MN/m,C=25 kNs/m。与前面谐响应分析相同,拾取第二个轨枕中部对应钢轨、轨枕和桥梁的振动响应值。分析拾取点的振动加速度,绘制其加速度时程图,并对其进行FFT变换,得到加速度的频谱图。如图7所示。

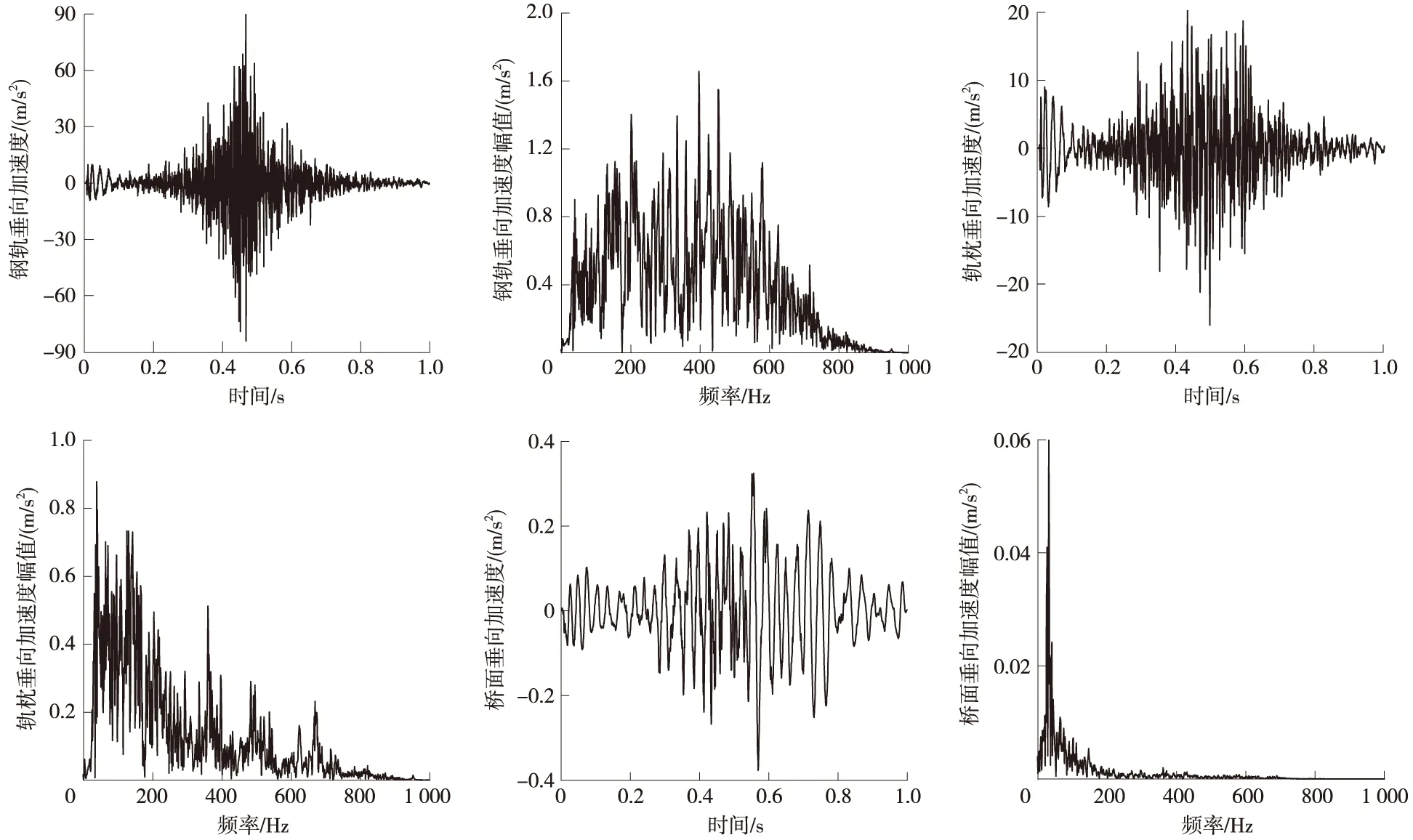
图7 纵向轨枕轨道结构垂向振动加速度时程图与频谱图

钢轨、轨枕以及桥面加速度最大值分别为89.5、19.8、0.32 m/s2。

钢轨加速度幅值频谱很丰富,主要分布在800 Hz以下频段；轨枕加速度幅值主要分布在300 Hz以下,350～410 Hz,490～550 Hz等频段；桥面加速度幅值主要分布在100 Hz以下频段。显然,从钢轨到轨枕再到桥梁,高频成分越来越少；对比而言,轨枕到桥面加速度衰减很多,说明了减振材料对振动衰减的作用明显。

为了直观地说明纵向轨枕轨道结构在随机荷载作用下的振动衰减情况,采用1/3倍频程曲线来描述轨道结构的振动加速度响应,其计算方法是首先对采样信号进行快速傅立叶变换,计算出功率谱或幅值谱,然后用功率谱或幅值谱的数据,计算每一个中心频带的带宽内数据的平均值,然后,根据公式(2)得到每个中心频率处的加速度级[10]。

(2)

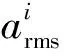
根据以上计算式,可以得到结构的振动加速度如图8所示。

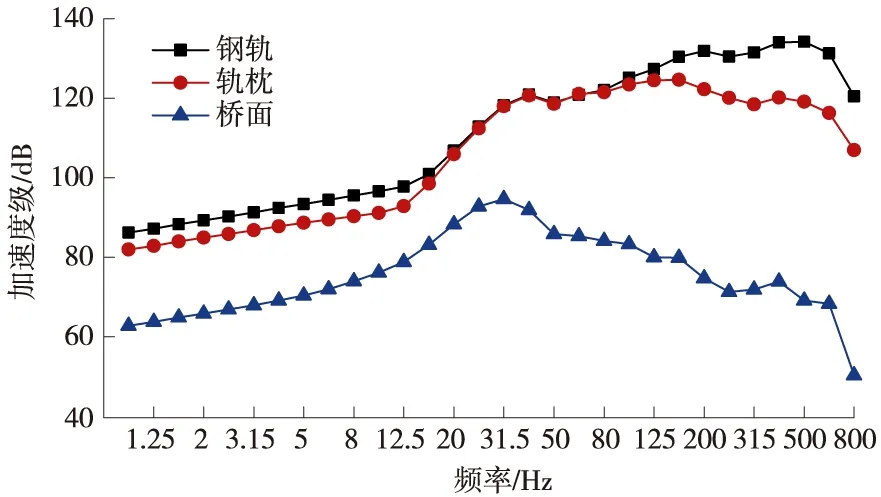
图8 纵向轨枕轨道结构加速度三分之一倍频程曲线

纵向轨枕轨道结构加速度级在31.5 Hz处有峰值,这与前面频谱分析一致,钢轨、轨枕以及桥梁最大加速度级分别为：134.2、124.5 dB和94.6 dB。

钢轨到轨枕的振动加速级变化不大,125 Hz以下,平均减小4～5 dB,125 Hz以上平均减小11 dB左右,说明扣件只对高频振动有衰减作用,而且作用有限；轨枕到桥面的加速度级衰减明显,31.5 Hz以下,平均减小18 dB,31.5 Hz以上平均减小40 dB,可以看出枕下减振材料对研究频段的加速度响应有很好的衰减作用,特别是在31.5 Hz以上的频段,振动衰减明显。

5 结语

(1)建立了纵向轨枕轨道-桥梁耦合模型,通过模态分析提取前10阶的垂向模态。结果显示：减振材料刚度越大,结构固有频率越高；重点分析减振材料取20 MN/m时的结构固有频率及振型。可知：桥梁的一阶弯曲固有频率为8.7 Hz,单个轨枕的浮沉和一阶弯曲固有频率分别为31.26 Hz和43.61 Hz。

(2)通过谐响应分析得出：结构的谐响应(垂向位移)会在9,32 Hz和44 Hz处出现“峰值”现象,这与模

态分析结果相吻合；枕下减振材料的阻尼对谐响应的“峰值”影响很大,阻尼越大,“峰值”越小,但过了“峰值”区之后,阻尼越大,谐响应反而越大。

(3)为了分析纵向轨枕轨道结构的实际轮轨力作用下的随机响应,以单轮对的轮轨力作为移动荷载,对纵向轨枕轨道结构进行了瞬态分析,得出其时域和频域的加速度响应值。时域内,钢轨、轨枕以及桥面加速度最大值分别为89.5、19.8、0.32 m/s2；频域内,相比钢轨,轨枕加速度在400 Hz以上的高频振动明显减小；而相比前两者,桥梁加速度在50 Hz以上的振动几乎可以忽略。

(4)利用1/3倍频程来描述纵向轨枕轨道结构的振动衰减情况,结果显示：扣件只对125 Hz以上的高频振动有衰减作用,减小量约为11 dB,枕下减振材料对31.5 Hz以下的振动衰减较小,约为18 dB,对31.5 Hz以上频域的振动衰减效果显著,约为40 dB。

[1] 孟晓东,顾瑾.地铁振动对周围环境的影响[J].上海铁道科技,2004，12(6):33-34.

[2] 齐琳,等.纵向轨枕和减振轨道系统.中国,201020116820 [P].2010-11-24.

[3] 齐琳,夏禾,任静.梯形轨枕轨道的减振特性分析及论证[J]. 铁道标准设计,2007(10):67-70．

[4] Hiromi Inoue,Yasuo Zenda, L.Qi,andC.Y.Xia. DYNAMIC EXPERIMENT OF AN URBAN ELEVATED BRIDGE WITH LADDER TRACK UNDER MOVING TRAINS[ISEV]. 2009.

[5] 胡国良,等.ANSYS11.0入门与提高[M].北京：国防工业出版社,2009．

[6] 苏宇,刘维宁,孙晓静.梯形轨道减振性能试验研究和数值模拟分析[J].都市快轨交通,2007,6(6):50-54.

[7] 马娜.桥上梯形轨枕轨道动力特性分析[D].成都：西南交通大学,2007.

[8] 北京交通大学.梯形轨枕轨道实验室振动试验报告[R].北京：北京交通大学,2008.

[9] 翟婉明.车辆-轨道耦合动力学[M].3版.北京:中国铁道出版社,2007.

[10] 黄文梅,熊桂林,等.信号分析与处理—MATLAB语言及应用[M].长沙:国防科技大学出版社,2000.