基于振动测量的视宁度测量方法研究*
2012-01-25宋佳阳金振宇程向明
宋佳阳,刘 忠,金振宇,程向明
(1.中国科学院国家天文台/云南天文台,云南 昆明 650011;2.中国科学院研究生院,北京 100049)
由于大气湍流的存在,地面望远镜对天文目标成像时,像质会受到衰减。Kolmogorov对大气湍流的研究,以及Tartarski对湍流介质中光学传播的研究表明,这种像质的衰减本质是折射率起伏对波前的影响[1-2]。Fried在对经过湍流大气后波前畸变、光学分辨率、长曝光和短曝光的传递函数进行研究后,提出了一个全新的参数——大气相干长度r0,描述湍流大气造成的像质衰减程度[3-4]。
视宁度参数r0的测量对天文望远镜的选址起着至关重要的作用,r0的大小是衡量台址优劣的最重要参数之一。随着对光波在大气中传播理论的深入理解以及技术的发展,视宁度参数的测量技术也日渐成熟,出现了各式各样的测量视宁度的设备,目前国际天文界广泛使用的仪器是差分像运动视宁度监测仪,但它比较笨重,携带不方便。在选址初期对台址进行普查时,由于待选地点较多,需要经常携带监测仪器转移观测地。Pickering衍射环法可用口径为5英寸的望远镜测视宁度,但依靠目测,受主观因素的影响,误差大,只在踏勘阶段有一定意义,长焦拖影法存在对星像抖动的高频截止[5]。
为此研究了一种新的用小口径望远镜测量视宁度的方法:采用口径为10 cm左右的便携式望远镜,测量经过大气湍流波前到达角的起伏(即湍流大气造成的单个星像抖动的方差),同时利用加速度传感器测量望远镜本身抖动造成的星像运动方差,并将其从星像运动的方差中扣除,最后根据星像运动方差与视宁度参数r0的关系得到视宁度参数。
目前在口径30 cm的DIMM上进行试验,子瞳直径为7 cm,取单个星像,相当于口径为7 cm的望远镜,并将测得的结果与DIMM作对比。
1 基本原理
对于小口径望远镜,视宁度的影响主要体现在像的随机运动,即波前到达角的起伏。根据Sarazin的计算,从星像运动测出的波前到达角起伏的方差σ2与视宁度r0关系为[6]:

为了使模型简化,在之后的推导和实验中只考虑星像在一个方向上的抖动,在该方向上位移用s表示,速度用v表示,加速度用a表示。根据Kolmogorov湍流理论,大气湍流引起的折射率变化近似为一个遍历过程,因此星像抖动的方差在不同方向是相等的。故上式在一个方向上的表达式为:

只要能求出星像抖动的方差,就能得到视宁度参量r0。但由于望远镜本身的振动和跟踪误差,通过单个星像判定视宁度参量,会引入额外的抖动方差,设为,真正由大气湍流造成的星像抖动方差设为,两者不相关。最终从CCD上测得星像抖动的方差为:

设计一个方案,选用加速度传感器测量望远镜运动的加速度并推算出位移,从而求出望远镜抖动角度的方差。
在镜筒首尾各装一个同样参数的加速度传感器,两加速度传感器的敏感方向一致,相距为l。以靠近CCD一端的加速度传感器为参考点,两加速度传感器较差测量相对加速度Δa,可推算出相对位移Δs的变化,再除以两加速度传感器距离l,即可得到望远镜振动导致镜筒指向角度变化的方差。设v0为初速度,s0为初始位移,a(t)通过加速度传感器测得,v0、s0为未知常数,则位移s(t)为:

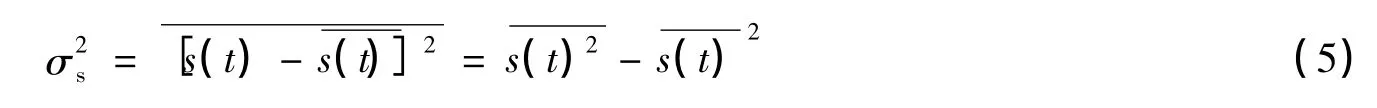
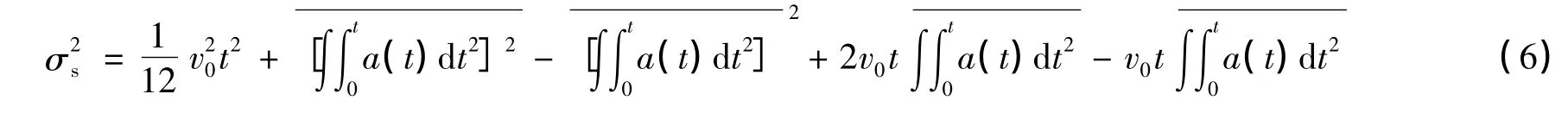
2 加速度传感器测量振动
将望远镜的振动近似为简谐振动,根据DIMM的情况可估计望远镜的抖动振幅,一般在微米量级,设为2μm,频率设为5 Hz,根据简谐振动原理可得加速度幅值为0.002 ms-2。因此选用BZ1189加速度传感器,灵敏度为2000 mA/ms-2,量程为±4 ms-2,是一种压电式加速度传感器。压电式加速度传感器是灵敏度最高的加速度传感器。由于加速度传感器是一种惯性式传感器,是利用弹簧质量系统的强迫振动进行振动测量,所以传感器在相同加速度幅值、不同加速度频率的振动激励下电荷灵敏度的响应不同。在小于1 Hz的低频端,幅值随着频率的降低逐渐衰减,到0.1 Hz时,衰减到-1 dB,对直流量没有响应。这对加速度的测量带来了误差,在低频端反应尤为明显。
振动是物体绕平衡位置(或平均位置)往复运动的一种形式,通常用一些物理参量(如位移、速度、加速度等)随时间变化的函数表征振动的时间历程[7]。在望远镜由风或地面引起的振动中,风或地面给了望远镜激励,望远镜在固有频率附近带有阻尼振动。由跟踪误差引起的望远镜向一个方向的平移,不属于振动,它引起星像中心在图像上的移动反映在星像运动的低频部分或趋势项上。由大气湍流造成的星像抖动不包括直流成分,其频谱大部分功率集中在0.1 Hz以上的部分,且加速度传感器能测量的频率下限为0.1 Hz,故需要对镜筒的位移进行截止频率为0.1 Hz高通滤波,并对星像的运动轨迹进行同样截止频率的高通滤波。望远镜跟踪运动近似于匀速圆周运动,其匀速部分加速度传感器探测不到,圆周运动的加速度与加速度传感器敏感方向垂直,经估算,这样速度的匀速圆周运动产生的加速度在10-9ms-2量级,远低于传感器的灵敏度,不会对测量结果造成影响。(6)式中的v0是指开始测量时,望远镜在振动时的速度,在积分中附加一个v0,对位移s而言,只是加了斜率与v0成正比的一阶趋势项,通过去趋势项可以消除,消除趋势项后的结果和积分时假定v0=0算出的位移方差是一样的。消去v0项后,(6)式可简化为:
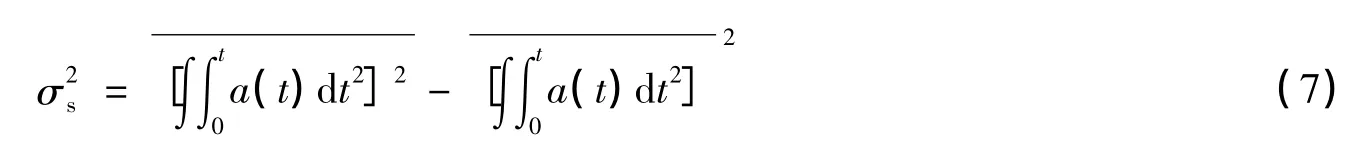
设镜筒口的加速度传感器的物理参数下标为1,靠近CCD的传感器物理参数下标为2,a1(t)与a2(t)分别是其加速度,且相对加速度Δa(t)=a1(t)-a2(t),其相对初始速度为Δv0,相对位移Δs(t)=s1(t)-s2(t),则:

最终要求的是望远镜镜筒振动角度的方差,设α为镜筒偏离平衡位置的角度,即,且:

则望远镜镜筒抖动角度的方差:
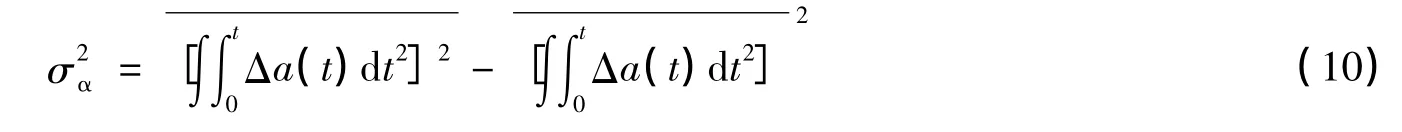
从(10)式可以看出只要测得加速度传感器1与加速度传感器2的加速度,就能得到望远镜抖动角度的方差。
由于积分误差的累积,在对加速度进行二次积分后,得到的位移曲线存在趋势项,使位移曲线远离实际值,这种失真主要体现在位移的低频部分,必须对位移进行高通滤波才能得到可靠的结果。
设计了一套振动产生装置对该传感器进行了测试,可产生在一定频率下振幅约60.5μm的振动,对从加速度积分得到的位移进行高通滤波后,基本上消除了加速度测量误差所产生的趋势项,得到了较为精确的振幅曲线。

图1 安装了加速度传感器的DIMMFig.1 DIMM with the acceleration sensor mounted
3 实测实验
在30 cm口径的DIMM上安装了加速度测量装置,以便与DIMM测得的视宁度数据对比。DIMM子瞳口径为7 cm,焦长303.9 cm。两加速度传感器距离为50.5 cm。将CCD分为x和y两个方向(对应DIMM的横向和纵向),加速度传感器敏感方向与CCD的y方向平行。
DIMM采集程序记录星像在CCD上的坐标,10 s一组,计算一个r0,将星像坐标保存为一个文件并记录采集结束时间保存在文件里。加速度数据由另一台计算机采集,每次采集100 s保存为一个文件,并记录采集结束的时间。采集前两台计算机同步时间,之后再根据星像坐标数据与加速度数据所记录的时间,提取时间上重合的数据段,用来分析计算r0。
为了减小环境电磁波的干扰,加速度信号的采集方式为差分输入,可在一定程度上提高信噪比。所得的信号为靠近镜筒口的加速度传感器信号减去靠近CCD的加速度传感器信号,即(10)式中的Δa。
2011年4月8日北京时间21:00~23:00,在云南天文台进行了观测,得到了一些星像坐标数据与加速度数据。
4 数据处理
由于传感器的敏感方向对应CCD的y方向,所以只分析y方向的星像坐标数据,并利用y方向的星像坐标数据和加速度数据计算视宁度参数r0。视宁度造成的星像抖动的频率主要分布在0.1~50 Hz的范围内,此频范围外的能量很小。尤其是小于0.1 Hz的部分主要是由望远镜的跟踪误差引起的,而且0.1 Hz以下的频率不在加速度传感器的正常工作频率范围内,所以将频率在0.1 Hz以下的星像抖动成分滤除。
根据(7)式,需要两次定积分才能得到位移的方差。第1次积分从加速度到速度,第2次积分从速度到位移,积分方法为梯形积分。由于信号的趋势项不可能完全去除,残余的微小误差在积分过程中将被放大,甚至波形发生畸变[8]。
直接积分得到的位移曲线如图2,直接积分得到的位移远远大于从CCD上体现的对星像抖动的影响。这显然不是由望远镜抖动造成的,主要是因为误差的累积。如果直接以此结果作为望远镜抖动造成的星像位移从单个星像抖动中扣除,那么剩余的值将是负值,无法得到视宁度参数。
测量信号中的趋势项和实际信号的周期比较要长很多,此时可以先把测到的信号进行高通滤波处理,滤除低频趋势项。此种消除趋势项的方法要求必须对所测结构的基频有一个大致了解,在对结构基频了解的基础上,设置一个合适的高通滤波截止频率[9]。因此必须对积分得到的位移进行滤波,才能得到合理的位移曲线。
由于积分对噪声的累积造成整体波形的畸变,主要体现在低频部分。无法准确得到在所有频率范围内的位移信号,只能滤去低频部分,对视宁度造成的单个星像抖动和根据加速度传感器算出望远镜抖动带来星像的抖动进行同样截止频率的高通滤波,去除低频成分,理论上这样会使算出的星像抖动的方差略为减小,而测得的视宁度参数r0比DIMM测得的结果偏大。图3为经截止频率为2.0 Hz的高通滤波后的位移曲线,对比图2可看出趋势项基本消失。

图2 直接积分的位移曲线Fig.2 Displacements resulting from direct integration

图3 经2.0 Hz高通滤波后的位移Fig.3 Displacements resulting from2.0Hz high-frequency bandpass filter
选用两组数据,每组数据含9组视宁度数据,第1组DATA1整体视宁度较好,第2组DATA2整体视宁度较差,对两组数据进行了截止频率为1.0 Hz和2.0 Hz的高通滤波,并将得到的视宁度参数r0与DIMM测得的结果做了比较。根据(2)式与DIMM视宁度计算公式计算视宁度参数,得到的数据见表1和表2。其中差分星像抖动均方根为σd,单个星像抖动均方根σp,利用加速度传感器测得望远镜抖动造成的星像抖动均方根σs,差分像运动法测出的视宁度参数r0(DIMM),直接用单个星像抖动计算出的视宁度参数为(DIRECT),扣除望远镜抖动后的单个星像抖动算出的视宁度参数为(SUBT)。
从表1~2可以看出,进行2.0 Hz的滤波情况比进行1.0 Hz的情况要好一些,相对更接近DIMM测得的结果。积分的噪声累积对算出的位移影响非常大,在这些数据中出现了许多σs>σp的情况,此时无法得到r0值,这种情况不可能由大气湍流造成,在这里主要是由于计算的位移大于实际值,在很大程度上受到积分带来的低频趋势项的影响,而滤波并没有完全消除这种影响,因为这种趋势项在频域具有一定宽度分布,设置一个截止频率进行高通滤波并不能完全滤除。设置较高的截止频率能更好地滤除这种趋势项,但也滤除了更多实际存在的抖动。从表2可以看出,当视宁度相对较差时,用此方法测得的结果相对绝对像运动法明显更接近DIMM测得的结果。在望远镜的抖动比较大时,这种效果相对更明显,在同样的信噪比下,当视宁度较差,即由大气湍流造成的星像抖动方差较大,这种方法得到的结果更接近DIMM。滤波在一定程度上消除了望远镜抖动的影响,但不能完全消除。

表1 根据DATA1得到的r0Table 1 r0from DATA1
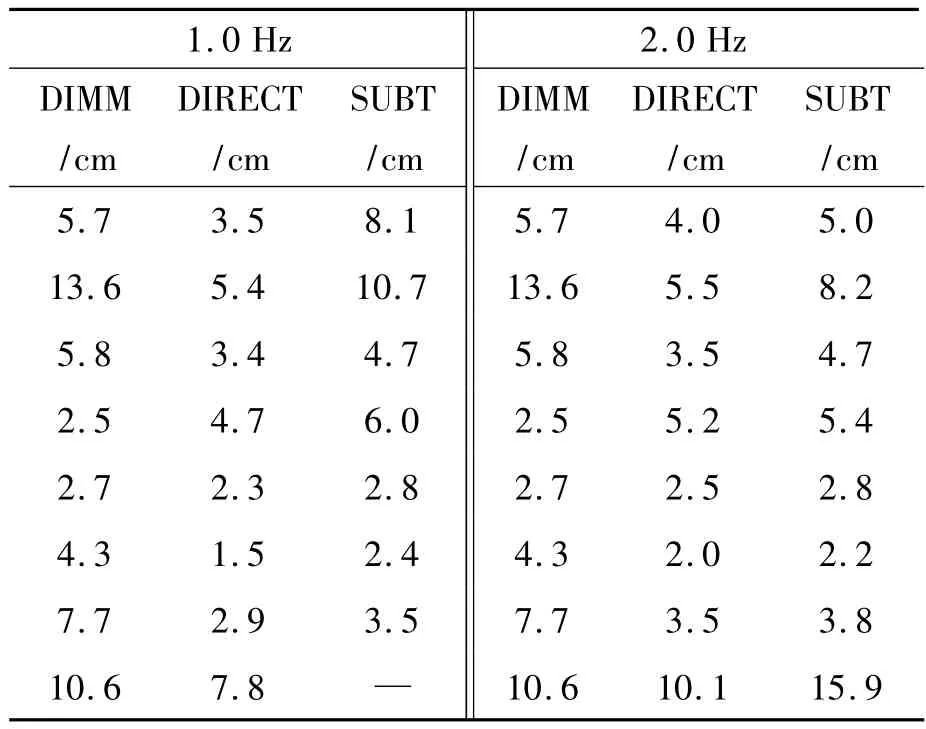
表2 根据DATA2得到的r0Table2 r0from DATA2
5 误差分析
测得的视宁度参数与DIMM测得的视宁度参数相比存在一定误差,经分析误差来源如下:
(1)理论误差:按照此方法在同样的σs下(对位移的测量在一定误差范围内),当σd取不同的值时,得到的r0如图4。
可以看出当DIMM的星像相对抖动的均方根σd越小,即视宁度越好的情况下,误差越大。
当测得的加速度数据存在误差时,该方法在理论上引入了较大的误差。当得到的视宁度误差过大时,视宁度数据已不可用。加速度误差越大,在较小的实际r0条件下,理论上已得不到有效视宁度参数;在加速度误差较小时,在较大的实际r0条件下,理论上得不到有效视宁度。所以减小加速度测量误差可提高视宁度参数的可测量范围。
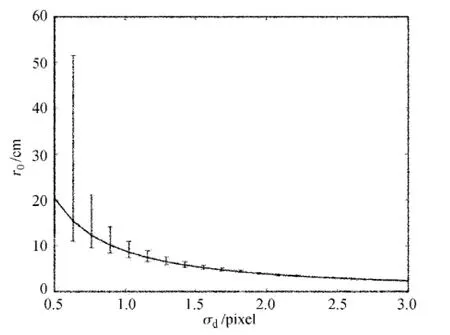
图4 理论误差Fig.4 Theoretical errors of r0
(2)加速度误差与积分误差:由于加速度传感器的幅值频率响应特性,尤其对靠近其可测频率下限的低频端有较大误差,经二次积分产生了低频趋势项。在对位移进行高通滤波时,并没有完全滤除这些趋势项的影响,在不同的时间段内,误差造成的趋势项在频域并不相同,采用同样的截止频率滤波会使测得的视宁度与实际相比有较大差距。
6 结论
用单个星像的运动再扣除由望远镜振动带来的星像抖动测视宁度,可只用单个光瞳,使用口径为10 cm(实验中DIMM的子瞳口径为7 cm)左右的望远镜,相对DIMM便携性好。从最终得到的视宁度数据与DIMM的结果和绝对像运动法得到的结果相比较,可看出该方案在一定程度消除了望远镜抖动对测量视宁度的影响。但由于积分误差的累积,并且滤波并没有完全消除其影响,导致测得的r0与DIMM相比存在较大误差。
[1]V I Tatarski.Wave propagation in a turbulent medium [M].New York:Dover Publication,1961.
[2]V I Tatarski.The effects of the turbulent atmosphere on wave propagation [M].National Science Foundation Report TT-68-50464,1968.
[3]D L Fried.Statistics of a geometric representation of wavefront distortion [J].Journal of the Optical Society of America,1965,55(11):1427-1431.
[4]D L Fried.Limiting resolution looking down through the atmosphere [J].Journal of the Optical Society of America,1966,56(10):1380-1384.
[5]宋正方.星像抖动的时域频谱 [J].天体物理学报,1995,15(3):275-281.Song Zhengfang.The temporal-frequency spectrum of stellar image motion [J].Acta Astrophysica Sinica,1995,15(3):275-281.
[6]Sarazin M,Roddier F.The ESO differential image motion monitor [J].Astronomy and Astrophysics,1990,227(1):294-300.
[7]胡志强,法庆衍,洪宝林,等.随机振动试验应用技术 [M].北京:中国计量出版社,1996.
[8]李强,王太勇,胥永刚.基于频域积分的振动参量转换修正算法 [J].组合机床与自动化加工技术,2005(9):60-61,65.Li Qiang,Wang Taiyong,Xu Yonggang.The modification of the vibration parameter transform based on frequency domain integration[J].Modular Mechine Tool& Automatic Menufacturing Technique,2005(9):60-61,65.
[9]张永强,宋健江,图良尧,等.软件数值积分误差原因分析及改进办法 [J].机械强度,2006,28(3):419-423.Zhang Yongqiang,Song Jianjiang,Tu liangrao,et al.Error analysis and improvement method when numerical integration with software [J].Journal of Mechanical Strength,2006,28(3):419 -423.
