基于在线轨迹规划的混合再入制导方法

王俊波，曲 鑫，任 章

(北京航空航天大学飞行器控制一体化技术实验室，北京100191)

0 Introduction

The reentry guidance problems for reentry vehicles focus mainly on the design of guidance strategies，which satisfy both terminal and path constraints．The conventional reentry guidance technologies can be classified into two main categories:reference trajectory-based guidance(RTG)methods［1－5］and online predictive guidance(OPG)［6－7］methods．RTG methods involve off-line planning of reference trajectory which satisfies both terminal and path constraints and online tracking of this trajectory．Since the reference trajectory of the RTG methods requires extensive preflight analysis，it lacks the adaptability to accommodate unforeseen circumstances during reentry flight．With the development in onboard computational capability，OPG and rapid trajectory planning［8－9］methods have received increasing attention．The OPG methods use online prediction solution to attain control variables and have strong anti-interference ability．In Ref．［6－7］，iterative predictor-corrector method is adopted to meet the required conditions at Terminal Area Energy Management(TAEM)interface．Ref．［8］presented an efficient methodology for faster design of 3 degree of freedom reentry trajectories，which are subjected to all constraints．Ref．［9］have developed the methodology in Ref．［8］with improved quasi equilibrium glide condition(QEGC)．In Ref．［10］，the hybrid entry guidance is described in which the drag-based tracking guidance technology and the numerical predictorcorrector technology are combined together．Most of predictor-corrector algorithms compute complete reentry trajectory onboard by numerically integrating the equations of motion from the current state to required final condition in each predictive guidance cycle and iterative operations are adopted when computing the correct commands．Since massive iterations and integral calculation，the real-time capability of OPG methods has been challenged and the risk of solution nonconvergence in the iteration process is inherent．

A hybrid reentry guidance algorithm for reentry vehicles is presented in this paper，which involve online trajectory planning based on waypoints and trajectory tracking guidance algorithm．The waypoints based on the initial reference trajectory can be used to piecewise implement trajectory planning and the linear quadratic regulator(LQR)controller is adopted to track the re-planning trajectory．The proposed algorithm reduces the calculation time of OPG methods and improves adaptability of RTG methods．

1 Trajectory dynamics

When the earth’s rotation is considered，the dimensionless equations of motion for reentry vehicles are defined as follow:

where r is the radial distance from the earth center to the vehicle，which is normalized by the radius of the earth r0=6378km;V is the earth-relative velocity，which is normalized by;τis the time，which is normalized byλandφare the geographical longitude and latitude，respectively;ωis angular rate of the earth rotation，which is normalized byγis the flight path angle;ψis the heading angle;σis the bank angle;L and D are the dimensionless aerodynamic lift and drag acceleration in the unit of g0，respectively．

Eq．(1)is established in the equatorial coordinate frame(ECF)．In order to help clarify the reentry guidance problem，λandφare converted asandin new coordinate frame respectively．This new coordinate frame，referred to as the guidance coordinate frame(GCF)，allows us to interpretedas the downrange angle andas the crossrange angel．The ECF and GCF are shown in Fig．1．

In Fig．1，OE－XEYEZEis the ECF;o－xyz is the launch coordinate frame;A0is direction angle，i．e．the angle between the ox in o－xyz and the direction of true north，which is positive along clockwise rotation;OE－is the GCF．

Fig．1 shows that OE－XEYEZEis rotated such that the plane given by=0 contains both the initial and final reentry positions and＞0．The relationships between theλ，φandare as follow:

Fig．1 The correlative coordinate frames

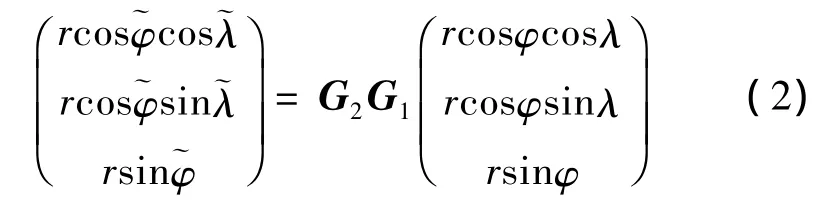
where G1is the conversion matrix between the OEXEYEZEand o－xyz，which can be computed as follow

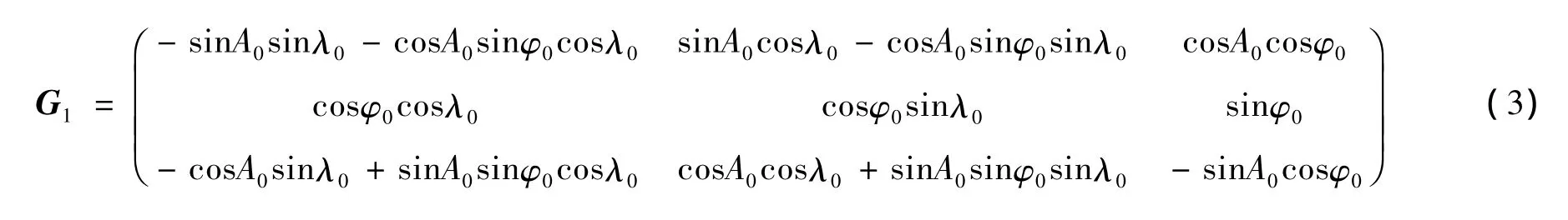
whereλ0andφ0are the geographical longitude and latitude in reentry point．G2is the conversion matrix between the o－xyz and，which can be computed as follow:

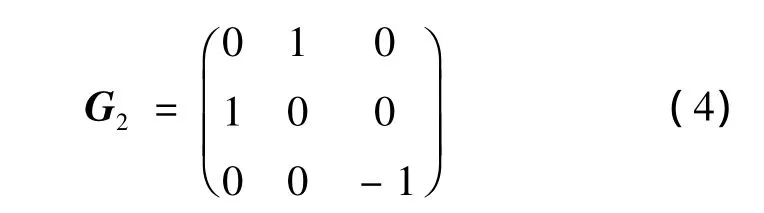
G is defined as follow:

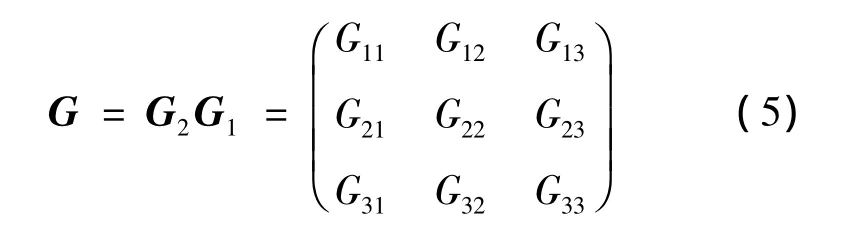
According to the Eq．(2)and Eq．(5)，The~λ andcan be achieved using the following functions:

2 Reentry constraints and way points

2．1 Reentry constraints

The objective of reentry guidance is to effectively control the reentry vehicle from the initial location to the designated location without violating any reentry constraints．The reentry constraints consist of two parts:the path constraints and the terminal constraints．The path constraints contain the heating rate，normal load factor nLand dynamic pressure q．These constrains are expressed as follows［8］:

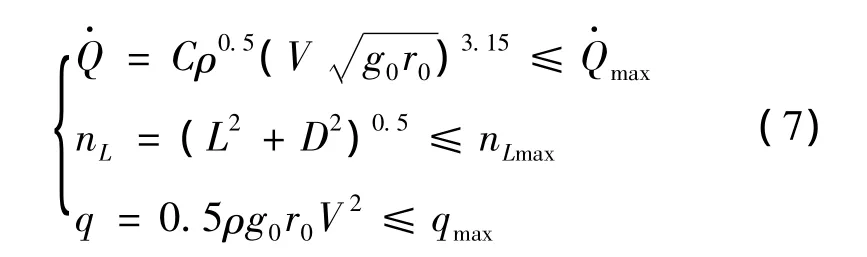
where C is a constant for the computation of heat rate．

To insure the constrains expressed in Eq．(7)are strictly satisfied in the reentry flight，the reentry corridor is established based on V vs h profile．From the reentry corridor，the path constraints are converted to the limits of the controls by the QEGC(seen Ref．7)．From the guidance perspective，αandσare treated as controls．In this paper，theαprofile be assumed as a piecewise linear function of V and theσis used as the only trajectory control．The limits ofσrelate to the path constraints are defined asσmaxandσmin(whichσmax＞σmin≥0)．Interrelated solution procedure can be found in Ref．7．In the guidance process，as long as the bank angle magnitude is betweenσmaxandσmin，the trajectory of reentry vehicle can be ensured in the reentry corridor without violating any physical constraints．

The terminal constraints for reentry guidance problem are expressed as follows:

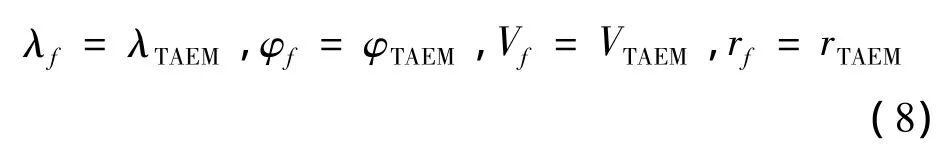
whereλf，φf，Vfand rfare the terminal longitude，latitude，velocity and attitude，respectively;λTAEM，φTAEM，VTAEMand rTAEMare the desired value at TAEM interface．

The energy parameter e is introduced as follow:

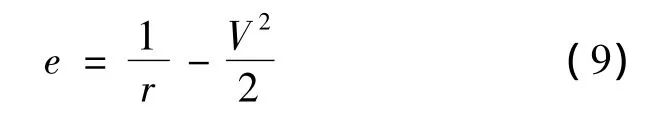
According to Eq．(9)and GCF，The constraints in Eq．(8)are converted to as follow:

where eTAEMis the terminal energy parameter．

2．2 The design of waypoints

The main difference of the working principle between the designed algorithm in this paper and others［8－10］is that the online planning of the reentry trajectory is piecewise implemented by waypoints to reduce the calculation time．In reentry flight，the reentry vehicle should be guided to fly through each waypoint with the appointed flying states(contain position，velocity and attitude)．To obtain appointed flying states of the waypoints，it is necessary to design the initial reference trajectory．

In this paper，the bank angle magnitude of the initial reference trajectory are determined as the piecewise linear function of e．According to initial and terminal V，r，the initial energy parameter e1and eTAEMcan be achieved．The total interval［e1，eTAEM］is divided into n－1 sub-intervals using n way points(the number of n determined according to the time requirement of online trajectory planning):［e1，e2，…，en－1，en］．enis equal to eTAEM．In each subinterval，theσcsatisfies the following formula:

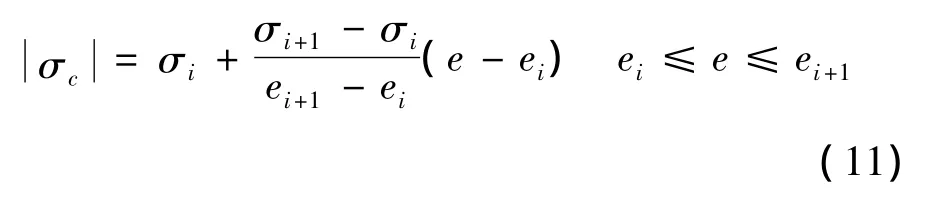
whereσiandσi+1satisfyingσmin≤ σi，σi+1≤σmaxare model parameters．The initial values of［σ1，σ2，…，σn－1，σn］which guide the vehicle to the required downrange without any interference are offline determined by some optimization methods．The sign of bank angle is determined by the lateral logic，which will be discussed in the next section．With the magnitude and sign of the bank angle specified，the Eq(1)is numerically integrated from e1to enand the information of each waypoint can be achieved．Assuming xiand xi+1are the flight parameters of the ith and(i+1)－th way point，respectively，which expressions are as follows:

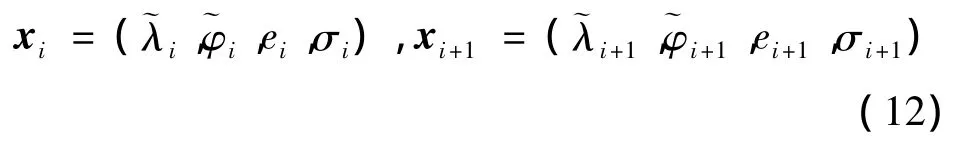
In the reentry flight，the information of each waypoint are stored beforehand in airborne computer to as desired conditions of the piecewise online trajectory planning．

3 Online trajectory planning based on waypoints

Since the presence of dispersion and uncertainties in reentry flight，the reentry trajectory needs to online re-planning based on the initial reentry trajectory．Comparing the conventional trajectory planning from the current condition to TAEM，it only be operated from the current point xnowto next way point．

In the reentry flight，the energy parameter enowof xnowcan be achieved according to V and r measured．The sub-interval［ei，ei+1］(which satisfying ei≤enow≤ei+1)corresponding to enowand the waypoints xiand xi+1can be determined．

The online trajectory planning problem can be simplified to adjustσiandσi+1to deliver the vehicle from xnowto xi+1and the final condition corresponding to ei+1are satisfied as follows:

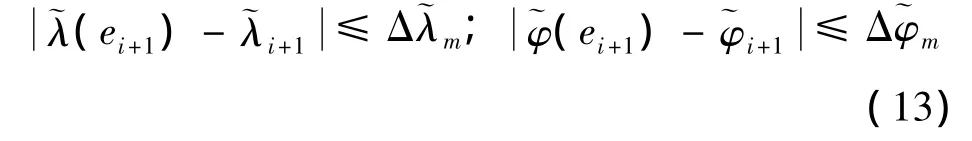
3．1 Longitudinal trajectory planning

The online trajectory planning based on waypoints consists of longitudinal and lateral channel．The longitudinal channel is used to adjustσiandσi+1of instantaneous sub-interval so thatandare equal to the required value．The deviation informationandare as follow:

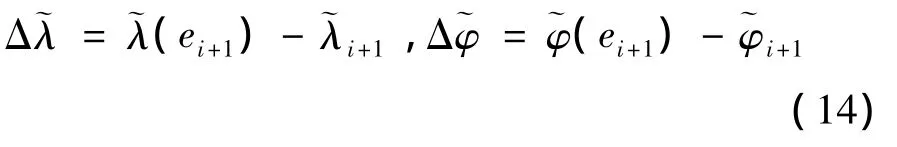
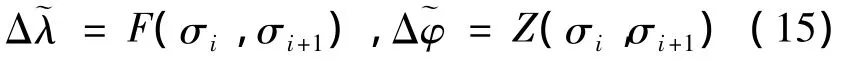
The Eq．(15)is implemented taylor expansion ignoring higher order terms as follows:

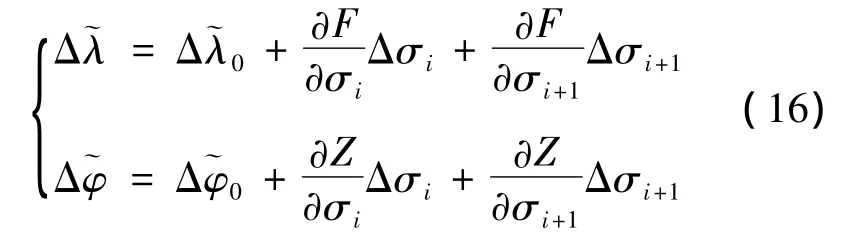
The algorithm procedure is given as follows:

(1)Determine the current momentτi，enowand the way points xiand xi+1;

(2)Implement the numerically integral in［enow，ei+1］，thenandcorresponding to ei+1are obtained．Exit ifandless than the error tolerance，otherwise go to next step;

(3)Perform perturbed trajectory prediction twice to solve∂F/∂σi，∂F/∂σi+1，∂Z/∂σiand∂Z/∂σi+1，thenΔσiandΔσi+1can be attained;

(4)Update the current bank model parameters as follows:

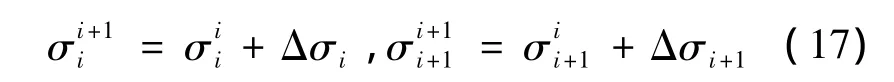
where satisfiedσmin≤≤σmax;

(5)Exit if the deviation less than the error tolerance，otherwise go to step(2)．

3．2 Lateral logic

The task of lateral guidance is determined the sign of the bank angle．The lateral logic is defined as follow:

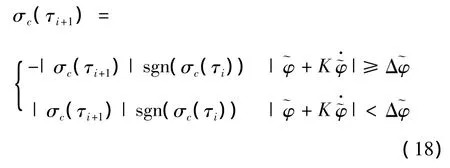
4 Hybrid reentry guidance algorithm

The hybrid reentry guidance algorithm consists two parallel modules．One is the reentry trajectory online planning module which is discussed in abovementioned section．The other is trajectory tracking guidance module．The tracking guidance module is used to real-time track the re-planning reference trajectory by LQR controller．The state variable of LQR controller is given as follow:

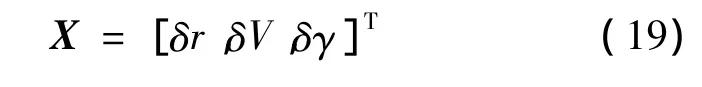
whereδr，δV，δγare disturbance terms．The designed procedure of LQR controller is given in Ref．9．

The hybrid reentry guidance algorithm diagram is shown in Fig 3．

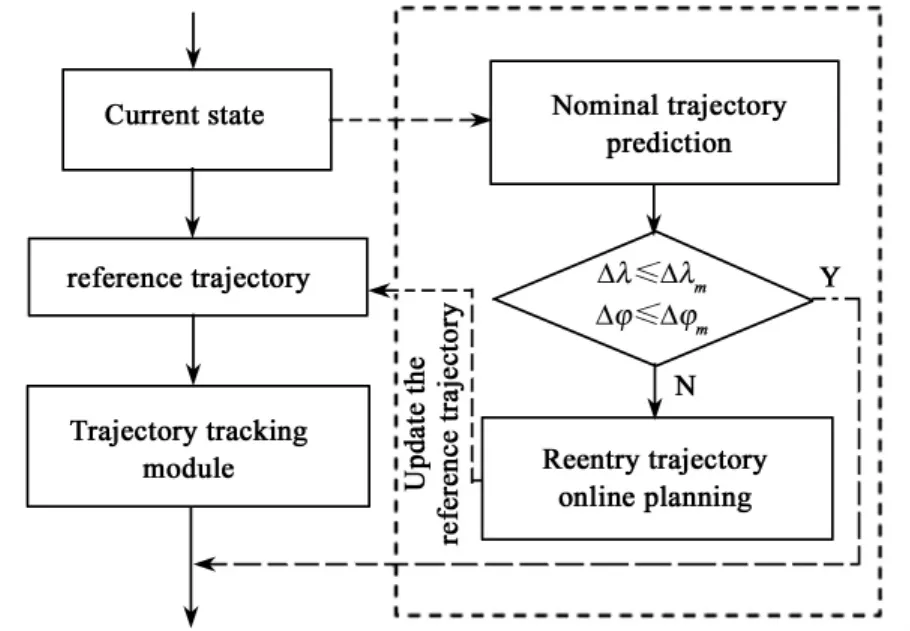
Fig．2 Hybrid reentry guidance algorithm diagram

5 Simulation and analysis

Simulations of the reentry vehicle are used to evaluate the performance of the hybrid reentry guidance algorithm．There are three nominal test cases．The initial and TAEM interface conditions of the three cases are shown in Table1．

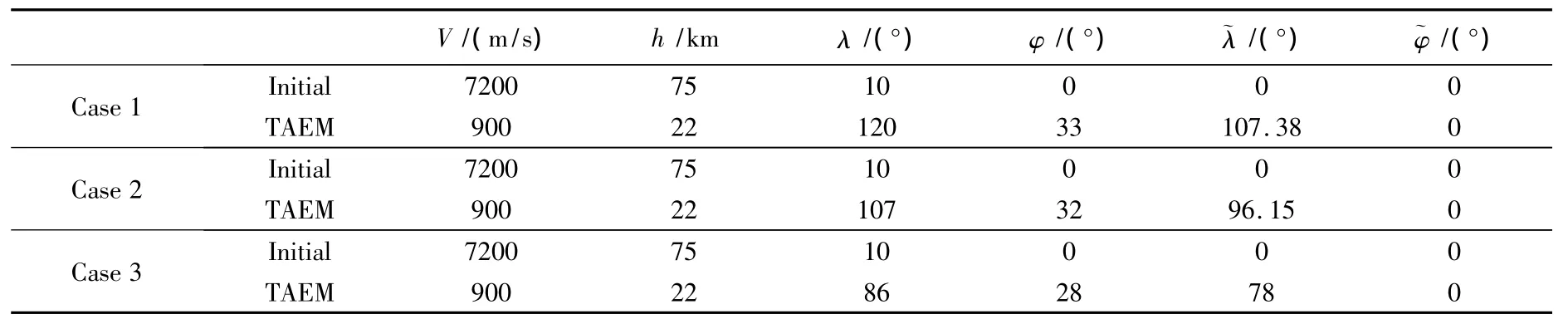
Table 1 The initial and TAEM interface conditions

The acceptable tolerances of TAEM interface are:ΔV＜100m/s，Δh＜2km，＜0．4，＜0．1;The corresponding area of energy parameter is:［e1，eTAEM］，e1=0．5746，eTAEM=0．9901;The path constraints are:nmax=4g，=544．3kW/m2，qmax=26280N/m2;The number of n:n=10．Fig．3 shows the bank angle magnitude of three reference trajectories varied with e．Fig．4 shows the reference trajectories of all cases in the V－h space where the boundaries of path constraints are visible．Fig．5 shows the reference bank angle curve of all cases．Fig．6 shows the longitude-latitude curves of all cases in ECF and GCF，respectively．

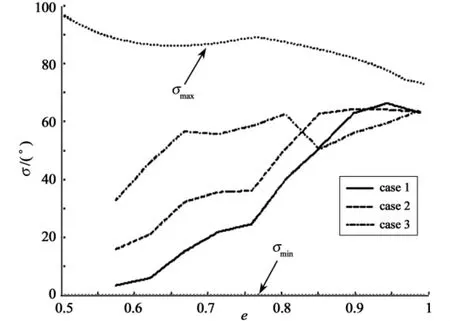
Fig．3 of three reference trajectories

To further test the guidance performance and robustness of the hybrid reentry guidance algorithm under random dispersions encountered in reentry flight，Monte Carlo simulations are conducted．The initial conditions，aerodynamic coefficients(AC)，atmosphere

Fig．4 Reentry trajectories in V vs h space

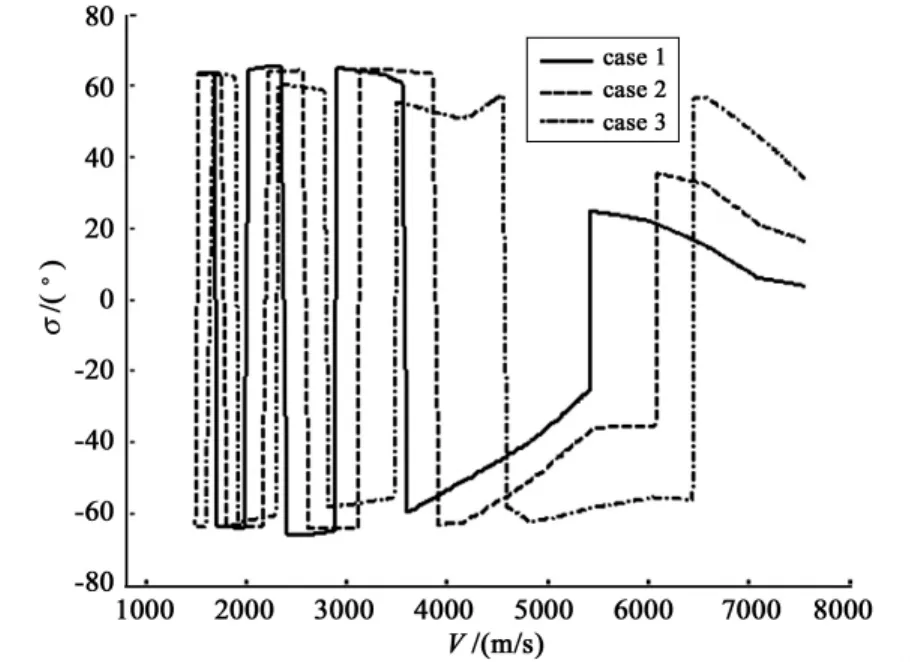
Fig．5 The reference bank angle curves

densityρand vehicle mass m are all dispersed．The dispersions and their standard deviation for Gaussian distribution are given in Table 2．

The dispersion simulation results are presented here for three cases．Fig．7 shows the 300 trajectories of all cases in the V－h space．Fig．8 shows the longitude-latitude errors of the GCF at the TAEM interface along 300 dispersed trajectories．Fig．9 gives the bank angle histories for these 300 dispersed trajectories．Fig．10 shows the velocity and height errors for these 300 dispersed trajectories．

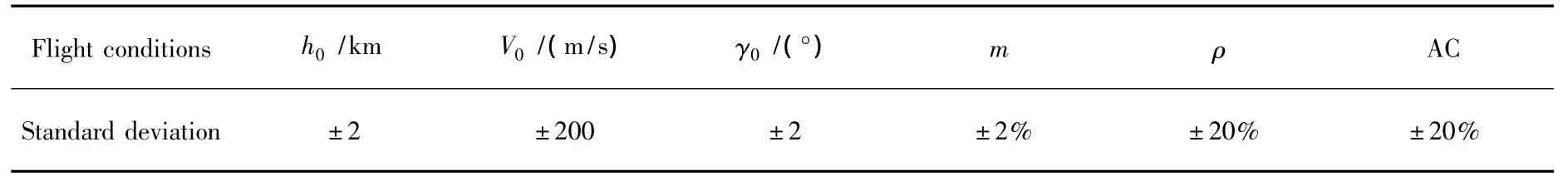
Table 2 Statistics dispersions used in Monte Carlo simulations

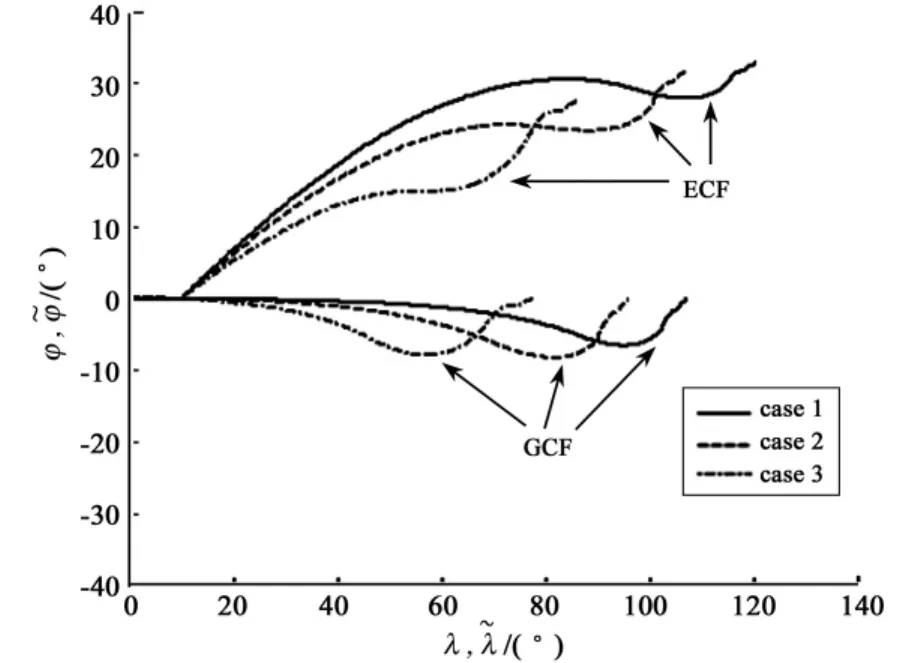
Fig．6 The longitude-latitude curves of all cases

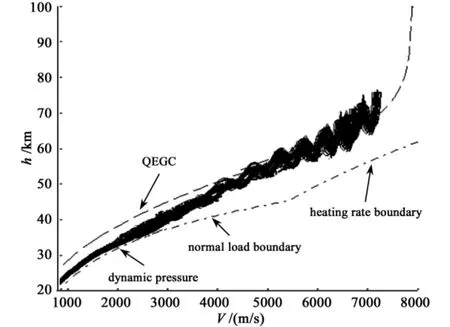
Fig．7 300 dispersed reentry trajectories in V vs h space

Fig．4 and Fig．7 show that all the reentry trajectories are kept in the reentry corridor which means the observance of the path constraints．Fig．8 shows a circle around the zero-deviation．The tolerable error radiuses of the longitude-latitude are 0．4 and 0．1，respectively．The endpoints of almost all of the trajectories lie within error radius．Fig．10 shows that the velocity and attitude errors(relative to the TAME interface)are smaller than the acceptable tolerance of TAEM interface．The average calculating time of each trajectories planning is less than 0．2 seconds in C program on a PC platform with a 2．4GHZ processor．

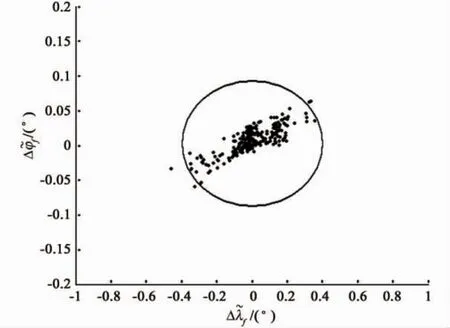
Fig．8 Longitude-latitude errors for 300 dispersed trajectories

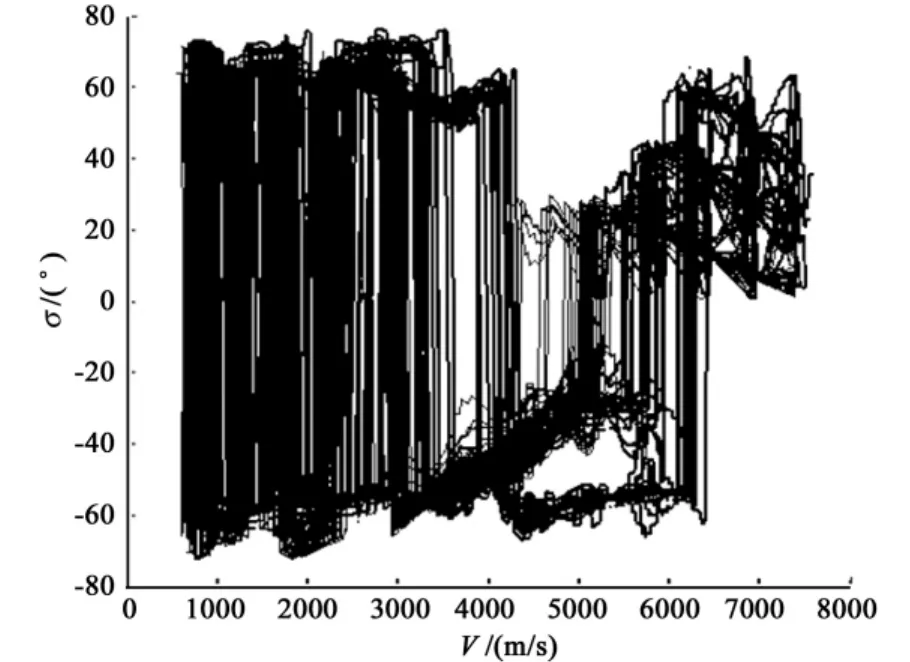
Fig．9 Bank angle histories for 300 dispersed trajectories

6 Conclusion

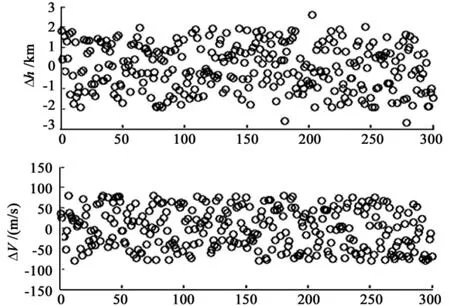
Fig．10 Velocity and height errors for 300 dispersed trajectories

The hybrid reentry guidance algorithm which consists the online trajectory planning based on waypoints and trajectory tracking guidance algorithm is presented for reentry vehicles．The longitude-latitude expressions in GCF are established to help clarify the reentry guidance problem and the initial reference trajectory is generated beforehand to supply information of the waypoints．Finally，the online trajectory planning algorithm based on waypoints and the design of LQR controller are given．Simulation and experimental results indicate that the hybrid reentry guidance algorithm has small errors with respect to the conditions of TAEM interface and preferably real-time ability．

［1］Harpold JC，Graves CA．Shuttle entry guidance［J］．Journal of the Astronautical Sciences，1979，27(3):239－268．

［2］Harpold JC，Gavert D E．Space shuttle entry guidance performance results［J］．Journal of Guidance and Control，1983，6(6):442－447．

［3］Roenneke，Axel J，Stuttgart，et al．Reentry control to a drag-vsenergy profile［J］．Journal of Guidance，Control，and Dynamics，1994，17(5):916－920．

［4］Mease K D，Chen D T，Teufel P，et al．Reduced-order entry trajectory planning for acceleration guidance［J］．Journal of Guidance，Control and Dynamics，2002，25(2):257－266．

［5］Saraf A，Leavitt JA，Chen D T，et al．Design and evaluation of an acceleration guidance algorithm for entry［J］．Journal of Spacecraft and Rockets，2004，41(6):986－996．

［6］Joshi A，Sivan K，Amma S S．Predictor-corrector reentry guidance algorithm with path constraints for atmospheric entry vehicles［J］．Journal of Guidance，Control and Dynamics，2007，30(5):1307－1318．

［7］Xue S B，Lu P．Constrained predictor-corrector entry guidance［J］．Journal of Guidance，Control and Dynamics，2010，33(4):1273－1281．

［8］Shen Z，Lu P．Onboard generation of three-dimensional constrained entrt trajectories［J］．Journal of Guidance，Control and Dynamics，2003，26(1):110－121．

［9］Yong E M，Tang G J，Chen L．Rapid trajectory planning for hypersonic unpowered long-range reentry vehicles with multiconstrains［J］．Journal of Astronautics，2008，29(1):46－52．

［10］Hu JX，Chen K J，Zhao H Y，et al．Hybrid entry guidance for reusable launch vehicles［J］．Journal of Astronautics，2007，28(1):213－217．