分形几何在自然科学中的应用

徐沥泉

教授，无锡市教育研究中心，江苏 无锡 214001

本文综述了分形几何在物理学、生物学、工程技术、生命科学、地震学等领域的应用。从中我们还可以发现大千世界中数学的优美。

分形理论在自然界与社会活动中得到了广泛应用。在自然科学的各个研究领域里，人们自觉地运用分形几何学，从数理化、天地生到工农医等领域都获得了许多新认识和新进展。如物理学中的湍流（流体的不规则运动）与相变（物体由一种相态到另一种相态的转变）；化学中的高分子链、多相催化剂表面特征、凝胶（溶胶或溶液中的胶体粒子或高分子形成的空间网状结构）；天文学中的星团分布、宇宙大尺度结构的形成；地学中的渗流（流体在多孔介质中的流动），分形地貌、河流与水系；生物学中的全息现象；医学中的人体组织结构，如血管、肺、心脏等的分形描述；材料的损伤断裂……无不显示出分形理论和方法的威力［1］。

1 在物理学和工程技术中的应用

分形理论自产生之日起就得到了物理学家的高度重视，并在物理学中得到广泛应用。其原因是分形几何结构代表了自然界中普遍存在的更加接近于自然的物质结构，它具有巨大的实用上的重要性；另一方面是因为自然界中存在着两种基本对称性即平移对称性和扩展对称性，对后者而言人们不甚清楚。近20年来，分形理论被推广应用到若干远离平衡态的不可逆生长过程中，这些过程显示了自相似的扩展对称性。分形物理所研究的内容主要包括分形结构晶格（原子在晶体中排列规律的空间格架叫做晶格）或物质中的力、热、光、电性能，另一是研究若干属于随机分形的具有统计自相似或自仿射意义的物理现象。如分形凝聚，分形动力学，分形中的相变，材料科学中的分形，物理中的多重分形。图1和图2是文［2］和文［3］给出的电解实验和热对流中的多重分形的模拟形体图。十分有趣的是，图1—2揭示了热对流在黄金分割点的扰动和临界圆周映射具有相同的多重分形结构。

图1 电解实验形体图

图2 热对流形体图

分形理论在机械工程及自动化中得以广泛应用，如核动力工程、冶金、化工和制冷等工业中沸腾换热的分形分析。近年来，随着纳米流体这一新领域的出现，使沸腾换热情况变得复杂化。对此，传统经典模型已经束手无策。一些经典理论与公式不能充分揭示沸腾换热的物理机理。比如，对于活化密度，从实验得出的经验公式为［3］

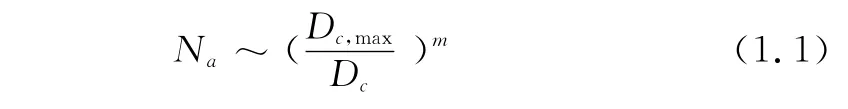
其中，Dc，max，Dc分别为加热面上最大活化穴直径和活化穴直径，Na为加热壁面上的活化核心密度，m（＝0.65）为经验常数，这个经验常数所隐藏的物理本质并不清楚。为了进一步揭示那些隐含在这些经验常数背后的更深层次的物理机理，深刻解释沸腾换热现象和机理。分形几何理论与方法可能给我们提供一种新的思路和方法，详见文［4］。

分形天线工程又是分形与电动力学相结合的一个重要应用。文［5］介绍了分形天线工程的产生背景和发展、研究领域与方法。分形天线工程主要分为分形单元研究和分形阵列研究。分形单元研究主要集中在小型化和多频特性方面；分形阵列研究主要集中于快速波束成形算法、低旁瓣和宽带宽角扫描等方面的研究。同时，分形还和天线研究领域的其他成果相结合，发展了新的理论和方法。比如分形FSS，分形PBG，分形RFMEMS天线系统和分形馈电网络等。

时至今日，人类社会经济活动对地下水资源的破坏和危害越来越严重，而分形在岩石水力学中的应用也大显身手。文［6］以分形几何理论和岩体裂隙系统统计地质资料为基础，建立与描述岩体裂隙网络系统几何特性的分形模型。对岩体裂隙网络系统的分形几何结构进行研究，在物理本质上揭示了分形裂隙岩体水流动和溶质传输机理。常用的裂隙长度与裂隙数目的分形几何关系如下［7］：

式中N为裂隙的数目；c为常数，它表征了岩体的裂隙密度特性；dl为裂隙长度分形维数。同样，裂隙开度与裂隙数目的分形几何关系如下：

式中M为裂隙的数目，β为常数，dw为裂隙开度分形维数。文［8］基于分形理论、Monte Carlo模拟方法和修正的Hagen－Poiseulle方程以及Darcy定律，建立了多孔介质渗透率的分形解析表达式。Monte Carlo模拟结果与分形解析得到的渗透率进行了对比，两者具有良好的一致性，在多孔材料的热传导和渗流等方面取得了许多创新性的研究成果。文［9］研究了微孔道分形网络中热和气体传输特性，提出了多级分形网络的产生方法，建立了热传导参数和气体流动阻力的分形描述机理，指出其多孔介质的显微结构，包括孔径和孔隙界面，都显示出分形特征，我们把这些介质叫做分形多孔介质。目前已经证明，多孔介质的累积粒径分布（与工程表面的瑕点和地球上的岛屿等一样）遵循下面的分形标度律：

这里λ表示孔径，df为孔隙面积分形维数。同时也已经证实双向渗透的分散多孔介质是分形物体。不仅其粒子团簇是随机分布的，双向分散多孔介质中的大孔和微孔也是随机分布的（图3和4），图4是在双对数坐标中累积粒径数与孔径的关系，df＝1.80，等于该回归直线斜率的绝对值。

图3 累积粒径数与孔径关系图

图4 回归直线

文［10］提出了一种模拟三维裂隙中流体流动的方法，模型中采用了离散元和边界元方法，以便精确和有效地处理介质三维复杂的几何形状和非均质特性。文［11］基于分形理论和达西定律，研究了孔隙的弯曲分形维数和表面积分形维数与瓦斯渗透率参数之间的关系，数值模拟了煤层孔隙的弯曲分形维数和表面积分形维数对瓦斯渗透率参数的影响。这些研究成果不仅具有重要的理论价值，而且在工程中也具有实际应用意义。

2 在生物学和生命科学等领域中的应用

生物的生长尤其是微生物的生长形态极不规则，一般说来无法用正常的语言和用定量分析的方法来描述，而分形理论作为一种非线性几何学工具，使定量描述微生物生长成为可能。

文［12］论述了分形理论在植物根系研究方面的应用进展，以及利用分形维数研究植物根系分形特征的优越性，并对分形理论在植物根系研究领域的应用前景进行了展望。植物的根系结构是一个不规则的复杂结构，难以定量测定。分维数可以作为衡量根丰度的一个指标，分维数越大，植物根系分布就越均匀，且能反映植物生长能力的大小。与常规的研究方法相比，利用分形方法研究根系，具有工作量小、使用方便、精确度高的优点，是一种非常适合研究根系复杂性的方法。

如所知，分形理论是一个非线性科学分支，近年来它在形态学、生理学、生物化学、遗传学和病理学等方面都得到了广泛的应用。文［13］论述了血管网中分形问题的研究意义、内容、进展及其相应的基本理论与实验研究方法，重点评述了分形理论在血管网结构、血管生成和血管病理中的研究进展，以及血管网结构对肿瘤血管内物质输运的影响，分析了分形理论在血管网研究中的难点，并归纳了该领域内若干可供探索的途径和新方向。对血管网解剖结构显示，该系统有着非常不规则、粗糙的形式，且血管生成过程本质上是非线性的，以至于不能准确地应用传统的几何学方法来描述。

大量的实验发现血管网结构具有分形的特点，引入分形的方法来定量描述它们的特征，有利于联系和比较。血管网要同时满足分配和血液动力学两个功能。首先保证这个系统能达到它所服务的每一处组织或者器官，称为分配功能；其次是这个系统能够把血流速度降到足够低以使血液和单个细胞间代谢产物可充分交换，称为血液动力学功能。长期的探索，发现生物进化的结果是使血管网维持血流流动的能量最小，达到最优化。血管的分配功能必须使血管系统具有发达的分支结构。若每次分叉遵循同样的规律，则整个血管网有自相似性。由于每一血管段的直径和长度变化很大，且即使两个血管网分叉的次数相同，每一层的血管也会有很大的差别，这样基于分叉形成的自相似结构就变得不重要，也可以说不具备严格意义上的分形，而是一种伪分维。对称血管网主要是把血液均匀分布到周围组织，承担着分配作用。

人动脉血管中大多数血管都是非对称的。对称的分叉只在一部分小分支上出现，这也符合动脉血主要是给不同组织供血的实际情况。非对称血管网可使更多的血液输送到更长的路径。实际的血管网中都包括了这两种类型的血管分叉。如图5和6所示［14－15］。

图5 对称的血管组织

图6 不对称的血管组织

分形血管网复杂的几何解剖结构和关联流动的影响使得其内部的流动异常复杂，分叉分形网因与人体呼吸道相似很早就得到研究者的关注，其内的流动和传质都得到了充分的研究［16］。肿瘤血管网与正常组织血管网的几何结构有着显著性的差异，为使血管系统输运物质达到最优化，每一个组织单元里应该有一个最短血管路径的分维。肿瘤血管网的分维和最短血管路径的分维与正常组织血管网都有很大的区别。在其他疾病中血管网复杂性也会发生改变，因此其分维值有潜在的诊断价值。研究者发现严重糖尿病患者视网膜血管分布的分维值明显高于正常人，而在血管分布的分维值相同时，血管间隙分维的差异可以明确疾病的分形。除了血管病理以外，也有研究者尝试利用视网膜血管网分维作为一种身份检测识别方法。因此若能进一步证明人体视网膜血管网分维有特异性，将无疑是身份识别领域的一个重大突破。

分形理论是以局部的某些特征来解释整体，它为微生物的生长形态可以用分形维数来定量描述另辟蹊径。我们就可能对微生物的菌落分形、菌丝分形的现象和机制开展讨论，并认为环境因素，如土壤、水、恶劣环境和抗生素环境均可对微生物的分形产生影响。从而为在不同土壤团聚体粒径中微生物的分布特点研究找到相关基础。某些研究成果还介绍了计算机在微生物分形上的应用，指出了研究中有待解决的问题和与土壤科学相结合的研究方向［17－18］。

3 分形理论和多重分形分析应用于土壤地理学和岩石地质学的研究

众所周知，分形理论是一种描述高度复杂但具有标度不变性的非线性科学。土壤与岩石的成因与空间变异具有高度复杂性和随机性。分形理论在此领域内也大有用武之地。

利用分形理论，对土壤地理学可以进行定量分析［19］。该项工作基于总部设在罗马的联合国粮农组织和国际土壤学会的世界土壤资源报告，它指出把分形模型应用于欧洲的土壤表面系统进行科学研究是可行的。它首先研究并给出了土壤类别分布的幂律模型，及它们与土壤肥沃地区的关系；随后把覆盖于欧洲表面45种最丰富的土壤作为样本，计算了它们的分形维数，其范围限于3个数量级内。通过分析，揭示了一种土壤分布的标度行为，它足以证明分布在整个欧洲的土壤类别之分形特征，这些发现使人们认识到用分维数研究土壤类别，将给欧洲土壤体系的复杂性分析提供重要作用。

文［20］扼要综述了分形理论在土壤空间变异研究中的应用，着重讨论了利用矩方法计算土壤属性的分维数，介绍了利用多重分形分析法分析土壤空间变异的最新进展。总之，分形理论已经成为量化土壤属性空间变异性及尺度转换的重要工具。

文［21］以“用多重分形分析法确定玄武岩地质磁黄铁矿的微观结构”为题，探索与描述矿物颗粒的空间构造，确定矿物分布结构，模拟岩石的成因过程。从它们的切片和各种不同的模型即可判断矿物颗粒的几何特征和矿物排列的空间复合状态。

位于中国西南部云南省的个旧市锡多金属矿物的形成地是这项工作的考察点，该项目的目的是运用分形和多重分形方法量化确定磁黄铁矿颗粒的分布模式，其依据是7种玄武岩矿物截片样本所含的基本信息及其微量元素的含量，在环境控制扫描型电子显微镜下所得到的数字图像，如图7。

图7 环境控制扫描型电子显微镜下的数字图像

因为每幅图像中磁黄铁矿颗粒的界周和面积是分形可测（DAP）的，它们具有幂律关系，并具有标度不变性，可用多重分形分析和矩方法对磁黄铁矿颗粒的空间变异进行表征。从而可推断合理的玄武岩岩石学形成过程。在这方面，分形与多重分形分析将提供新发现，特别是在矿物微观结构的量化方面，也许它们与岩石块的地球化学分析所揭示的岩石发展学有着极其密切的关系。

4 地震学与分形

说到地震学与分形，其实在我们生活中最熟悉的一个现实原形就是岩石的分形概念。当岩石破碎时，破碎的岩石块的（等效）半径r和岩石块的数目N（≥r）之间存在着分形关系：

岩石是地质作用的产物，由一种或一种以上的矿物或岩屑组成的有规律的集合体。它是组成地壳和岩石圈的基本物质，如岩石圈中的花岗岩（图8）。

图8 岩石圈中的花岗岩

地球形成以来，在各种自然作用力下也象岩石一样不断有破裂过程发生，那么，地球介质是否也和岩石的分形一样，具有层次结构呢？地球物质不均一性的表现是多方面的。不同圈层间、同一圈层的不同构造层间、以及同一构造层内，它的化学不均一性都有所表现（图9）。地球内部划分为地壳、地幔和地核三个圈层。地壳主要由各种岩石组成，厚度各地有很大差异，大陆地区较厚，海洋地区较薄。地幔的深度从5～70km以下一直到2000km，地核分为二部分，地下2900～5000km深处，叫做外核，5000km以下的深部称内核。岩石圈是地球上部相对于软流圈而言的坚硬的岩石圈层。厚60～120km，为地震高波速带。包括地壳的全部和上地幔的上部，由花岗质岩、玄武质岩和超基性岩组成。地震的震源可以远远超过岩石圈的厚度。震源深度超过300km的，称为深源地震。目前世界上记录到的震源最深的地震是1934年6月29日发生于印度尼西亚苏拉威西岛东的地震，震源深度720km，震级为6.9级。深源地震常常发生在太平洋中的深海沟附近。在马里亚纳海沟、日本海沟附近多次发生了震源深度达五六百公里的大地震［22］。

图9 地球的内部结构

一个岩石层在移动时碰撞到另外一个岩石层时就会产生挤压和碰撞，当地下的岩层受力达到一定强度而发生破裂，就会出现地质断层，断层沿着破裂面有明显相对位置移动进而引发地震，就叫做断层型地震。根据岩层沿破裂面的位移方式，又可将断层分为正断层、逆断层和走滑断层。

较早的研究发现全球地震活动期间震级m以上的地震数目N（≥m）与震级m之间有如下关系式：

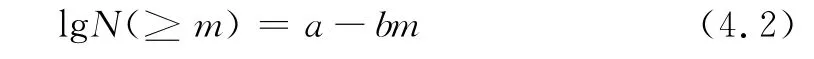
其中a，b为常数。（4.2）中的b值是一个重要参数，地震学家对此进行过深入研究。

据记载，1926～1986年日本东北地区所发生的大于5.5级的地震震中分布，求得其分维数d与b值的关系为d＝2.3－0.73b。地震学中，地震断层面面积A与地震矩M的关系为

μ是地震断层附近岩石的剪切模量（材料的一种力学性能指标），δ是地震时跨断层两侧的平均位移，它与断层面积有关。根据地震的错位模型，可把上式进一步表示为

其中r可看作地震的断层长度。衡量地震所释放的能量大小可以用地震震级和地震矩来表示。两者之间的关系为

一般情形下，上式中的c＝1.5和d＝9.7也是常数。把上面的4个式子联系起来可以导出

式中N（≥r）表示地震时断层长度不小于r的数目，Ar是个常参数。把c＝1.5代入上式，上式可写成

这表明，在一群地震中，发震断层长度和断层数目之间存在着幂律关系，即一群地震中，断层长度r的分布是分形的［23］。

目前关于地震的主要理论支撑是固体力学，因为地震从弹性能量的积累到突然释放，主要是一个力学过程。因此从力学角度进行研究是很自然的。但是在断层面上地震错动的理论模拟尚未在实用意义上展开，仍缺乏理论指导。如果能把经典的传统方法与分形理论相结合，无疑是有价值的。

（2011年11月1日收到）

［1］袁继红，袁群莉.分数维数的哲学启发 ［J］.长春师范学院学报，2002，21（2）：77－79.

［2］谢南瑞.多重碎形 ［J］.数学传播，1991，25（1）：27－32.

［3］JENSEN M H，KADANOFF L P，LIBCHABER A.Global universality at the onset of chaos：results of a forced Rayleigh－Bénard experiment［J］.Physical Review Letters，1985，55（25）：2798－2801.

［4］楚化强，郁伯铭.沸腾换热的分形分析 ［J］.力学进展，2009，39（3）：259－272.

［5］宋小弟，冯恩信，傅君眉，等.分形天线工程及其新进展 ［J］.无线通信技术，2008，（2）：48－54.

［6］于贺，李守巨，满林涛，等.岩体分形裂隙网络系统中水流动研究进展 ［J］.哈尔滨工业大学学报，2011，43（S1）：94－99.

［7］ZAZOUN R S.The fadnoun area，Tassili－n－Azjer，Algeria：Fracture network geometry analysis［J］.Journal of African Earth Sciences，2008，50（5）：273－285.

［8］YU B M，ZOU M Q，FENG Y J.Permeability of fractal porous media by Monte Carlo simulations［J］.International Journal of Heat and Mass Transfer，2005，48（13）：2787－2794.

［9］GHODOOSSI L.Thermal and hydrodynamic analysis of a fractal mirochannel network ［J］.Energy Conversion and Management，2005，46（5）：771－788.

［10］PERATTA A.A new scheme for numerical modeling of flow and transport process in 3D fractured porous media［J］.Advances in Water Resources，2006，29（1）：42－61.

［11］李守巨，刘迎曦.基于分形理论的煤层瓦斯渗透率参数估计方法 ［J］.西安石油大学学报，2007，22（2）：113－115.

［12］嵇晓雷，分形理论应用于植物根系形态分布的研究进展及其应用前景 ［J］.安徽农业科学，2010，38（25）：13693－13694.

［13］吕永钢，杨力.血管网分形研究进展 ［J］.化工学报，2010，61（12）：3051－3058.

［14］ZAMIR M.Fractal dimensions and multifractility in vascular branching［J］.Journal of Theoretical Biology，2001，212（2）：183－190.

［15］GABRYS E，RYBACZUK M，KEDZIA A.Fractal models of circulatory system.Symmetrical and asymmetrical approach comparison［J］.Chaos，Solitons and Fractals，2005，24（3）：707－715.

［16］PADAKI A，ULTMAN J S，BORHAN A.Ozone uptake during inspiratory flow in a model of the larynx，trachea and primary bronchial bifurcation ［J］.Chemical Engineering Science，2009，64（22）：4640－4648.

［17］罗红燕，蒋先军，谢德体.分形理论在微生物研究中的应用及展望 ［J］.微生物学杂志，2009，29（4）：75－78.

［18］BEN－JACOB E.Bacterial complexity：More is different on all levels［J］.Systems Biology，2009，1：25－35.doi：10.1007／978－4－431－87704－2＿3.

［19］IBÄÑEZ J J，PÉREZ－GÓMEZ R，SAN JOSÉMARTÍNEZ F.The spatial distribution of soils across Europe：a fractal approach［J］.Ecological Complexity，2009，6（3）：294－301.

［20］张法升，刘作新.分形理论及其在土壤空间变异研究中的应用［J］.应用生态学报，2011，22（5）：1351－1358.

［21］XIE S，CHENG Q，ZHANG S，HUANG K.Assessing microstructures of pyrrhotites in basalts by multifractal analysis［J］.Nonlin Processes Geophys，2010，17：319－327.doi：10.5194／npg－17－319－2010.

［22］王定华.地球的物质组成［M／OL］.［2011－02－28］.http：／／wenku.baidu.com／view／.

［23］陈颙，陈凌.分形几何学 ［M］.北京：地震出版社，2005：163－180.