“几何圆”在解决物理问题策略中的应用

费云霞

(湖州市南浔中学 浙江 湖州 313009)

在高三物理复习教学中，教师除了对高中物理内容做知识点的罗列和总结外，更注重培养学生的学习方法、思维能力，使学生在解决物理问题中掌握一定的策略，以习题中用到“圆”的思想为背景，谈谈对这一类问题的处理.

“ 圆”是平面几何中的重要图形，它有一些重要的特点可以帮助我们解决物理问题.在教学中, 教师应有意识地指导学生学会利用几何图形, 尤其是用“圆”处理问题, 从而提高学生运用几何知识解决物理问题的能力．

1 用“等时圆”解决物体下滑时间问题

在动力学问题中，常常会碰到讨论物体沿斜面下滑的时间问题，这个时间即跟斜面的倾斜程度有关，又跟斜面的长度有关，当这两者的关系可以用画圆来表示时，那么用圆的有关特点去解决问题就要方便很多．

【例1】如图1(a)所示，某轴承厂有一条滚珠传送带，传送带与水平面间的夹角为θ，上方A处有一滚珠送料口，欲使滚珠从送料口沿无摩擦的斜槽最快地送到传送带上，应采取的方法是

A．沿AB所在的竖直方向安放斜槽

B．过A点向传送带做垂线，得垂足C，就沿AC方向安放斜槽

C．应在AB和AC之间的某一适当位置安放斜槽

D．上述三种方法，滚珠滑到传送带上所用的时间相同

图1

解析:以AB为直径作圆，该圆必过C点，如图1(b)所示从A点随意取一条弦滑下，弦与竖直方向夹角为α，则

(1)

(2)

(3)

由三式联立可知，从A点沿不同光滑弦滑至圆周上各点的时间与从AB自由落体滑下的时间相等，所以此题滚珠从A到C和从A到B时间一样，而沿AB和AC之间的某斜槽到传送带的时间要少一点所以选C．

点评：此类型题目的原型是物体沿不同光滑斜面下滑的时间问题，斜面倾斜的角度越大，下滑的加速度就越大.但是到传送带的距离会变大，所以用公式法解决需要添加辅助线，问题会比较麻烦，利用圆就可以方便地解决问题，此类模型就是我们常说的“等时圆”模型．

2 用“矢量圆”解决矢量变化问题

在相互作用力这一章里，我们经常遇到在力系作用下，处于平衡的物体其所受诸力变化趋势判断问题．

【例2】如图2(a)所示，质量为m的小球，用一细线悬挂在点O处．现用一大小恒定的外力F(F﹤mg)慢慢将小球拉起，在小球可能的平衡位置中，问细线与竖直方向的最大的偏角是多少?

图2

解析：本题中研究对象小球可在一系列不同位置处于静止，静止时小球所受重力、细线上拉力及大小恒定的外力的合力总是为零．三力关系由一系列闭合的矢量三角形来描述，这些三角形中表示重力的矢量边是公共边，有一条矢量边长度不变，画出矢量三角形如图2(b)所示.

点评：物理问题中如果涉及到一个矢量的大小确定，方向待定时，可以利用圆把这个力所有可能性描述出来．在小船过河时，船速小于水速, 要想航程最短, 应如何过河的问题也要涉及到画圆求极值．

3 用“函数圆”计算玻璃的折射率

光学中做玻璃的折射率实验时，如果没有量角器或角度的三角函数值无法获得，那么用圆可以解决这个问题．

【例3】某学生在做“测量玻璃的折射率”实验时，作完光路图后，以O点为圆心，10.00 cm长为半径画圆，分别交线段OA、OO′连线的延长线于A和C点，过A点作法线NN′的垂线AB交NN′于点B，过C点作法线NN′的垂线CD交NN′于D点，如图3所示，没有量角器无法测角度，这位学生于是用刻度尺量得AB=6.00 cm，CD=4.00 cm，则该玻璃的折射率为多少．

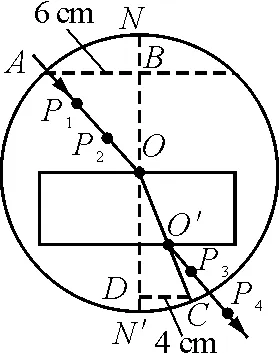
图3

解析:由题意可知入射角i=∠AOB，折射角r=∠COD，则由折射率公式

可解得

n=1.5

点评:上述实验数据处理方法是用直角三角形的边与边对应关系替代三角函数，避免了没有数学用表和量角器时无法计算的尴尬，由测角度转变为测线段长度，该题的命题者意在考查学生灵活处理实验数据的能力．

4 用“等势圆”解决电场中带电粒子做功问题

在电场章节中，抽象的概念比较多，“电势能”这一概念是学生学习的一个难点，而涉及到电场力做功的问题，也是高考的重点．

【例4】如图4(a)所示，直角三角形的斜边倾角为30°，底边BC长为2L，处在水平位置，斜边AC是光滑绝缘的，在底边中点O处放置一正电荷Q．一个质量为m、电荷量为-q的质点从斜面顶端A沿斜边滑下，滑到斜边上的垂足D时速度为v，该质点滑到非常接近斜面底端C点时，速度vC为多少，沿斜面向下的加速度aC为多少.

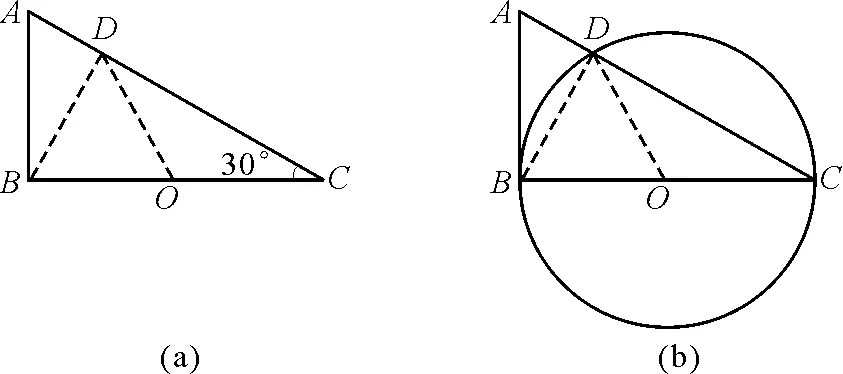
图4

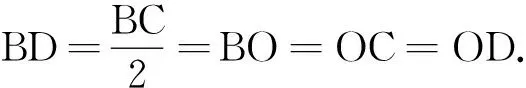
(4)

h=BDsin60°=BCsin30°sin60°

(5)

由式(4)、(5)得

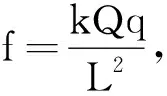
mgsinθ-fcosθ=maC

(6)

(7)

由式(6)、(7)得

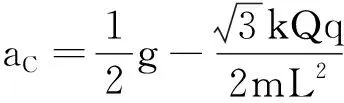
点评：在电场中，真空中静止点电荷产生的等势面是一个个的同心圆，而在等势面上任意两点间的电势差为零，在等势面上移动电荷电场力不做功，所以在点电荷产生的电场中计算电场力做功，可以用等效法画圆计算．

在电磁感应中，变化的磁场可以产生涡旋电场，与此相关的题目有时也要用到圆的相关特点．对于这类具体问题，可另做具体分析.

5 用“轨迹圆”解决磁场中带电粒子运动问题

带电粒子垂直进入匀强磁场区域, 在磁场区域内经历一段匀速圆周运动．既然轨迹是个圆的话，在解决此类问题时就有可能用到一些有关圆的特点．

【例5】如图5中虚线MN是一垂直纸面的平面与纸面的交线, 在平面右侧的半空间存在一磁感应强度为B的匀强磁场, 方向垂直纸面向外，O是MN上的一点, 从O点可以向磁场区域发射电荷量为+q、质量为m、速率为v的粒子,粒子射入磁场时的速度可在纸面内各个方向．已知先后射入的两个粒子恰好在磁场中给定的P点相遇,P到O的距离为L. 不计重力及粒子间的相互作用．求这两个粒子从O点射入磁场的时间间隔．

图5

解析：带正电q，速率v的粒子, 从O点垂直进入磁场，在洛伦兹力的作用下,做匀速圆周运动．因带电粒子射入磁场时速度方向可在纸面内沿各个方向, 画出带电粒子在此磁场中的轨迹，整图可能情况如图5所示，而先后射入的两个粒子恰好在磁场中给定的P点相遇, 这说明两粒子运动的轨迹是以OP为公共弦的两相交圆, 如图6所示.

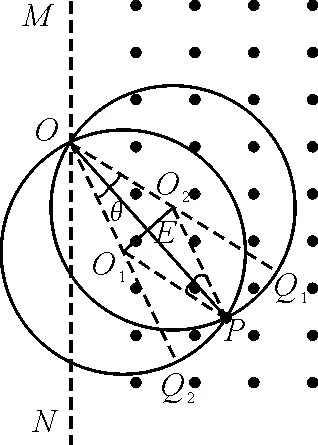
图6

(8)

(9)

(10)

由式(8)～(10)联立得

点评：带电粒子在匀强磁场中运动是高中物理的一个重点, 也是一个难点．因此, 如何指导学生掌握解决此类问题的解法很重要，而画圆是解决磁场中带电粒子运动的重要方法．在用圆解决磁场中粒子的运动问题时经常要用到一些圆的特点，比如圆心角与弧长的关系、垂径定理、相交圆定理、圆的内接四边形的性质定理、圆的对称性等．

参考文献

1 贾纪云. 圆在处理物理问题中的妙用.数理化学习，2006(Z1)

2 郑清俊，孙富贵.用圆的定理解物理问题.物理教师，2001：(9)

物理实验教学