高含水率吹填淤泥自然沉降规律

徐桂中, 吉 锋, 翁佳兴

(1. 河海大学 土木与交通学院， 江苏 南京 210098； 2. 东南大学 交通学院， 江苏 南京 210096)

随着港口、航道、海洋和海岸工程建设的飞速增多，我国每年都会开展大规模的清淤工程，因此会产生大量的疏浚淤泥。将疏浚出的淤泥吹填造地是目前处理疏浚淤泥最常用的方法，该方法不仅解决了疏浚淤泥处置难的问题，还为各种建设工程提供了大量的土源。由于国内疏浚以绞吸式为主，产生的疏浚淤泥的含水率往往极高，呈流体状态，在吹填场地中发生沉降。因此，了解吹填土的自然沉降规律对于合理进行吹填工程十分重要。

一般认为，沉降过程中，泥浆具有两种状态，即沉积状态与固结状态[1～7]。泥浆处于沉积状态时，土颗粒相互分离，土颗粒在重力和水的阻力作用下沉降，土颗粒的沉降规律可通过沉积理论描述[1, 8～10]；泥浆处于固结状态时，土颗粒相互接触并传递有效应力，土颗粒的下沉是由固结引起，土颗粒的下沉规律可运用大变形一维固结理论描述[11, 12]。有学者研究认为，沉积状态与固结状态之间存在临界含水率(浓度)，当含水率高于该临界含水率时，泥浆处于沉积状态，当含水率低于该临界含水率时，泥浆处于固结状态[13, 14]，该临界含水率往往被称为土形成含水率[15]。许多学者对土形成含水率开展了定量研究，Monnte 和Krizek认为土形成含水率在土的5.0～7.0倍液限之间[15]，Carrier等则认为土形成含水率为土的液限的7.0倍[16]，Stark等建立土形成孔隙比与塑性指数之间的关系[17]。

上述研究表明，泥浆的状态与含水率及土样的物理特性有关，然而，在疏浚工程中，泥浆的初始含水率却往往因原状土的特性及吹填机械的差异而变化，那么，泥浆的初始含水率的变化对自然沉积规律有何影响呢？此外，目前国内外对于定量确定土形成含水率尚未达到共识。针对上述问题，本文对中国4个地区的吹填淤泥开展室内自然沉降试验，探讨吹填淤泥的自然沉降规律及初始含水率、土的物理力学特性对自然沉降规律的影响。

1 土样的物理力学性质及试验方法

1.1 土样的物理力学性质

试验所用土样分别取自江苏淮安白马湖、江苏张家港、浙江温州、福建可门港等地。温州和可门港土样均由我国东海海相沉积形成，白马湖及张家港土样由河流沉积形成。张家港土样是用直径和高均为30 cm的PVC圆筒取于地下2.5米深度处，其它3种土样均为水力疏浚产生的疏浚淤泥。土样的基本物理指标见表1。其中，液限采用碟式液限仪测定，塑限采用搓条法测定，颗分采用密度计法测定，比重采用比重瓶法测定，试验过程严格按照GBT 50123-1999《土工试验方法标准》执行。图1显示了4种土样在塑性图中的位置，图中A线为IP=0.73(wL-20)，其中IP、wL分别为土样的塑性指数和液限。由图可知，张家港土样位于A线之下，属于粉质土，另外3种土样均位于A线以上，属于高液限黏性土。

表1 土样的基本物理力学指标

1.2 试验方法

试验所用的沉降容器为直径6.5 cm的1000 ml量筒，量筒外壁上附有精度为1 mm的刻度线，通过刻度线可以读取量筒中泥浆的高度。试验前，配置不同初始含水率的泥浆，并将配置好的泥浆缓慢注入量筒中，当泥面达到30 cm即停止注浆，并记录泥浆的初始高度。试验过程中，读取不同时刻泥面的高度；当泥浆沉积基本稳定后，终止试验，泥浆的初始含水率见表2。

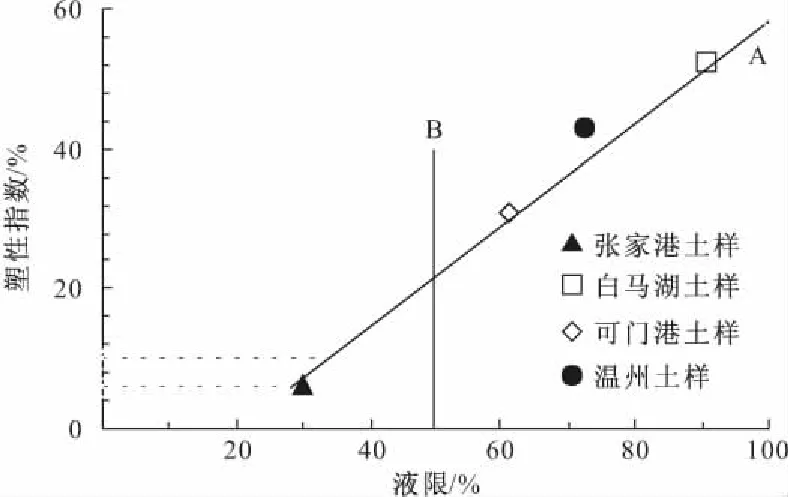
图1 塑性图

白马湖土样编号初始含水率%温州土样编号初始含水率%可门港土样编号初始含水率%张家港土样编号初始含水率%B1391W1325K1255Z163.1B2623W2671K2358Z280.8B3824W3738K3499Z398.0B4894W4843K4561Z4179.5B5960W5890K5781Z5242.2B61063W61095K61296Z6455.5B71280W71291K71751B81291W81679K82120B91997W91921

2 试验结果与分析

2.1 泥面沉降规律

由于试验初期的泥面变化较大，所以为了能够清楚了解试验初期的泥面沉降规律，图2中给出了4种土样自然沉降开始后1500 min(约1 d)内的沉降曲线。由图2可知，泥面的沉降规律受到初始含水率的影响，当初始含水率较低时，泥面沉降缓慢，如图2中B1、B2、B3、W1、W2、K1、K2、K3、Z1、Z2、Z3； 当初始含水率较高时，如除B1、B2、B3、W1、W2、K1、K2、K3、Z1、Z2、Z3之外的其他曲线,沉降曲线明显可分为3个阶段，泥面在短时间内保持基本平衡后快速沉降，沉降速率相等，而后泥面的沉降速率又迅速降低至初始含水率较低时的沉降速率。

图2 试验初期的沉降曲线

图3 整个试验期间的沉降曲线

图3为在半对数坐标系中泥面的沉降曲线，通过该图可以了解整个试验期间，泥面的沉降规律。图中显示，当初始含水率较高时，沉降曲线的曲率发生了显著的突变，而当初始含水率较低时，曲线形状与常规压缩试验中s-lgt曲线相似，呈明显的反“S”形。

图4 沉降曲线分类

上述现象表明，随着初始含水率的变化，泥浆的沉降曲线可分为如图4所示的I、II两种类型。分析认为，I、II之间的差别是由泥浆的初始状态不同引起。曲线I的形状与常规压缩试验中s-lgt曲线相似， I发生的条件为泥浆的初始状态为固结状态。

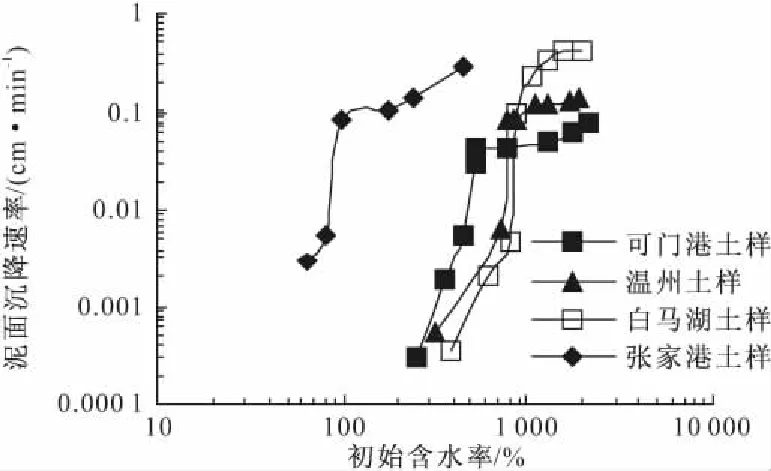
图5 试验初期泥面沉降速率随初始含水率的变化规律

图5为试验初期，泥面的沉降速率随初始含水率的变化关系，对于I型曲线为1500分钟内的平均沉降速率，II型的为泥面等速率下沉时的斜率。图中显示，II型发生时，泥浆的沉降速率显著大于I型，并且沉降速率随初始含水率的增大呈双折线型增大，表明随着沉降类型由I向II转变时，泥面沉降速率随初始含水率的变化规律也发生了变化。由此也可以推断，II发生的条件为泥浆的初始状态为沉积状态。为了叙述方便，分别将I、II两种沉降类型称为沉积沉降与固结沉降。

2.2 沉积沉降

当泥浆的初始状态为沉积状态时，泥浆发生沉积沉降，下面对沉积沉降的过程进行简述。水中的土颗粒受到自重及水的阻力的影响，当土颗粒受到的重力小于水的阻力时，土颗粒悬浮运动，否则，土颗粒下沉。由于细颗粒土具有絮凝作用，所以在土颗粒做悬浮运动的同时，相互絮凝成絮团，絮团又相互絮凝成更大的絮团，重量增加。当絮团的重量小于水的阻力时，絮团仍悬浮在水中，当絮团的重量大于水的阻力时，絮团下沉，泥面开始沉降。由此可见，沉积沉降时，泥面保持短暂的稳定，与土颗粒的絮凝相关[2]。将泥面保持稳定的时间称为絮凝时间，图6为絮凝时间随初始含水率的变化关系，由图可知，白马湖土样与温州土样的絮凝时间随初始含水率的增加而非线性降低。可门港土样与张家港土样中絮凝时间为0，表明沉降曲线中没有明显的絮凝现象。由此可见，泥浆的絮凝与初始含水率及土性相关，对于液限较高的土样，絮凝时间随含水率的增大而降低，液限较低的土样，絮凝现象不明显。

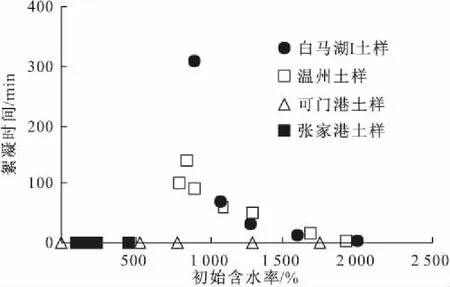
图6 絮凝时间随初始含水率的变化规律

在泥浆沉积过程中，泥面等速率沉降的现象已被许多学者通过实验所证实，这是由于沉积过程中土颗粒(絮团)相互影响，羁绊群体下沉引起，这种沉降形式被称为阻碍沉降(Hinder settling)[1, 2, 9]。研究表明，阻碍沉降发生时，土的初始骨架尚未形成，泥浆处于流态，土颗粒相互分离，由于土颗粒间的相互影响，土颗粒在自重的作用下相互羁绊下沉，泥面表现为等速率沉降，由此可见，沉积沉降中发生等速率下沉的原因在于泥浆发生了阻碍沉降。结合图5可知，泥浆发生阻碍沉降时，沉降速率随初始含水率的增大而增大；相同初始含水率时，沉降速率由大到小依次为张家港土样、白马湖土样、温州土样、可门港土样，表明相同含水率时，粉质土的阻碍沉降速率大于黏性土；对于黏性土，相同初始含水率时，阻碍沉降速率随土样液限的增加而增加。

泥浆发生阻碍沉降的同时，下沉至底部的土颗粒相互堆积，形成松散的土，此时土颗粒相互接触并可以传递有效应力；由于自重的影响，土体内产生超孔压，随着超孔压的消散，有效应力增加，土体固结下沉。在此期间，整个泥浆被分为上下两个区域，上部泥浆仍发生阻碍沉降，下部泥浆则进入固结状态。为描述方便，将上述两个区域间的界面称为土形成面。随着泥浆中土颗粒的不断下沉，泥面不断下降，土形成面不断上升，当所有土颗粒在底部堆积时，泥浆完全进入固结阶段，泥面的沉降速率迅速降低，并在自重固结作用下沉降。显然，沉积沉降时，泥面等速沉降段和慢速沉降段分别由泥浆的阻碍沉降和自重固结引起。由此可见，泥浆的沉积过程可分为3个阶段，即絮凝阶段、阻碍沉降阶段、自重固结阶段，如图7所示。

图7 沉积沉降时泥浆沉降过程示意简图

2.3 定量确定土形成含水率

泥浆进入固结状态时的含水率即为土形成含水率，用w*表示。据上所述，当初始含水率大于土形成含水率时，土样发生沉积沉降，否则，泥浆发生固结沉降。由此可见，土形成含水率必然介于泥浆发生沉积沉降和固结沉降的初始含水率之间，即可以通过泥浆的沉降类型定量判断土形成含水率。方便起见，将初始含水率与土样液限的比值称为相对初始含水率。图8中显示了各组试验的相对含水率，图中空心圆表示发生了沉积沉降，实心圆表示发生了固结沉降。因为土形成含水率必然位于空心圆与实心圆的交汇处，所以根据图8可以粗略定量了解4种土样的土形成含水率。由图8可知，对于白马湖土样、温州土样、可门港土样3种黏性土，土形成含水率约为液限的9倍，图8中实线所示，而张家港土样的土形成含水率约为液限的3倍，在图8中，位于实线的下方。

图8 本次试验4种土样的相对初始含水率

Carrier对美国地区疏浚淤泥堆场进行调查后，认为土进入自重固结时的临界含水率为液限的7倍[16]，该结论明显小于本文中的9倍液限，见图8。分析认为，这是由确定泥浆进入固结状态的临界含水率的方法不同引起。Carrier是在沉积稳定后，测定泥浆表面的含水率来确定泥浆进入固结状态的临界含水率的，然而这种方法必然需要取一定重量的表面泥浆，所以无法避免取样的泥浆已经在沉积过程中发生了自重固结，导致测定的临界含水率低于实际的临界含水率，本文的方法不存在上述问题。

2.4 自然沉降稳定时间

一般认为，在s-lgt坐标系中，沉降曲线趋于水平时，泥浆内超孔压消散完毕，泥浆自重固结完成，标志自然沉降结束[8]，将自然沉降结束所需的时间称为沉降稳定时间，并用Tc表示。在吹填工程中，吹填土的沉降稳定时间是堆场容积设计的重要参考指标。图9为Tc与相对初始含水率的关系，图中显示，4种土样，Tc均随相对初始含水率的增加呈非线性降低趋势。相同相对初始含水率时，白马湖、温州、可门港3种黏性土样的Tc相互接近，并且均符合式(1)所示的关系，由式(1)可知，Tc随土样的液限的增加而增加。然而，张家港土样的Tc则位于式(1)所示关系的下方，表明粉质土的沉降稳定时间显著小于黏性土。分析认为，上述现象与各土样的渗透性相互差异相关，土样的渗透性越好，自然沉降稳定所需的时间越小。相对初始含水率越高，土样的孔隙比越大，渗透性越高，所以沉降稳定时间越小。对于黏性土，液限越高，渗透性越低，所以Tc随液限的增加而增加，而粉土的渗透性显著优于黏性土，所以张家港土样的Tc显著低于其它3种黏性土。

图9 Tc随相对初始含水率的变化关系

(1)

3 结 论

(1)当泥浆的初始含水率大于土形成含水率时，泥浆在试验的初始时刻处于沉积状态，泥浆发生沉积沉降；当泥浆的初始含水率小于土形成含水率时，泥浆在试验的初始时刻处于固结状态，泥浆发生固结沉降。

(2)沉积沉降发生时，泥浆经历絮凝、阻碍沉降、自重固结3个阶段，对于液限较低的土样，沉积沉降曲线中没有明显的絮凝现象。泥浆发生阻碍沉降时，沉降速率随初始含水率的增大而增加；相同含水率时，粉质土的沉降速率大于黏性土的，对于黏性土，沉降速率随土样液限的增加而增加。

(3) 土形成含水率与土样的液限相关，黏性土的约为液限的9倍，粉质土的约为液限的3倍。

(4) 由于渗透性的差异，沉降稳定时间随相对初始含水率的增大非线性减小，随液限的增大而增大，黏性土的沉降稳定时间可以通过式(1)描述，并且显著大于粉质土的。

[1] Kynch G J. A theory of sedimentation[J]. Transactions of Faraday Society, 1952, 48: 166-176.

[2] Imai. Setting behabior of clay suspension[J]. Soil and Foundation, 1980, 20(2): 61-77.

[3] 吴正友. 连云港吹填泥浆沉积和固结性质的现场观测与分析[J]. 水运工程, 1990, (4): 1-6.

[4] 刘 莹, 肖树芳, 王 清. 吹填土室内模拟试验研究[J]. 岩土力学, 2004, 25(4): 518-521.

[5] 刘 莹, 王 清. 吹填土沉积后微观结构特征定量化研究[J]. 水文地质工程地质, 2006,(3): 124-127.

[6] 詹良通, 童 军, 徐 洁. 吹填土自重沉积固结特性试验研究[J]. 水利学报, 2008, 39(2): 201-205.

[7] 杨爱武, 杜东菊, 赵瑞斌, 等. 吹填泥浆沉积模拟试验研究[J]. 辽宁工程技术大学学报(自然科学版), 2010, 29(4): 617-620.

[8] Imai. Experimental studies on sedimentation mechanism and sediment formation of clay materials[J]. Soils and Foundations, 1981, 21(1): 7-20.

[9] Been K, Sills G C. Self-weight consolidation of soft soils: an experimental and theoretical study[J]. Géotechnique, 1981, 31(4): 519-535.

[10] Tan T S, Yong K Y, Leong E C, et al. Sedimentation of clayey slurry[J]. Journal of Geotechnical Engineering，ASCE, 1990, 116(6): 885-898.

[11] Gibson R E, England G L, Hussey M J L. The theory of one-dimensional consolidation of saturated clays:Ⅰ. finite non-linear consolidation of thin homogeneous layers[J]. Geotechnique, 1967, 17: 261-273.

[12] Toorman E A. Sedimentation and self-weight consolidation: general unifying theory[J]. Geotechnique, 1996, 46(1): 103-113.

[13] Monte J L, Krizek R J. One-dimensional mathematical model for large-strain consolidation[J].Geotechnique, 1976, 26(3): 495-510.

[14] Sills G C.Time dependent processes in soil consolidation[C]// Proceedings of the international symposium on compression and consolidation of clayey soils, IS-Hiroshim.rotterdam: A A. Balkema. 1995: 875-890.

[15] Pane V, Schiffman L. The permeability of clay suspensions [J]. Géotechnique, 1997, 47(2): 273-288.

[16] Carrier W D III, Bromwel L G, Somogyi F. Design capacity of slurried mineral waste ponds[J]. ASCE J. Geotech Engng, 1983, 109(5): 699-761.

[17] Stark T D, Choi H, Schroeder P R. Settlement of dredged and contaminated material placement areas.II: Primary consolidation，secondary compression，and desiccation of dredged fillinput parameters[J]. Water Port Coastal Ocean Engng, 2005, 131(2): 52-61.